
Лекции / SKD_Lektsia_12_-_Kolebania_materialnoy_tochki
.pptx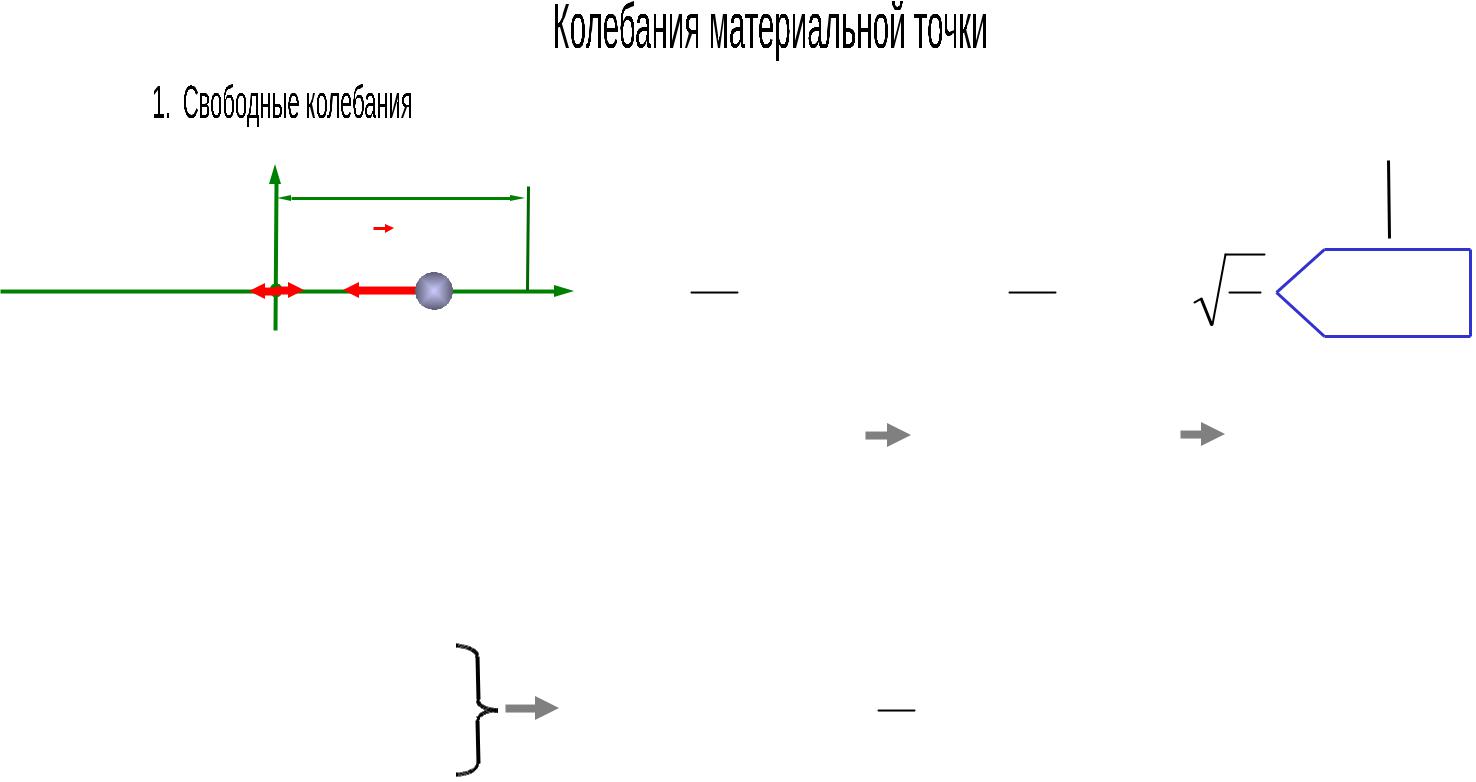
|
|
y |
x(t) |
|
F c x; |
mx F ; |
|
|
|
m |
||||||||||||
|
|
|
F |
|
|
|
c |
|
|
|
|
|
|
|
|
c |
|
|
mx cx 0 |
|
||
|
|
O |
|
x |
x 0; k |
2 |
|
|
|
; |
k |
c |
круговая |
|||||||||
|
|
|
x |
|
|
|
|
|
|
|
m |
колебаний |
||||||||||
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
m |
|
|
|
частота |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
|
|
|
|
|
|
t |
|
|
|
2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||
x k |
|
|
– дифференциальное уравнение свободных колебаний материальной точки. |
|
||||||||||||||||||
|
x 0Решение ищем в виде: |
|
x e |
|
; |
|
|
k |
|
0; |
k i; |
|||||||||||
бщего решения: |
x C1 cos kt C2 sinkt |
|
x C1k sinkt C2k cos kt. |
|||||||||||||||||||
сновная форма |
|
|
|
|
|
|
|
|
|
x x0 |
x v0 |
|
|
|
||||||||
пределение констант: Начальные условия: при |
|
t 0 |
|
|
|
|
||||||||||||||||
|
|
: |
|
|
|
|
|
, |
|
|
. |
|
|
|
||||||||
x0 C1 C2 0; |
C |
1 |
x ; C |
2 |
v0 . |
|
|
|
|
|
|
|
|
|
|
|||||||
v0 C1k 0 C2k; |
|
|
0 |
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
cos kt v0 sinkt |
||||||||||
Частное решение дифференциального уравнения |
x x |
|
||||||||||||||||||||
свободных колебаний материальной точки в |
|
|
|
|
|
0 |
|
|
|
|
k |
|
|
|||||||||
основной форме: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
t |
|
2 |
|
2 |
|
|
|
|
|
– дифференциальное уравнение свободных колебаний материальной точки. |
||||||||
x k |
|
x 0Решение ищем в виде: |
x e ; |
|
|
k |
|
0; |
|
k i; |
|
|
|
|
|||||||
|
|
|
|
|||||||
мплитудная форма |
|
|
или |
x A sin cos kt Acos sinkt. |
|||||||||||||||
бщего решения: |
|
|
|||||||||||||||||
x A sin kt |
|
|
|
|
x C1 cos kt C2 sinkt |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
C1 A sin ; C2 Acos . |
|||||||||||
|
|
|
|
|
|
|
|
v2 |
|
|
|
|
|
|
|
|
|
|
|
А – амплитуда колебаний: A C 2 |
C 2 |
x2 |
; |
|
|
|
|
|
|
|
|
|
|||||||
|
0 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
1 |
2 |
|
0 |
|
k2 |
tg C1 |
kx0 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
; |
|
|
|||||||||
α – начальная фаза колебаний (изменяется в пределах [0,2π]): |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
C |
2 |
v |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Частное |
решение дифференциального уравнения |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
x2 |
v0 |
|
|
|
|
kx0 |
|||||||||
свободных |
колебаний |
материальной |
точки в |
|
x |
|
|
|
sin kt |
arctg |
|
||||||||
|
|
|
|
||||||||||||||||
амплитудной форме: |
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
v0 |
||
|
|
|
|
|
|
|
0 |
|
2 |
|
|
|
|
|
|
|
|||
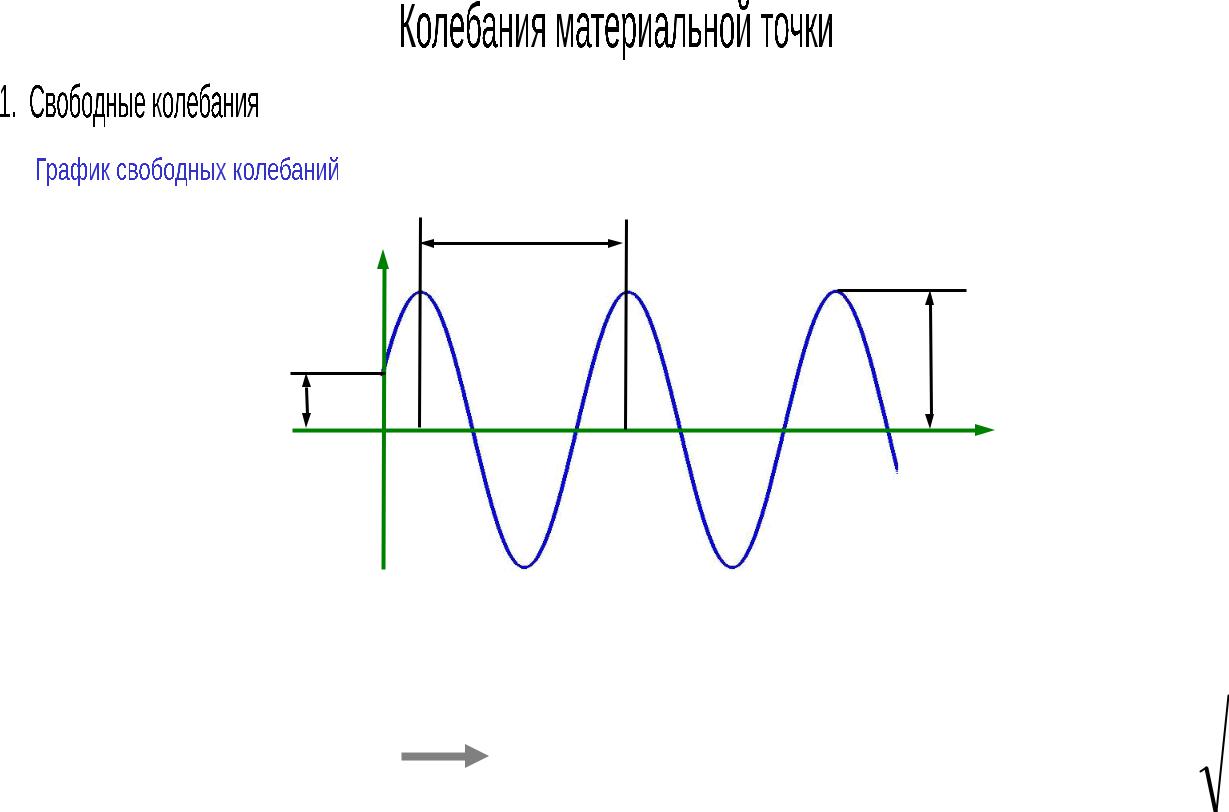
Т – период колебаний.
x
A – амплитуда колебаний.
начальная фаза |
x0 |
|
колебаний |
O |
t |
|
ериод колебаний: Значение периода колебаний получается из условия, по которому добавление периода к переменной изменяет фазу колебаний на наименьший период для синуса – 2π.
|
|
|
2 |
|
|
|
|||||
k t T kt 2 ; |
T |
Для прямолинейных |
T 2 |
m |
|||||||
k |
C |
||||||||||
1 |
|
k |
|
|
|
колебаний точки: |
|
||||
|
|
|
|
|
|
|
|||||
|
|
|
k 2 . |
|
|
||||||
|
|
|
|
– частота колебаний (Гц); |
|
|
|||||
T |
2 |
|
|
||||||||
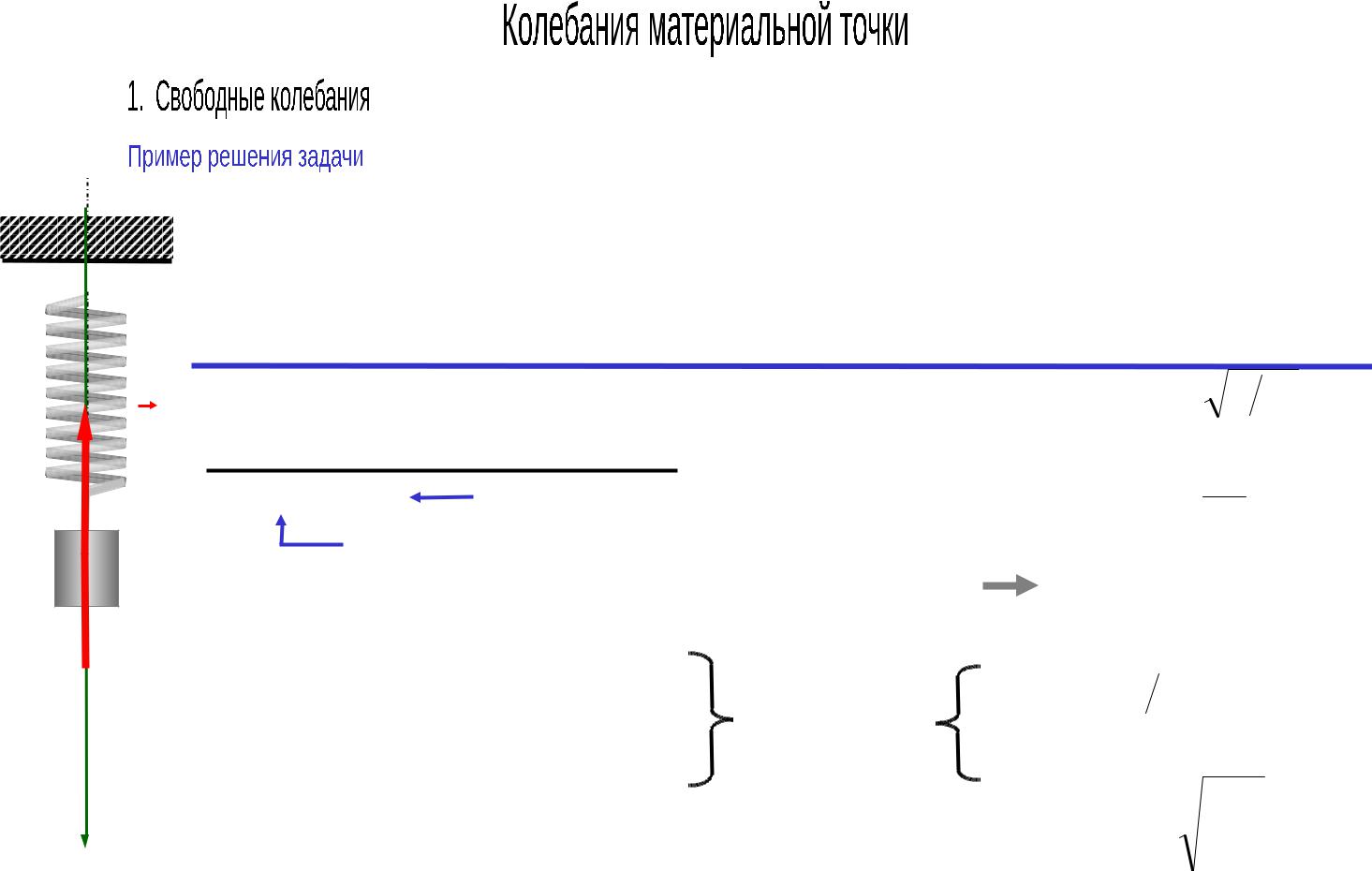
 A
A
F
B  y
y
C

P

x
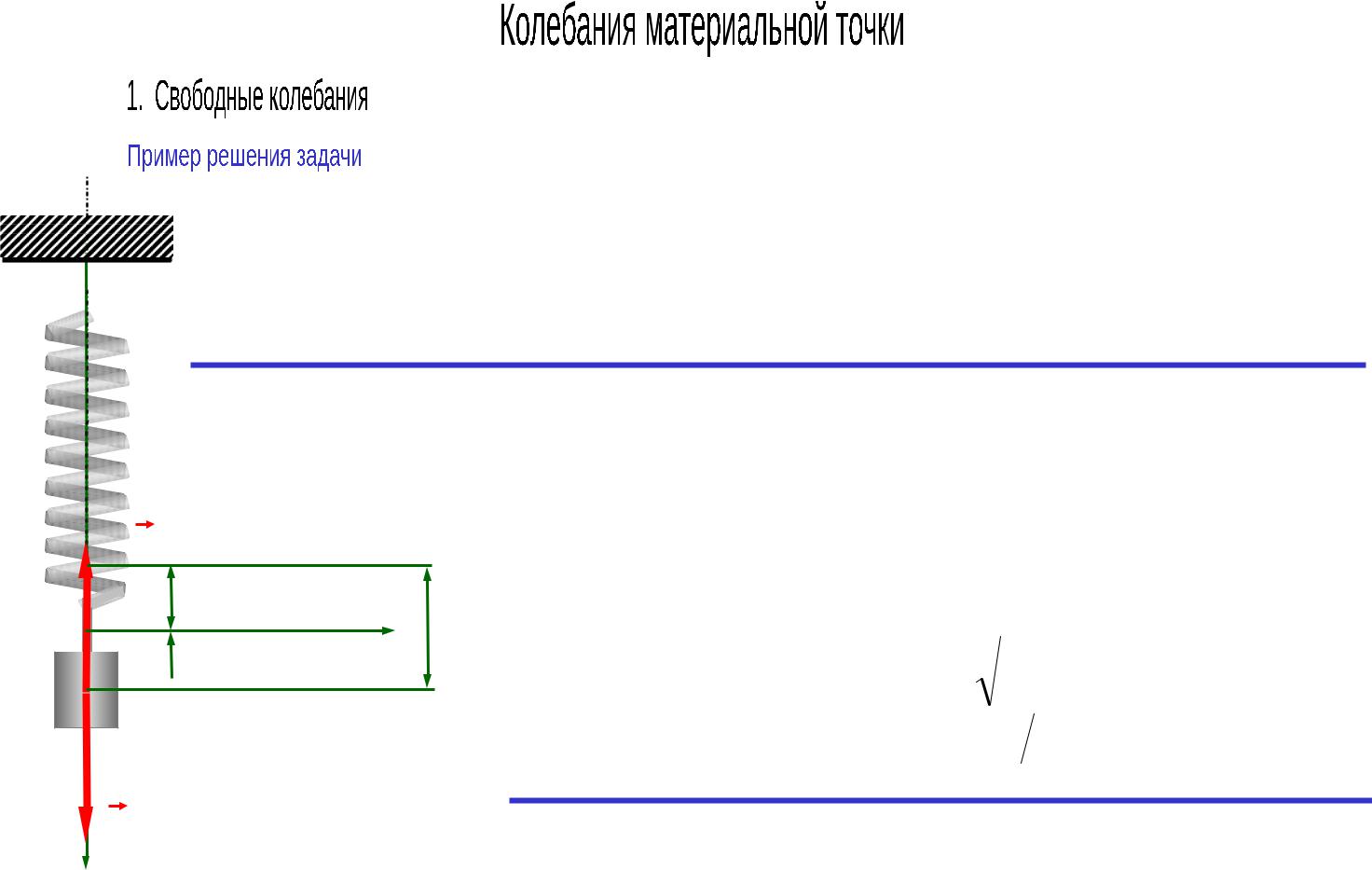
Пружина АВ, закрепленная одним концом в точке А, имеет жесткость с = 19,6 н/м. В некоторый момент к нижнему концу В недеформированной пружины подвешивают гирю С массой m = 0.1 кг и отпускают ее без начальной скорости.
Найти уравнение движения гири, амплитуду и период ее колебаний пренебрегая массой пружины.
|
|
|
|
|
ma P F ; |
|
mx mg F ; mx mg cx; k c m ; |
|||||||||
Решение: |
x k |
2 |
x g |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
– дифференциальное уравнение движения гири. |
mg ; |
|||||
x x1 x2 ; |
|
частное решение неоднородного дифуравнения: x2 g |
||||||||||||||
|
|
|
|
|
общее решение однородного дифуравнения: x |
k2 x 0; |
k2 |
c |
||||||||
|
|
C |
|
|
характеристическое уравнение: 2 k2 01 |
|
1 ki; |
|
|
|||||||
x |
1 |
1 |
cos kt C |
2 |
sinkt. |
|
начальные условия: при |
t 0 :x0 |
|
|
||||||
|
|
|
|
|
|
|
|
mg |
0;x0 0. |
|||||||
x C1 cos kt C2 |
sinkt |
определение |
C1 mg c ; |
|
|
|||||||||||
c |
произвольных |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
C2 0. |
|
|
|||
x C1k sin skt |
C2k cos kt |
постоянных: |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x mg cos |
mg t mg |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
c |
c |

|
A |
C |
BF |
|
λст |
|
x |
Пружина АВ, закрепленная одним концом в точке А, имеет жесткость с = 19,6 н/м. В некоторый момент к нижнему концу В недеформированной пружины подвешивают гирю С массой m = 0.1 кг и отпускают ее без начальной скорости.
Найти уравнение движения гири, амплитуду и период ее колебаний пренебрегая массой пружины.
Решение: ma P F . В положении статического равновесия: 0 P F ;
|
F c ст |
|
ст P c mg c |
|
|
|
||||
движения |
|
mx mg F ; mx mg c x ст ; |
||||||||
начало |
|
|
|
|
|
|
|
|
|
|
|
|
x mg k x mg; |
|
|
|
|||||
деформация |
|
k |
c m 14; |
|||||||
|
|
|
|
2 |
|
|||||
статическая |
x+λст |
|
|
|
|
|
|
|
||
положение y |
|
|
2 |
|
|
|
|
|
||
деформация |
|
|
|
|
|
|
|
|||
статического |
|
|
|
|
|
|
|
|||
пружины |
x k |
x 0 |
– дифференциальное уравнение |
|||||||
равновесия |
|
|||||||||
|
|
|
движения гири. |
|||||||
P |
Характеристическое уравнение: 2 k2 0 |
ki. |
x |
Общее решение однородного дифуравнения: |
x C1 cos kt C2 sinkt |
P |
|
 A
A
F
B 
λст
 x C
x C

Пружина |
АВ, закрепленная одним концом |
в точке А, имеет жесткость с = |
|||||||||
19,6 н/м. В некоторый момент к нижнему концу В недеформированной пружины |
|||||||||||
подвешивают гирю С массой m = 0.1 кг и отпускают ее без начальной скорости. |
|||||||||||
Найти уравнение движения гири, амплитуду и период ее колебаний пренебрегая |
|||||||||||
массой пружины. |
|
|
|
|
|
|
|
|
|
||
Решение: |
x C1 cos kt C2 sinkt |
x C1k sin skt C2k cos kt; |
|||||||||
|
|||||||||||
Начальные условия:при t 0 : x0 ст ; x0 |
0. |
|
|
0. |
|||||||
Определение произвольных постоянных: C |
1 |
|
0,05; |
C |
2 |
||||||
начало |
|
|
|
ст |
|
|
|
|
|||
движения |
|
x 0.05 cos 14 t |
м – уравнение движения гири. |
||||||||
деформация |
|
||||||||||
статическая |
x+λст |
|
|
|
|
|
|
|
|
|
|
положение y |
|
|
|
|
|
|
|
|
|
||
деформация |
Амплитуда колебаний: A C1 C2 |
0.05 м. |
|||||||||
статического |
пружины |
||||||||||
|
|
|
|
2 |
2 |
|
|
||||
равновесия |
|
|
|
|
|
|
|
|
|
|
|
|
|
Период колебаний: |
T 2 k 0.45 c. |
||||||||
x |
|
x 0.05 cos 14 t м; A 0.05 м; |
T 0.45 c. |
P |
Ответ: |
|
|
y |
x(t) |
|
|
F c |
x; R |
|
mx |
R F ; |
m |
|||
|
F |
|
|
x; |
|
|||||||
O |
|
|
|
|
|
c |
|
|
c |
|
|
|
|
|
|
|
|
|
2 |
|
|||||
|
|
|
x |
|
|
|
|
|||||
|
|
|
|
|
|
|
x 0; k |
|
; 2n ; |
|||
|
R |
R |
|
x |
|
x |
|
|
||||
|
|
|
m |
|
m |
|
|
m |
|
m |
||
|
|
|
|
|
|
|
|
|||||
x 2nx k |
2 |
x 0 |
– дифференциальное уравнение затухающих |
|
|
||||
|
|
|
|
|
колебаний материальной точки. |
|
|
||
ешение ищем в виде: |
x e t ; |
2 2n k2 0; |
|
n |
n2 k2 ; |
||||
|
|||||||||
|
|||||||||
Три случая решения дифференциального уравнения:
1.Случай малого сопротивления:
2.Предельный случай:
3.Случай большого сопротивления:
n k;
nk;
nk;

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,2 n k1i, |
|
|
|
|
|
|
|
|
|
|
|
2 |
круговая частота |
||||
|
|
2 |
|
2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
k1 k |
|
n |
|
|
|
|
mc 2m |
|
Затухающих колебаний |
||||||||
|
|
где |
|
|
|
|
|
||||||||||
Основная форма общего решения: |
x e nt C1 cos k1t C2 |
sink1t |
|||||||||||||||
|
nt |
C1 cos k1t C2 sink1t e |
nt |
C1k1 sink1t C2k1 cos k1t . |
|||||||||||||
x ne |
|
|
|
|
|
||||||||||||
пределение констант: Начальные условия: при |
|
t 0 : x x0 , x v0 . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
x0 1 C1 C2 0 ; v0 nC1 C2k1 ;
Частное решение дифферен- циального уравнения затухающих колебаний материальной точки в основной форме:
C |
1 |
x ; |
C |
2 |
|
1 |
v nx . |
|
|
||||
|
|
|
|||||||||||
|
|
0 |
|
|
k1 |
|
0 |
|
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x e nt x |
cos k t |
1 |
v |
nx |
sink t |
|
|||||||
|
|
||||||||||||
|
|
|
0 |
|
|
1 |
|
0 |
0 |
1 |
|||
|
|
|
|
|
|
|
|
|
k1 |
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
|
n k |
|
|
|
|
|
||
мплитудная форма |
x Ae nt sin k t |
|
|
|
|
|
|
|
|
|
|
|||||||||
бщего решения: |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
ли x e nt A sin cos k t Acos sink t |
. C |
A sin ; |
|
|||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
C12 Acos . |
|
|||||
x e nt C1 cos k1t C2 sink1t |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
v |
nx |
2 |
|
|
|
|
|
|
|
Амплитуда колебаний: A C |
2 |
C |
2 |
|
|
x |
|
|
|
|
|
|
|
|||||||
1 |
2 |
|
|
0 |
0 |
; |
|
|
|
|
|
|
||||||||
|
|
|
|
|
0 |
|
|
k2 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
C1 |
|
|
x0k1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
α – начальная фаза колебаний (изменяется в пределах [0,2π]): tg C |
|
|
|
|
|
; |
||||||||||||||
2 |
v |
nx |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
|
|
||
Частное решение дифферен- циального уравнения затуха- ющих колебаний материальной точки в амплитудной форме:
x |
x2 v0 |
nx0 |
2 |
sin kt arctg |
|
x0k1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
0 |
k2 |
|
|
|
|
|
|
|
v |
nx |
||||
|
|
1 |
|
|
0 |
0 |
|
n k
|
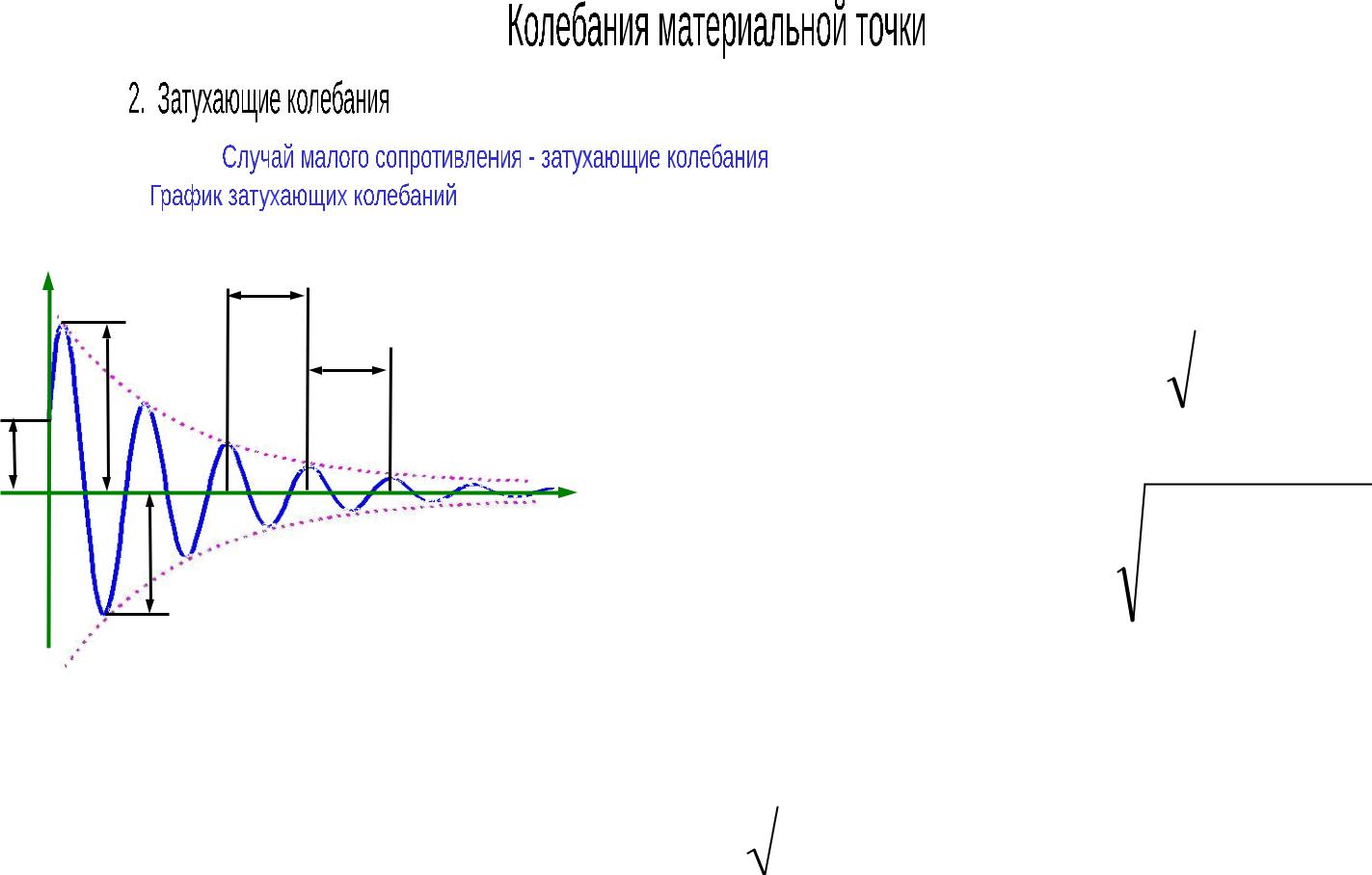
Т1 |
|
x0 – начальная фаза колебаний; |
x |
|
T – период колебаний; |
|
|
|
||
A1 |
e nt |
Т1 |
A1 , A2 – амплитуда колебаний; |
|
|
|
Условный период колебаний (c):
T |
2 |
|
|
|
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
1 |
k1 |
|
|
|
m |
2m |
|
|||
|
|
|
|
c |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Частота колебаний (Гц):
O |
|
|
|
t |
|
|
|
|
e nt |
|
|
|
|
|
|
|
|
|
|
|
|
||
A2 |
|
|
|
|
|
|
|
|
|
D |
A1 |
e |
nT |
; |
|
Декремент затухания: |
2 |
|
|||||
A |
|
|
|||||
|
|
|
|
|
|
||
|
|
2 |
|
|
|
nT |
|
Логарифмический |
|
ln D |
|
||||
декремент затухания: |
2 |
||||||
|
1 |
|
k |
|
1 |
|
c |
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
T1 |
2 |
2 |
|
m |
2m |
|||||
|
|
|
|
|
|
|
|
|
|
Добротность: Q |
k |
|
|
|
2n |
||
|
|
|
|||
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
Q2 0.25 |
|
|
|
