
Лекции / SKD_Lektsia_05_-_Trenie
.pptx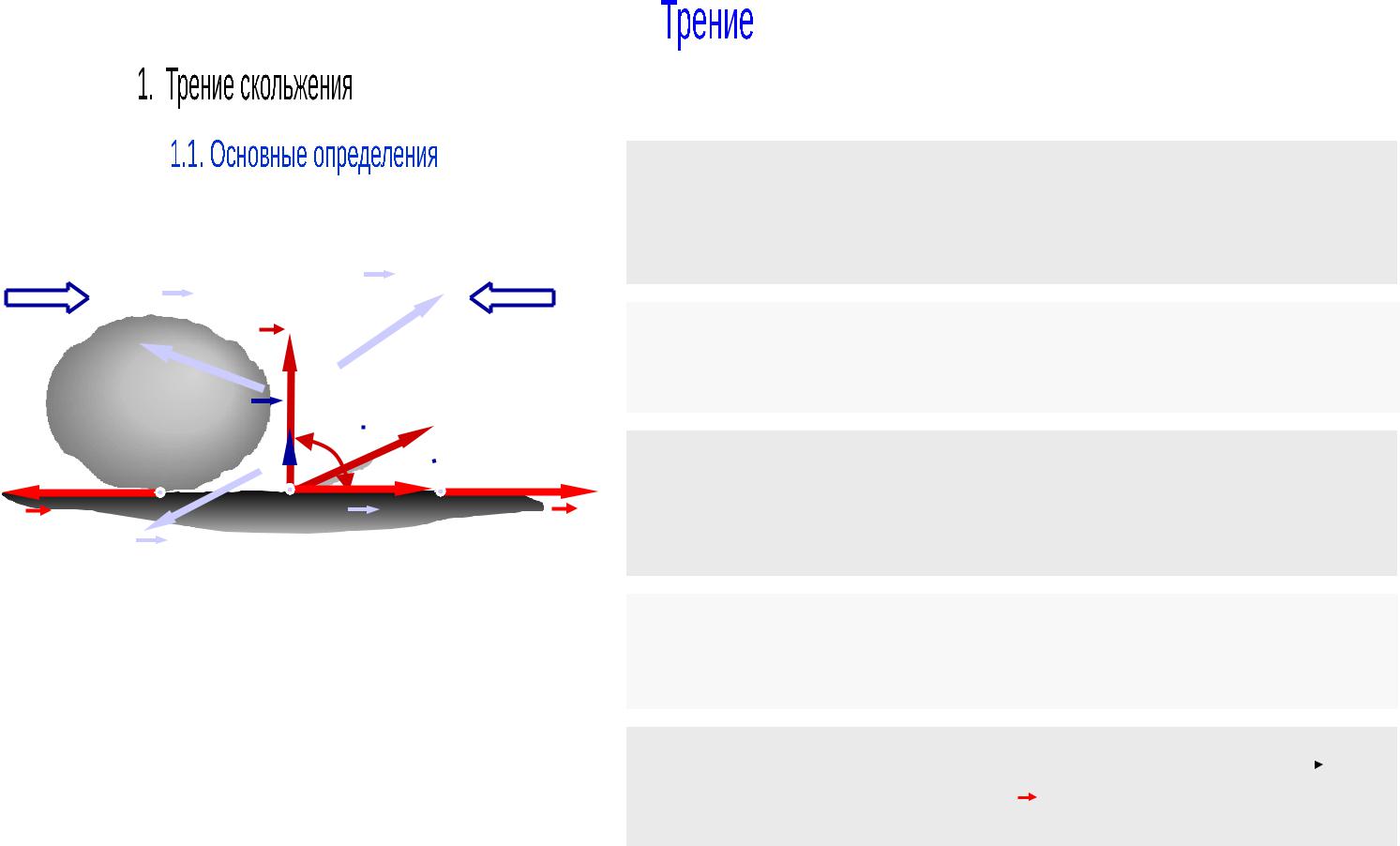
При движении или стремлении двигать одно тело по поверхности другого в касательной плоскости поверхностей возникает сила ТРЕНИЯ СКОЛЬЖЕНИЯ.
|
|
Fn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F1 |
|
|
|
Различают |
СИЛУ ТРЕНИЯ СКОЛЬЖЕНИЯ ПРИ |
||||||||||||||||
|
|
R |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
ПОКОЕ и |
СИЛУ ТРЕНИЯ СКОЛЬЖЕНИЯ В |
|||||||||||||||||||||||||||||||||||
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ДВИЖЕНИИ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
900 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При контакте абсолютно твердых и абсолютно |
||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
гладких поверхностей реакция в точке контакта |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
перпендикулярна к общей касательной плоскости тел |
|
|
Fтр |
F2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fтр |
|
|
|
Fтр и направление ее не зависит от внешних сил. |
|||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N ni 1 Fin ;
Fтр ni 1 Fi
При контакте деформируемых шероховатых тел реакция направлена под углом к общей касательной и ее направление зависит от внешних сил.
Разложив реакцию на касательную и нормальную
составляющие получим нормальную реакцию – N |
и |
силу трения скольжения – Fтр . |
|
F1
F2
R
Fn N 


















 Fтр
Fтр
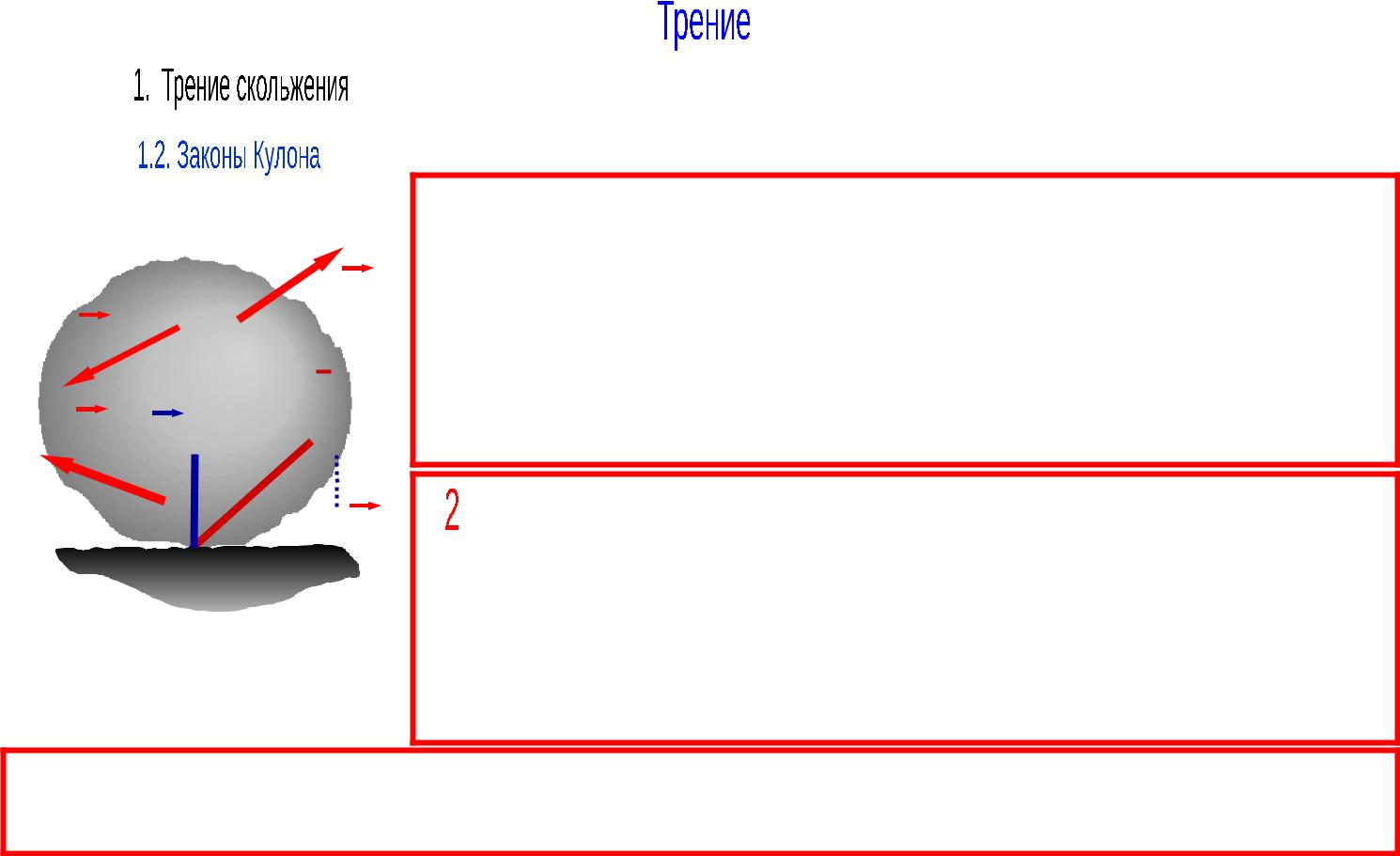
 Сила трения скольжения находится в общей касательной плоскости контактирующих тел и направлена в сторону, противоположную возможному движению. Величина силы зависит от активных сил и изменяется от нулевого до максимального значения, которое достигается при выходе тела из положения
Сила трения скольжения находится в общей касательной плоскости контактирующих тел и направлена в сторону, противоположную возможному движению. Величина силы зависит от активных сил и изменяется от нулевого до максимального значения, которое достигается при выходе тела из положения
равновесия: |
0 F |
F max |
|
||
|
тр |
тр |
Максимальная сила трения скольжения не зависит от площади соприкосновения тел и пропорциональна нормальному давлению
(реакции): |
F max f N |
|
|
|
тр |
f - коэффициент трения скольжения (безразмерен и не зависит от
площади соприкосновения тел).
 Коэффициент трения скольжения зависит от материала и физического состояния трущихся поверхностей (шероховатость, влажность, температура и др.)
Коэффициент трения скольжения зависит от материала и физического состояния трущихся поверхностей (шероховатость, влажность, температура и др.)
F1
F2
R
Fn Nφ














 Fтр
Fтр
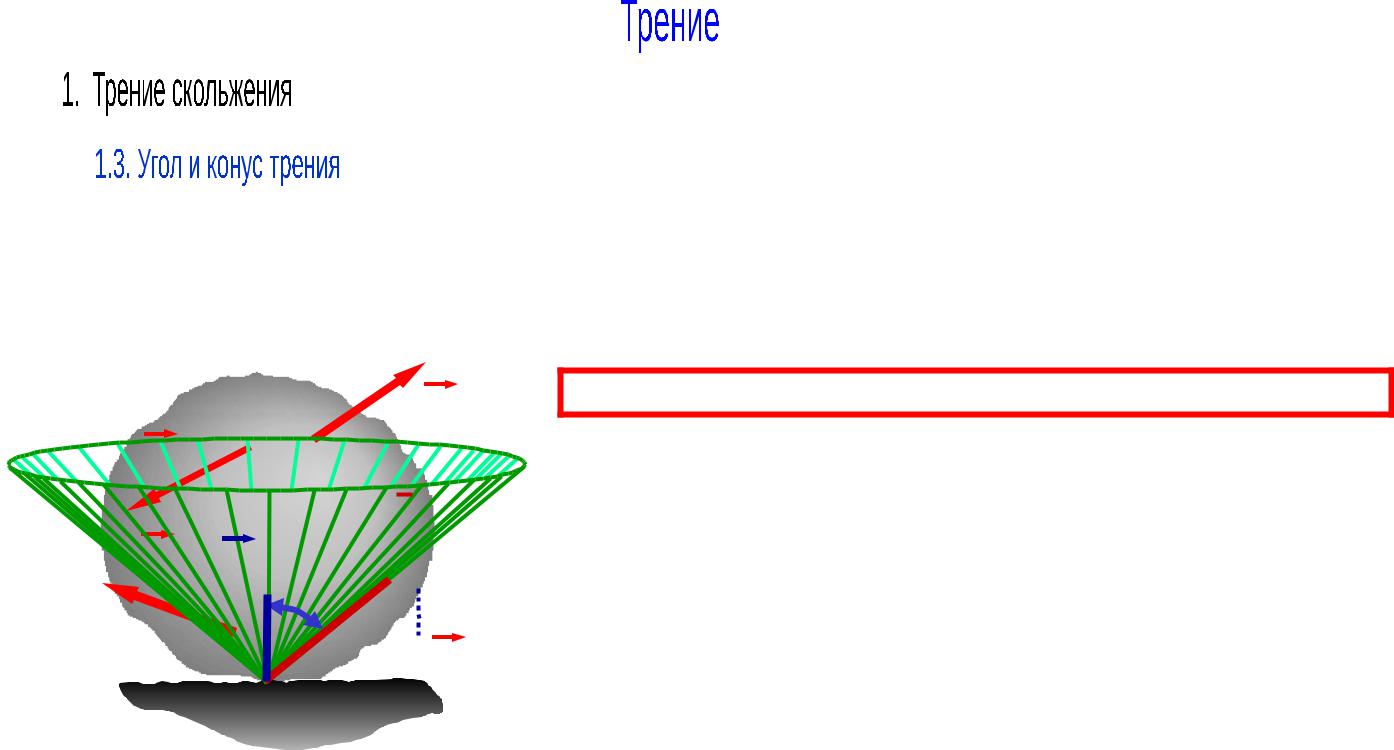
Угол между полной реакцией R и нормальной реакцией N при
максимальной силе трения Fтрmax называется углом трения. tg Fтрmax  N ; Fтрmax f N ; tg f
N ; Fтрmax f N ; tg f
ТАНГЕНС УГЛА ТРЕНИЯ РАВЕН КОЭФФИЦИЕНТУ ТРЕНИЯ
КОНУСОМ ТРЕНИЯ называется конус, описанный полной реакцией вокруг общей нормали соприкасающихся поверхностей при максимальной силе трения.
Конус трения может быть некруговым, если коэффициент трения разный в разных направлениях возможного движения (например из-за характера обработки поверхностей).
R
R 

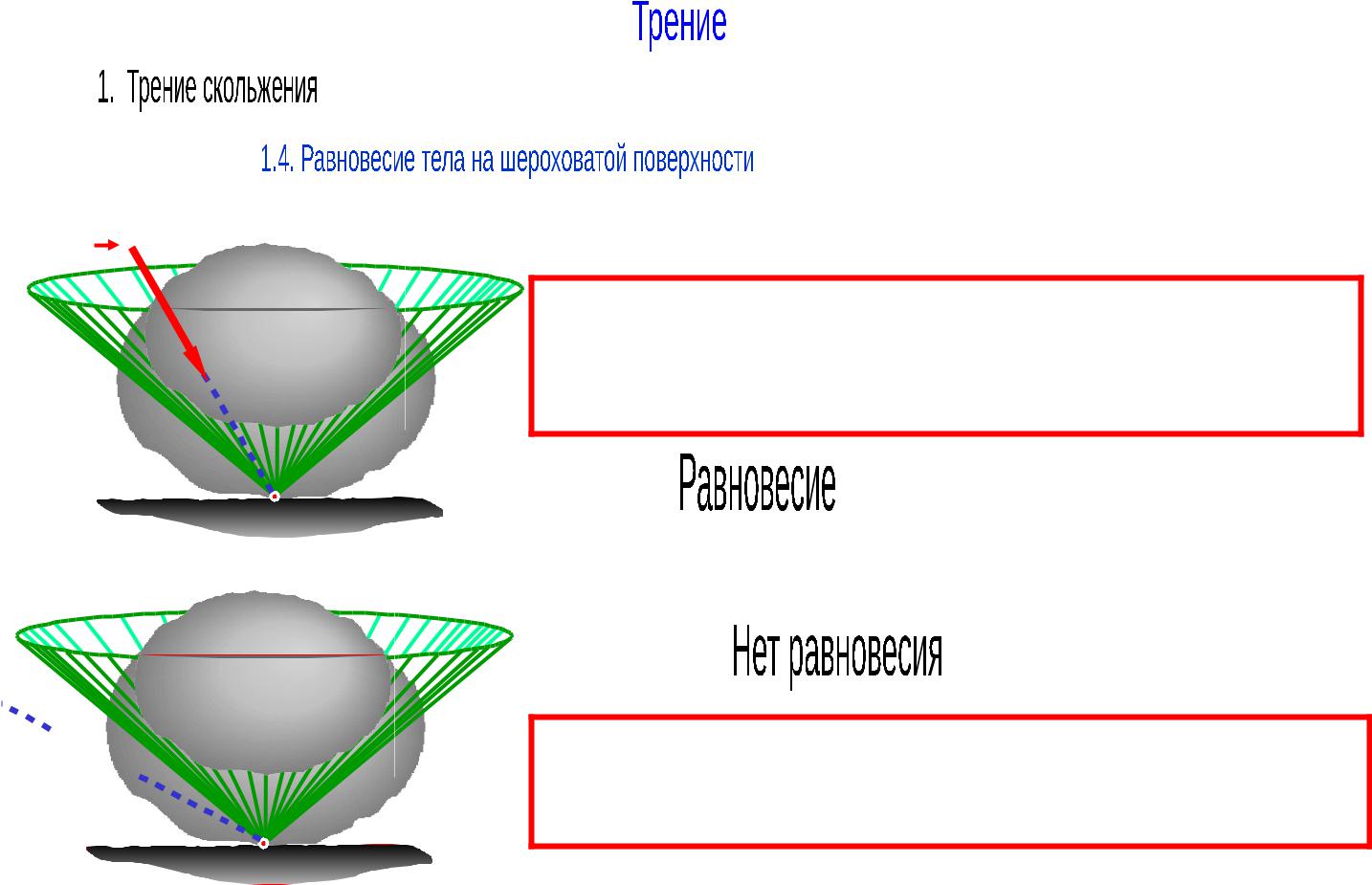
Если активные силы приводятся к равнодействующей, то тело находится в равновесии, если линия ее действия находится внутри или на образующей конуса трения.
Тело нельзя вывести из равновесия любой по величине активной силой, если ее линия действия проходит внутри конуса трения
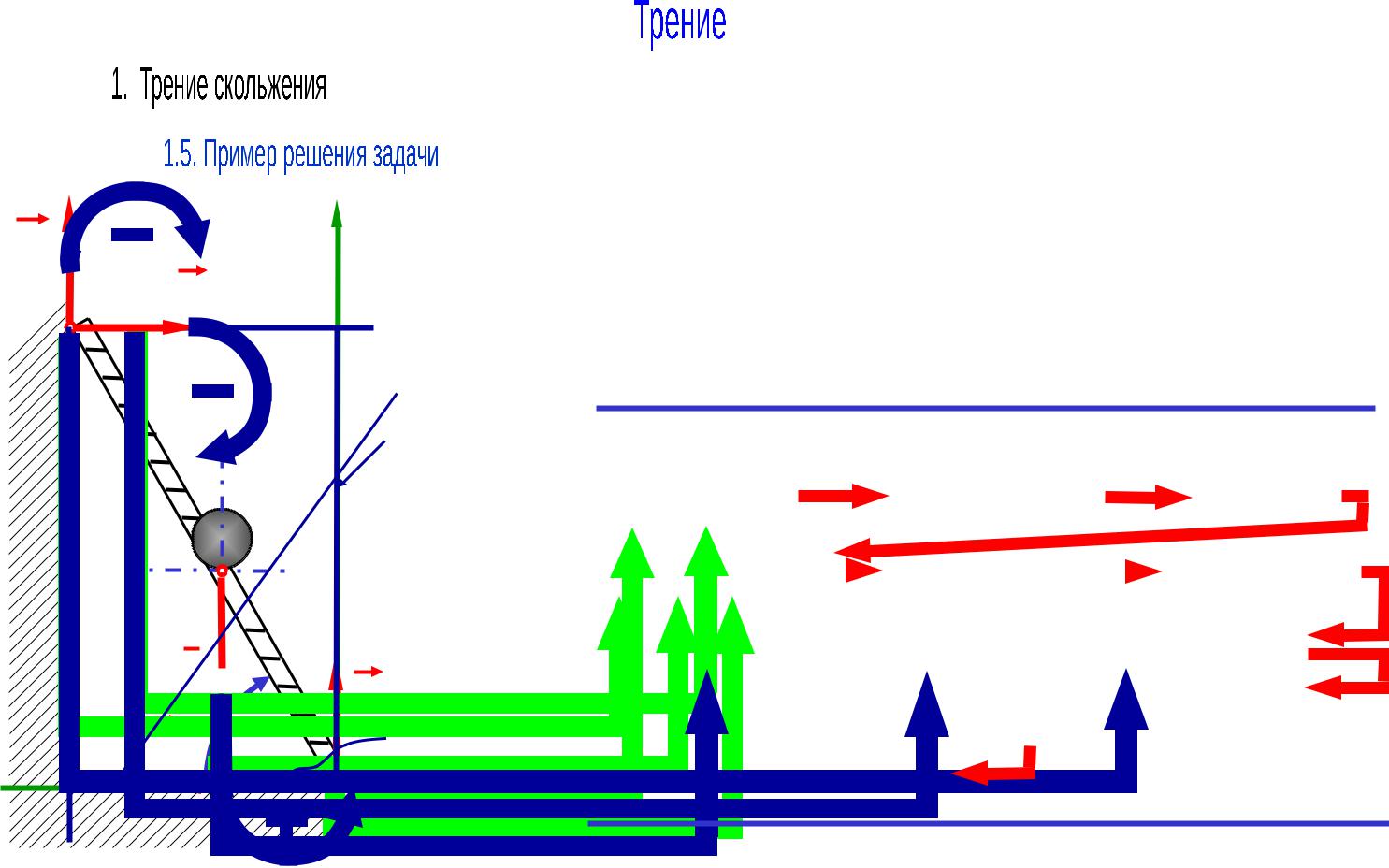
FA
тр A N1
P
C 
P

FB |
60 0 |
Лестница АВ опирается на негладкую стену и негладкий пол, y составляя с последним угол 600. Коэффициент трения лестницы о стену f1=0.2, лестницы об пол – f1=0.1. На лестнице размещается
|
|
|
груз P=2 кН. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Пренебрегая весом лестницы, определить расстояние ВС, при |
|||||||||||||||||||||||
h=AB cos600 |
|
котором лестница находится в равновесии, а также реакции пола |
||||||||||||||||||||||||
|
и стены. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
h=AB sin600 |
|
Решение: |
|
F A f |
1 |
N |
1 |
, F B |
|
f |
2 |
N |
2 |
. |
|
|
||||||||||
n |
|
|
|
|
|
|
тр |
|
|
|
тр |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Fxi 0; FтрB N1 |
0; |
|
|
f2 N2 N1 0; |
|
|
|
N1 f2 N2 ; |
||||||||||||||||||
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fyi 0; FтрA P N2 0; |
|
|
|
|
N2 P f1 f2 N2 0; |
|
N2 P /(1 f1 f2 ); |
|||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
N1 AB sin600 FтрA AB cos600 0; |
|||||||||||||||||
MB ( Fi ) 0; P BC cos600 |
||||||||||||||||||||||||||
i 1 |
|
|
|
0 |
|
f2 P |
|
|
|
|
|
0 |
|
f1 f2 P |
|
|
|
|
0 |
|
||||||
N h=BC cos600 |
P BC cos60 |
|
|
|
|
|
AB sin60 |
|
|
|
|
|
AB cos60 |
|
0; |
|||||||||||
|
1 f1 f2 |
|
1 f1 f2 |
|
|
|
||||||||||||||||||||
|
f2tg600 |
|
0.2 1.732 |
|
|
|
|
|
|
|
|
|
|
N2 P /( 1 f1 f2 |
) 1.96 кН ; |
|||||||||||
BC 1 f1 f2 |
AB 1 0.1 0.2 AB 0.34 AB; |
|
|
|
|
|||||||||||||||||||||
|
|
|
|
N1 f2 N2 0.196 кН |
||||||||||||||||||||||
|
|
|
Ответ: |
|
|
BC 0.34 AB; N1 |
0.196кН ; N2 1.96кН . |
|||||||||||||||||||
 Mтр
Mтр
L
O 
Q
 P
P
A
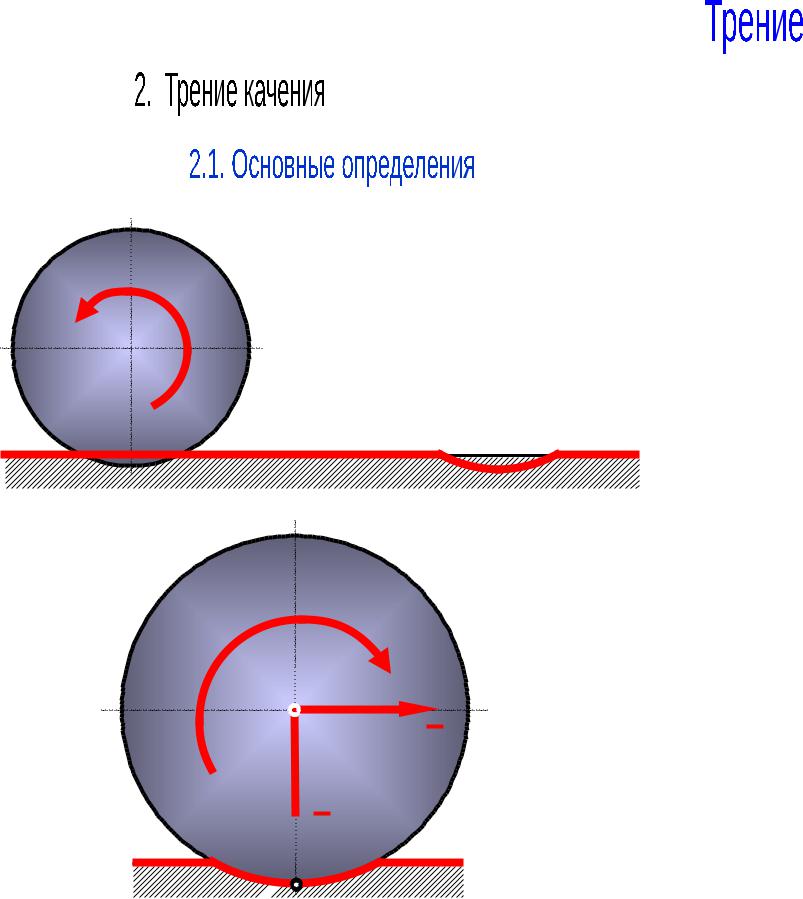
При качении одного тела по поверхности другого, вследствие деформаций поверхностей в зоне контакта, возникают силы, препятствующие качению. Это явление называется трением качения.
В месте контакта одновременно возможно возникновение и сил трения скольжения.
L 0, Q 0 ̶ведомо-ведущее колесо;
L 0, Q 0 ̶ведомое колесо;
L 0, Q 0 ̶ведущее колесо;
Чистое качение – точка соприкосновения катка не скользит по поверхности.
Качение со скольжением – точка касания скользит по поверхности.
Чистое скольжение – каток движется не имея вращения.
Fn |
F1 |
F2 R O 






































 N
N







 M
M
F |
A |
D |
|
||
O |
|
Q
 P
P
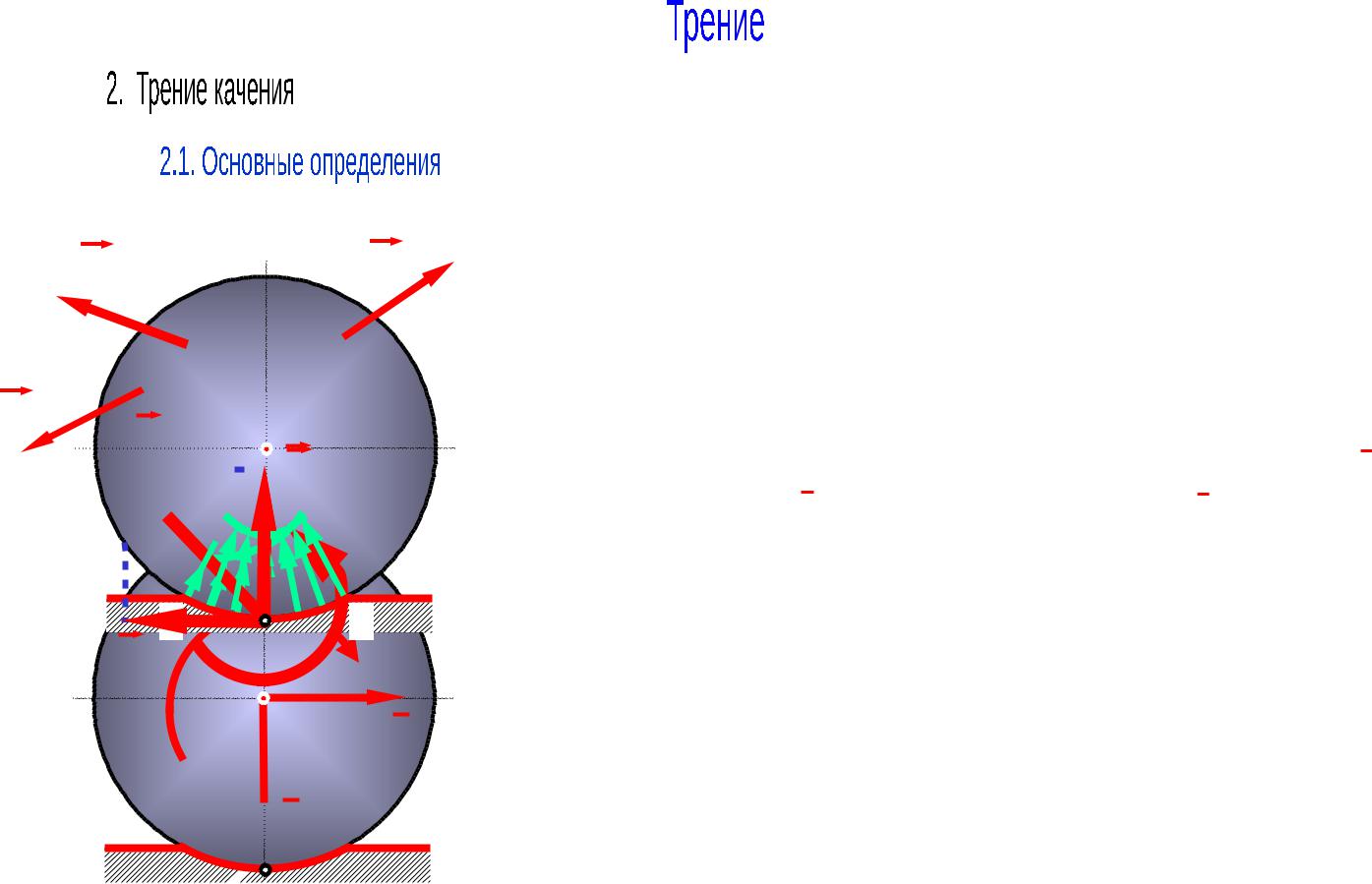
Вследствие деформации соприкасающихся поверхностей катка и поверхности качения зона контакта представляет некоторую линию BAD. По этой линии на колесо действуют распределенные силы реакции.
Распределенные силы реакции приводятся к точке А. При этом образуется главный вектор этих сил R с
с
составляющими N (нормальная реакция) , F
(нормальная реакция) , F (сила трения
(сила трения
скольжения) и главный момент сил реакции – M.
В случае симметричного расположения распределенных сил реакции по дуге BAD при приведении их к точке А, момент пары сил M и сила трения скольжения F будут равны нулю.
В этом случае нет активных сил, стремящихся катить тело в какую-либо сторону.
A
Fn |
F1 |
F2 |
O |
|
N M |
D
F A
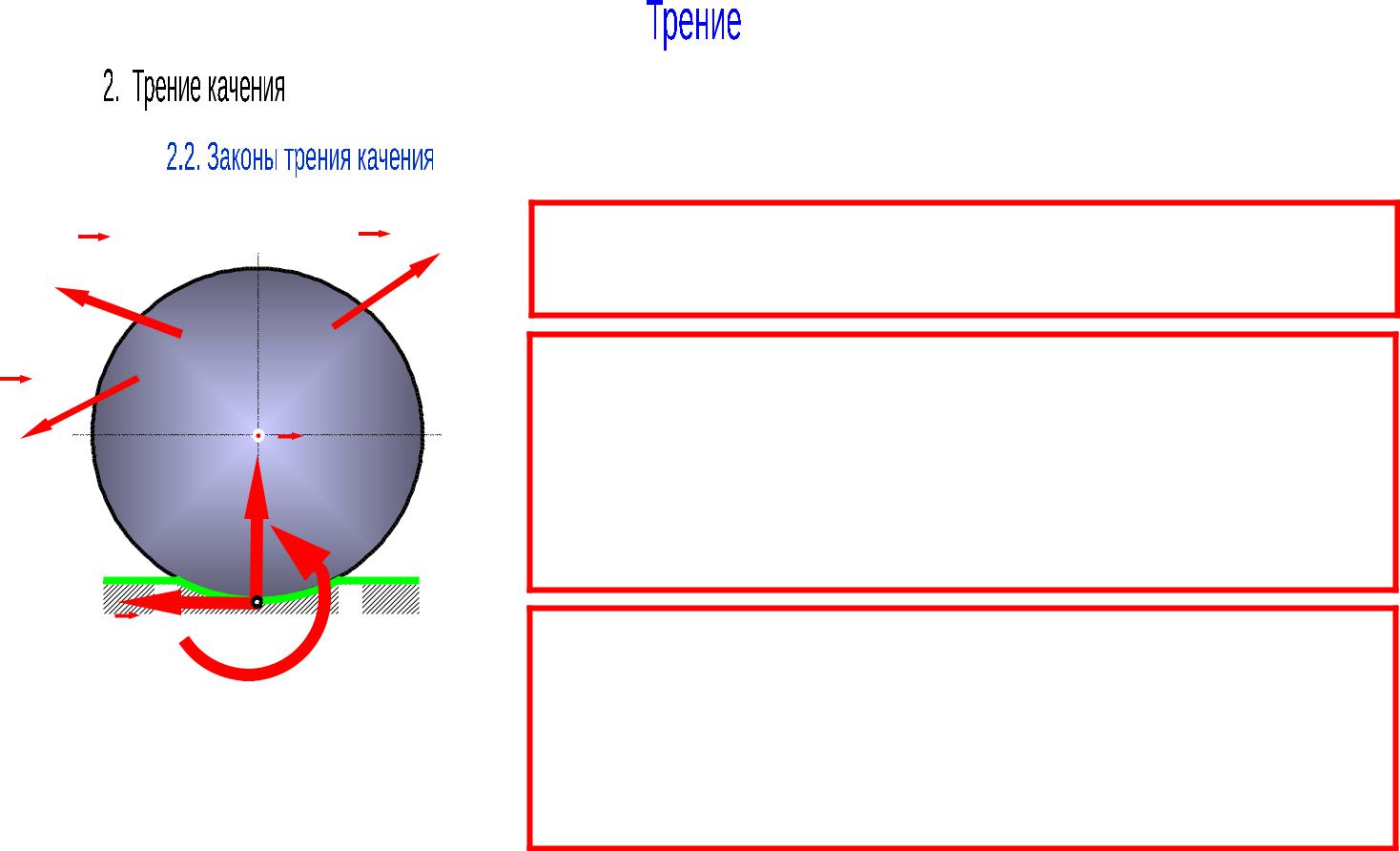
Законы справедливы для не очень больших нормальных давлений и не сильно деформируемых поверхностей контакта.
 Момент трения качения не зависит от радиуса катка.
Момент трения качения не зависит от радиуса катка.
 Максимальное значение момента трения качения пропорционально нормальному давлению (реакции): Mтрmax.кач N
Максимальное значение момента трения качения пропорционально нормальному давлению (реакции): Mтрmax.кач N
δ - коэффициент трения качения (безразмерен).
 Коэффициент трения качения зависит от материала и состояния контактирующих поверхностей и в первом приближении не зависит от угловой скорости качения и скорости скольжения.
Коэффициент трения качения зависит от материала и состояния контактирующих поверхностей и в первом приближении не зависит от угловой скорости качения и скорости скольжения.
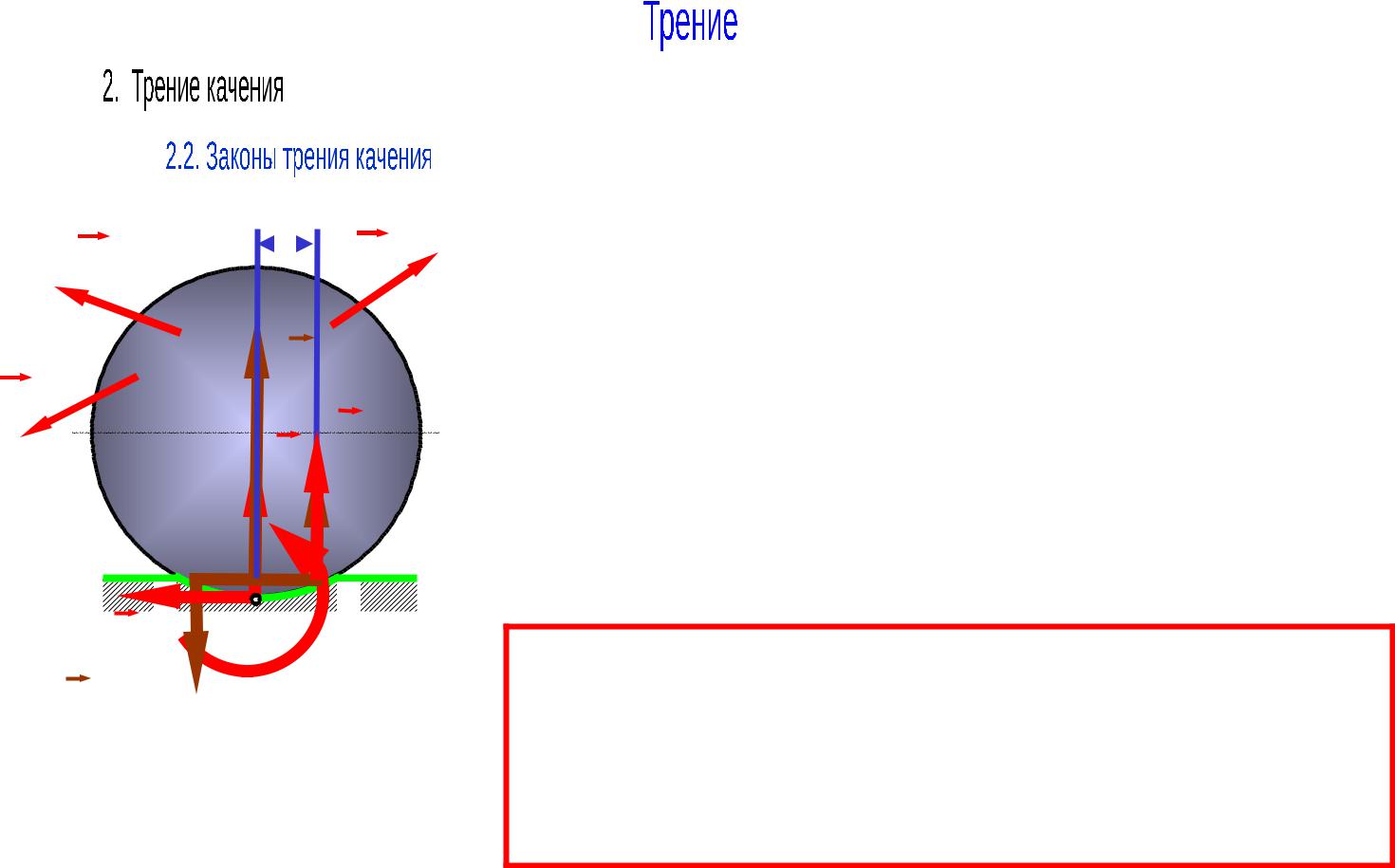
d
Fn 
 F1
F1
F2 |
N' |
|
O |
N |
|
|
N |
|
|
|
M |
F |
A |
D |
|
||
|
|
|
N'' |
|
|
Законы позволяют рассматривать трение качения для абсолютно твердых тел, соприкасающиеся в одной точке.
N , N N ;
N N N ;
d Mmax N .
N N
В предельном случае равновесия, пара сил трения качения может быть заменена смещением нормальной реакции относительно точки касания в сторону вращения на величину δ. В этом случае момент, образуемый нормальной реакцией относительно точки А будет равен моменту трения качения.
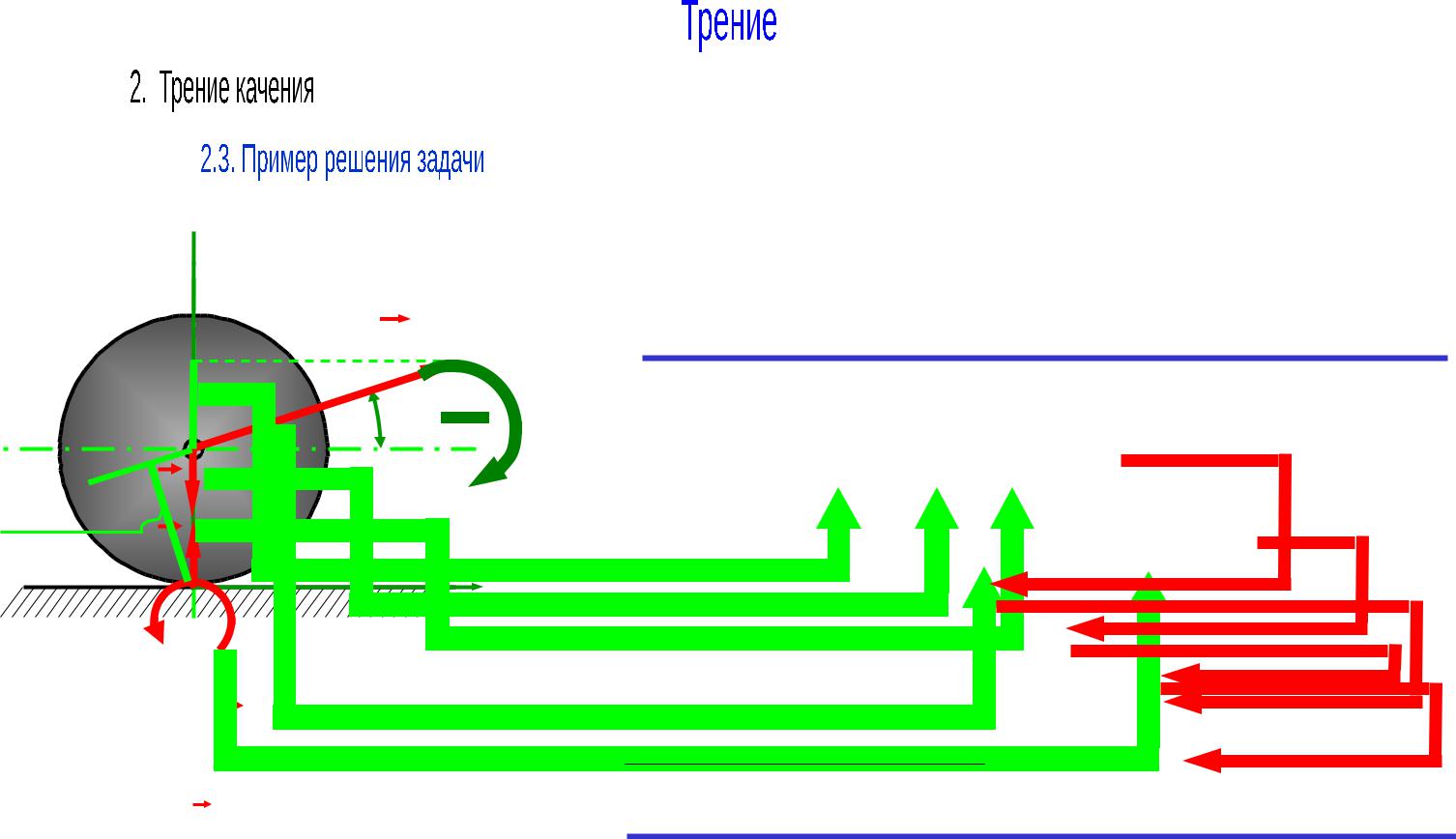
y 
P
Определить силу P, необходимую для равномерного качения цилиндрического катка диаметра d=60cм и веса G=300Н по горизонтальной плоскости, если коэффициент трения качения k=0.5cм, а угол, составляемый силой с горизонтом, равен α=300.
Py = Psinα |
α |
|
Решение: |
M k N |
|
|
in 1 Fyi 0; |
P sin G N 0; |
|||
G |
|
||||
h=0.5d cosα |
|
in 1 |
MO ( Fi ) 0; P 0.5d cos M 0; |
||
N |
|
||||
O |
|
|
N G P sin ; |
||
M |
|
P 0.5d cos k N 0; |
|||
Силы, действующие на каток: |
P 0.5d cos k(G P sin ) 0; |
||||
Активные: – – |
|
|
|
k G |
|
– |
|
P 0.5d cos k sin 5.72H ; |
|||
Реакции: – N – реакция поверхности; |
Ответ: |
|
P 5.72H . |
||
– М – момент трения качения. |
|
||||
