
- •Алгебраический момент силы (относительно точки) – алгебраическая величина, равная произведению модуля силы на
- •Векторный момент силы (относительно центра) - векторная величина, равная векторному произведению радиус-вектора на
- •Модуль векторного момента силы относительно точки О определяется как удвоенная площадь треугольника ОАВ:
- •1.2.1. Силы различны по модулю
- •1.2.2. Силы равны по модулю
- •1.2.2. Силы равны по модулю
- •2.1.1. Определение
- •2.1.2. Знак момента
- •2.1.3. Геометрическая интерпретация
- •2.2.1. Определение
- •2.2.2. Модуль векторного момента
- •2.2.3. Геометрическая интерпретация
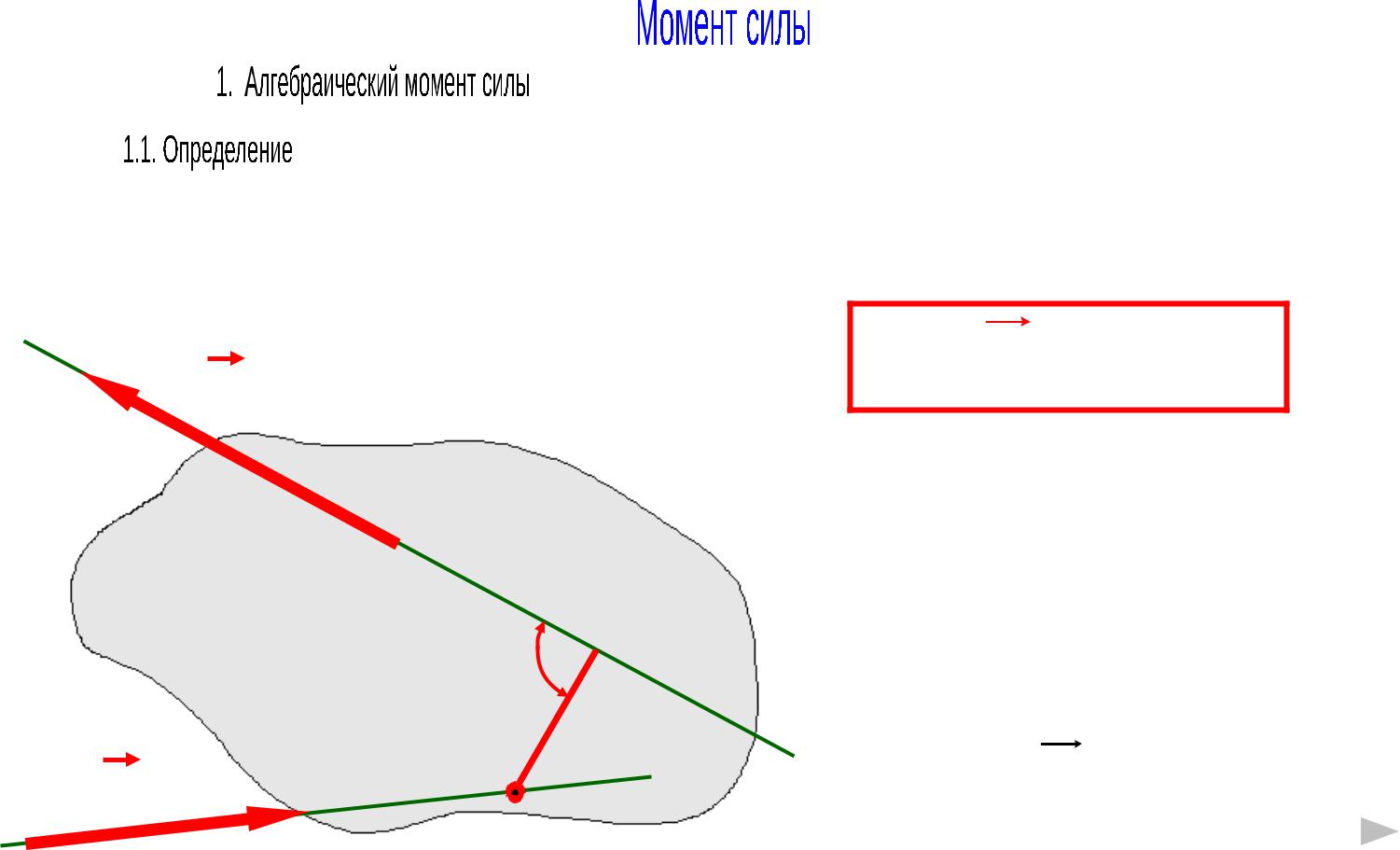
Алгебраический момент силы (относительно точки) – алгебраическая величина, равная произведению модуля силы на плечо силы
B |
F |
|
MO ( F ) F h |
|
|
|||
|
|
Плечо |
силы |
– кратчайшее |
||||
|
A |
|
||||||
|
|
расстояние |
от |
точки |
до |
|||
|
|
|
линии |
действия |
силы |
|||
|
|
900 |
(величина |
перпендикуляра, |
||||
|
|
проведенного |
из |
точки |
к |
|||
|
|
h |
линии действия силы) |
|
|
|||
P |
O |
|
MO ( P ) 0 |
|
|
|||
|
|
|
|
|||||
|
|
|
Щелчок для |
|||||
продолжения
|
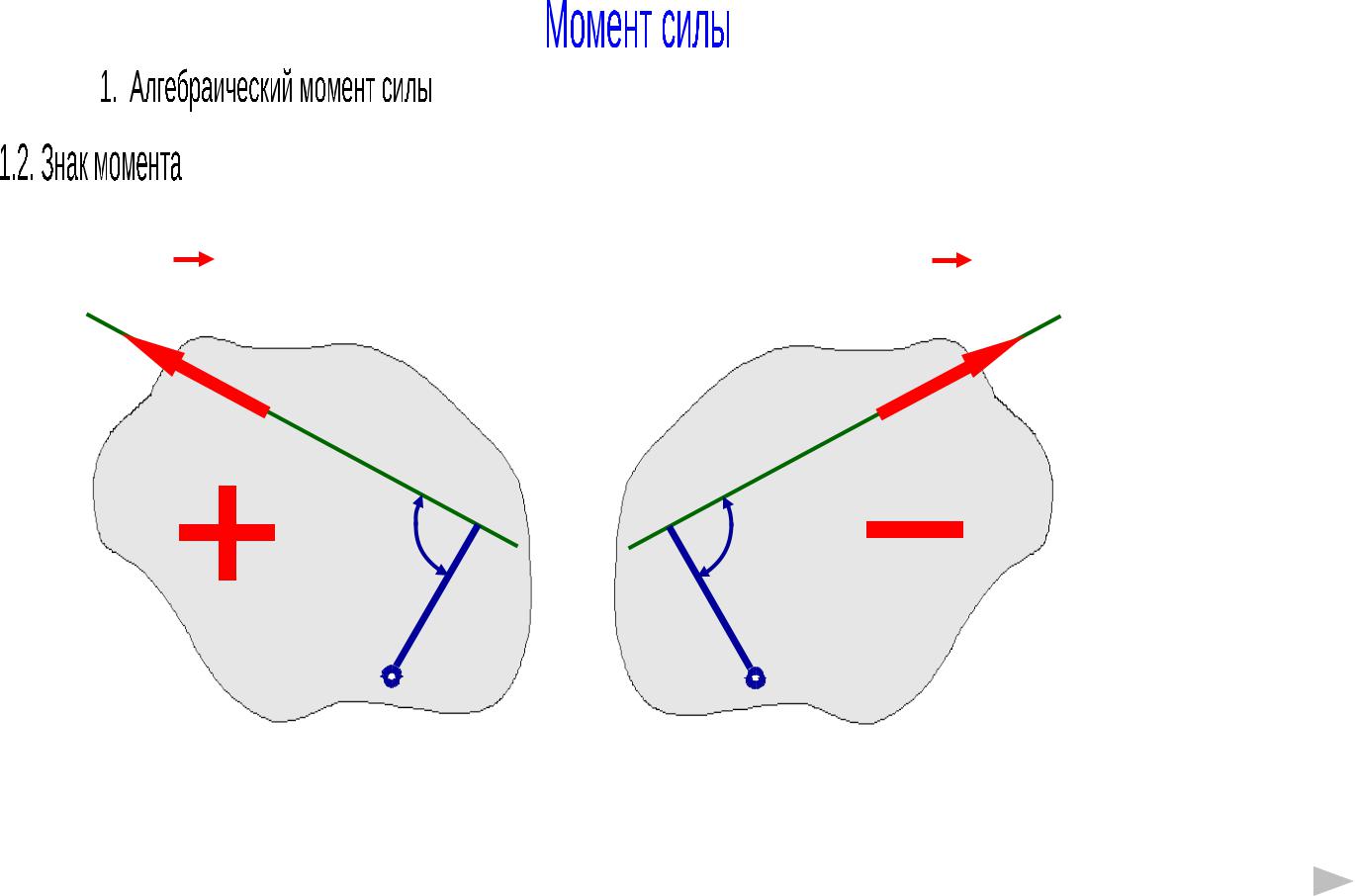
Знак момента определяется направлением |
|
возможного вращения тела вокруг точки |
F |
под действием силы. F |
900 |
900 |
h |
h |
O |
O |
Вращение против часовой |
Вращение по часовой стрелке |
стрелки – знак плюс (+) |
– знак минус (-) |
Щелчок для продолжения
B
900
h
O
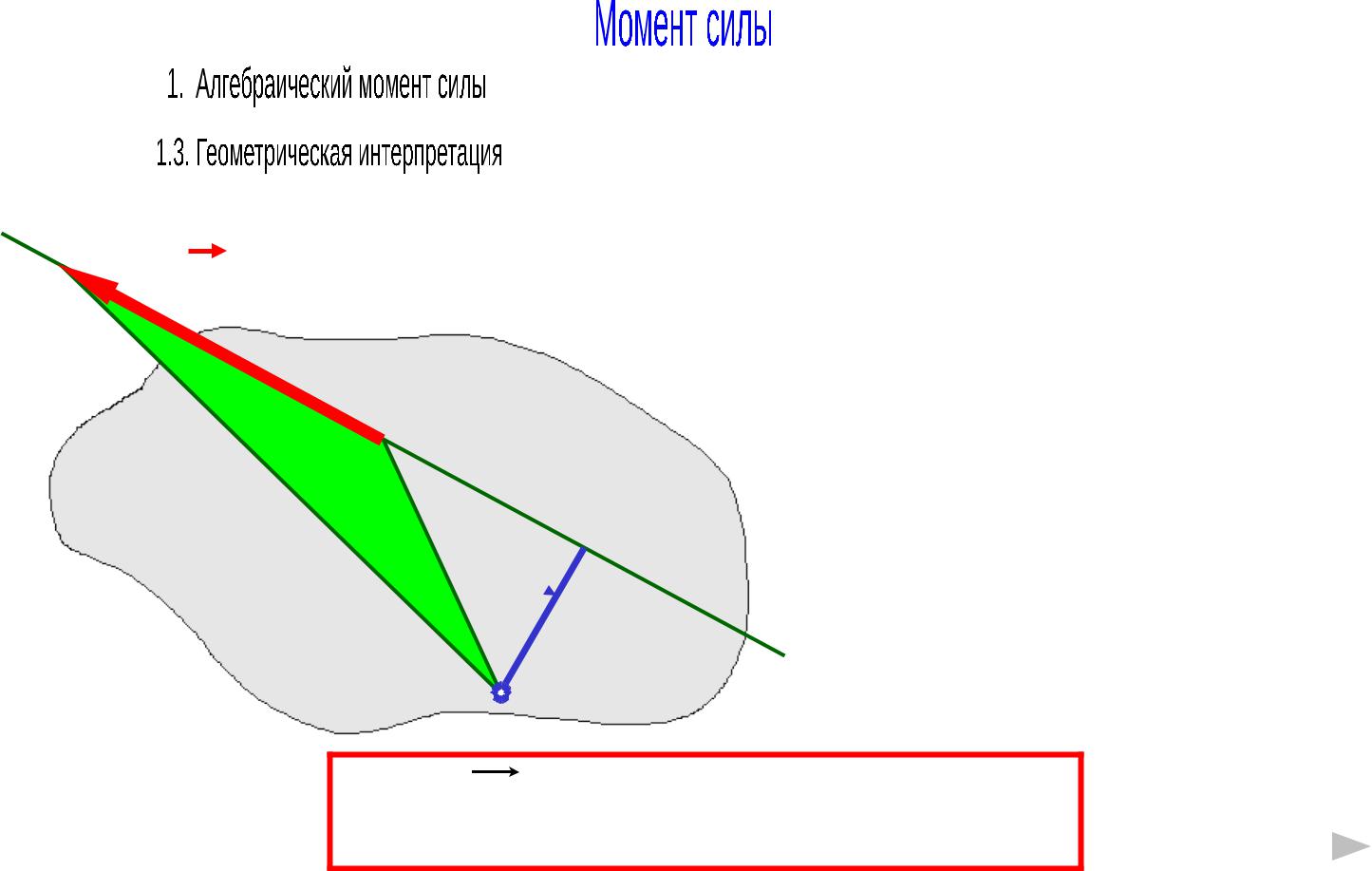
Алгебраический момент силы относительно точки численно равен удвоенной площади треугольника, построенного на отрезке AB и моментной точке О
MO ( F ) F h 2 SOAB
Щелчок для продолжения
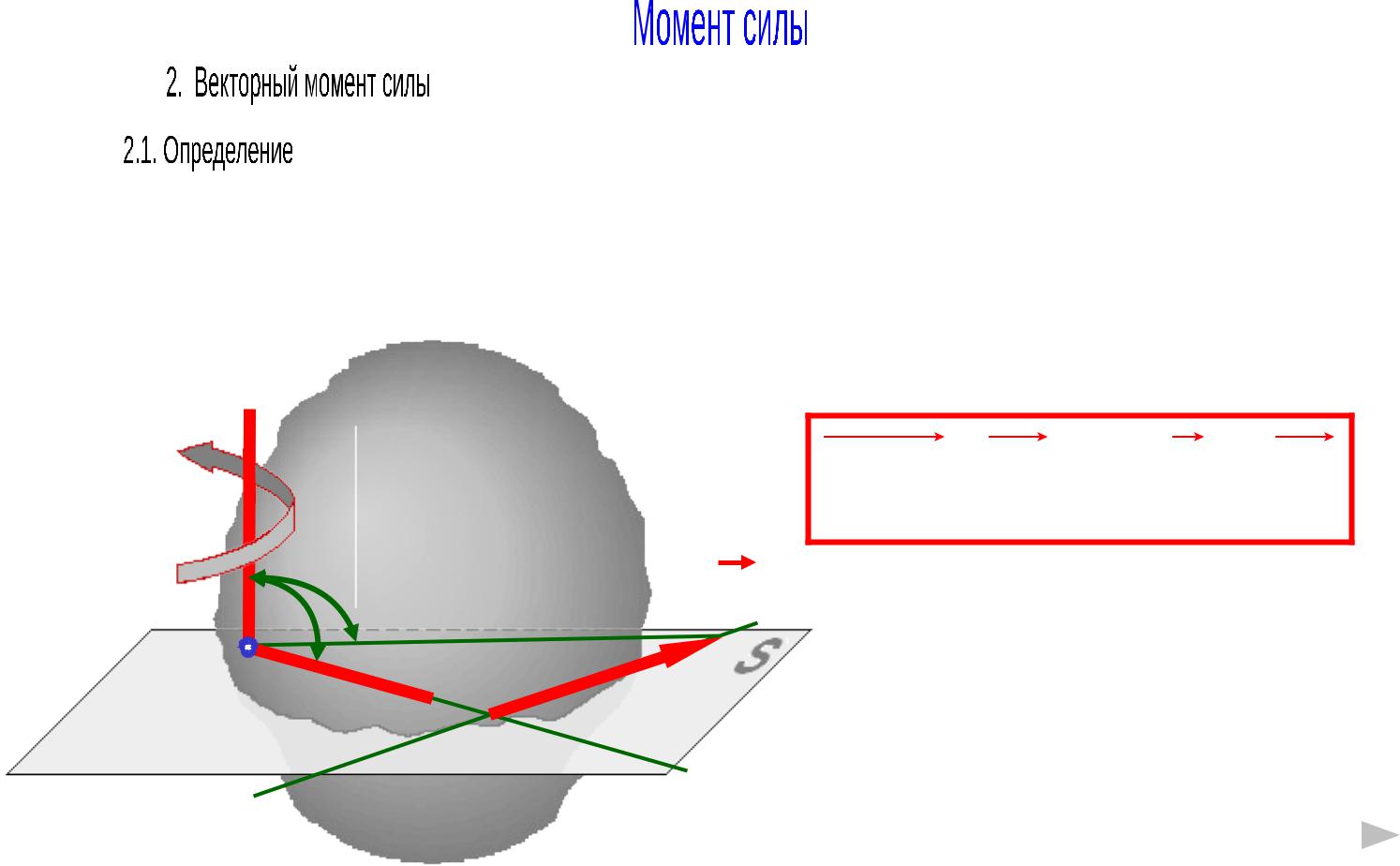
Векторный момент силы (относительно центра) - векторная величина, равная векторному произведению радиус-вектора на вектор силы:
 M
M

MO ( F ) r F
900 |
F |
O |
|
r 

Щелчок для продолжения
 M
M

O |
|
900 |
90h0 r |
A |
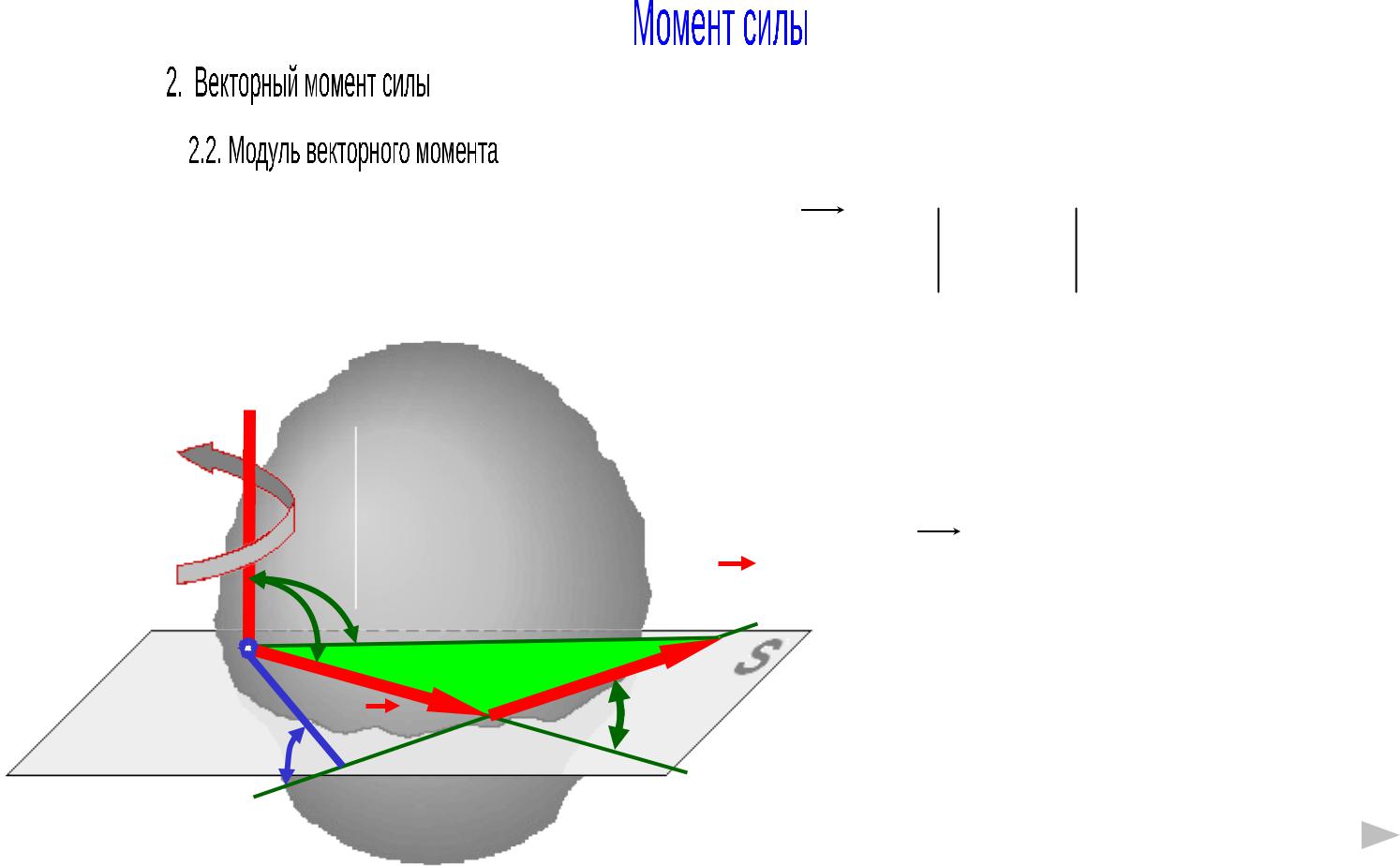
MO ( F ) r F r F sin
Модуль векторного момента численно равен удвоенной площади треугольника ОАВ:
h r sin
F |
MO ( F ) h F 2 SOAB |
||||
|
|
|
|
|
|
B |
|
|
Модуль векторного момента |
|
|
|
|
равен |
алгебраическому |
|
|
α |
|
|
моменту |
|
|
|
|
|
|
|
|
Щелчок для продолжения
z 
Z |
Fz |
F |
X |
|
|
|
|
A |
k |
j |
z Fy YZ |
i O |
|
x |
Fx |
y |
|
x |
XY |
|
|
|
|
i |
j |
k |
MO ( F ) |
x |
y |
z |
|
Fx |
Fy |
Fz |
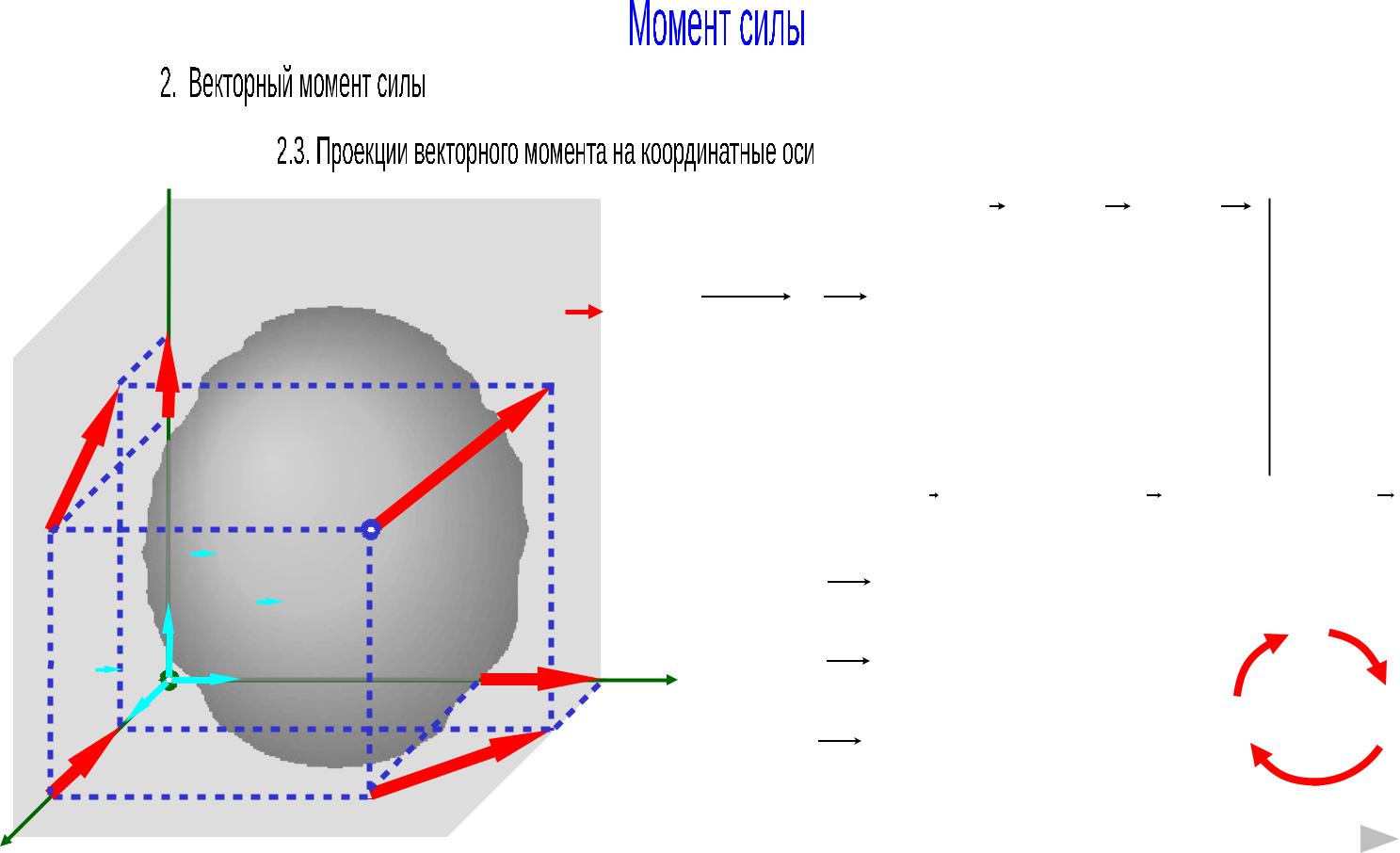
MO ( F ) ( yFz zFy )i ( zFx xFz )j ( xFy yFx )k
Mx ( F ) yFz zFy |
x |
y M y ( F ) zFx xFzz |
y |
Mz ( F ) xFy yFx |
|
|
Щелчок для |
|
продолжения |
F
z 
O |
h FS |
900 |
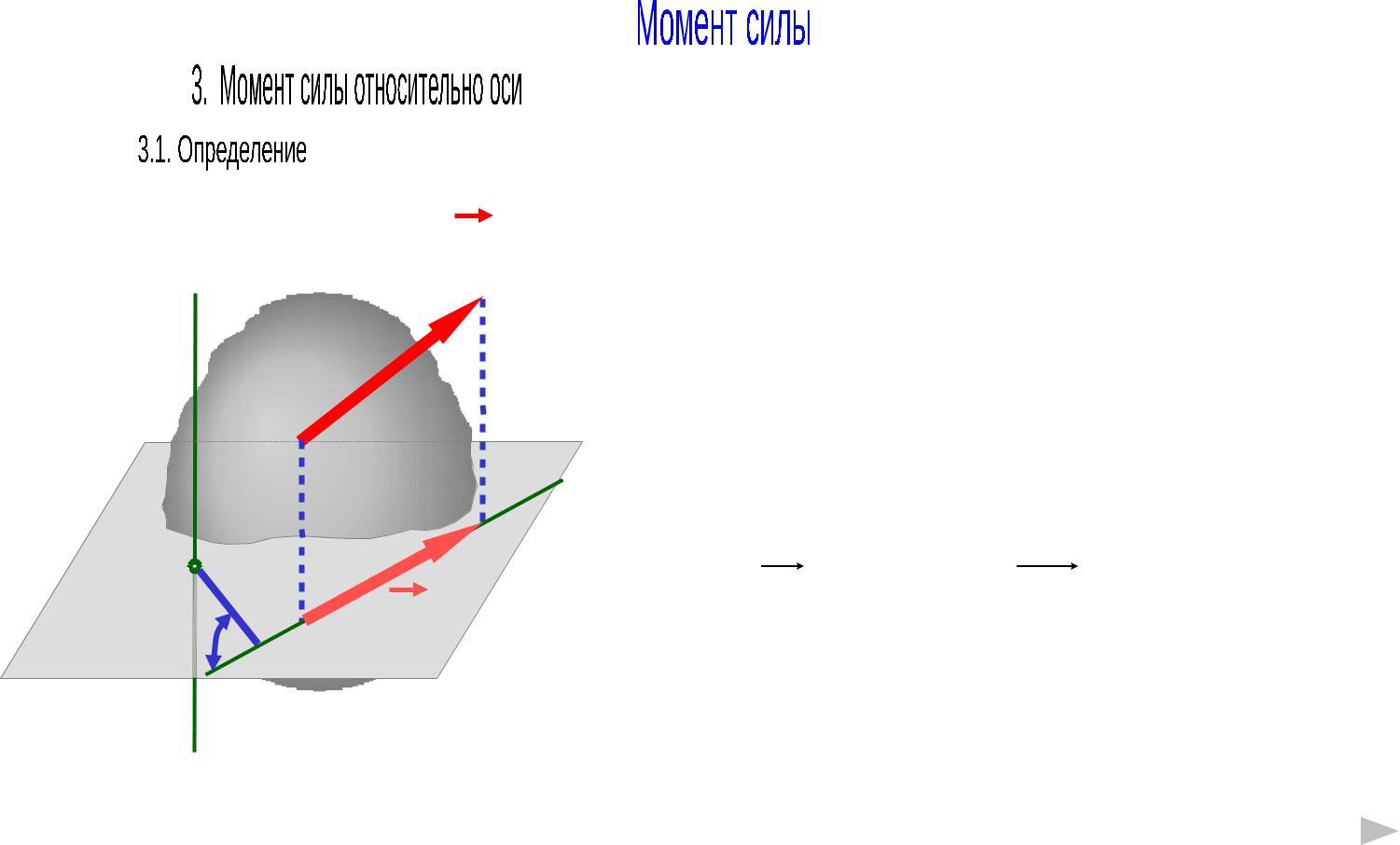
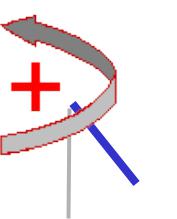
Момент силы относительно оси определяется как алгебраический момент проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.
Mz ( F ) MO ( FS ) h FS
Щелчок для продолжения
F
z 
 FS
FS
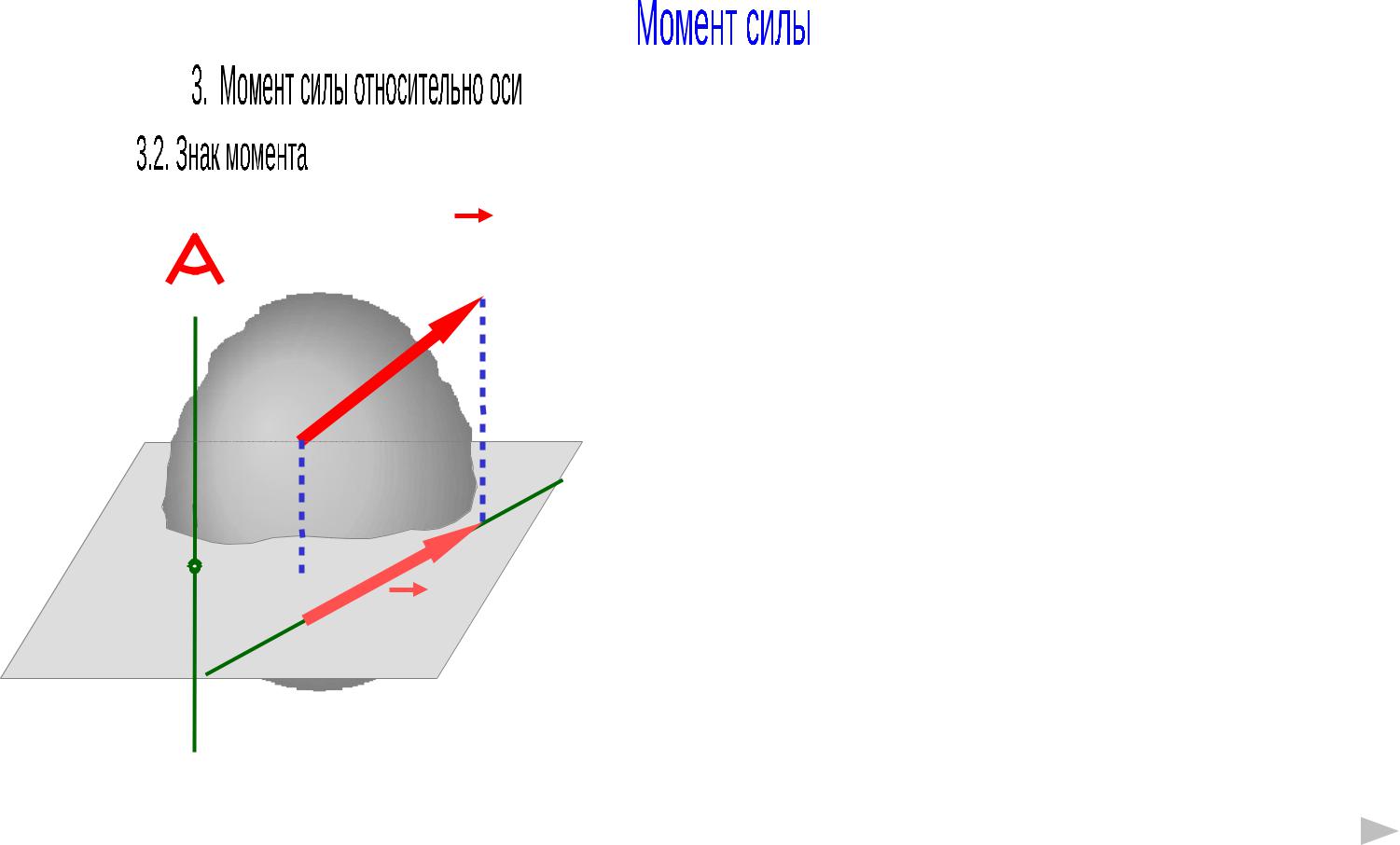
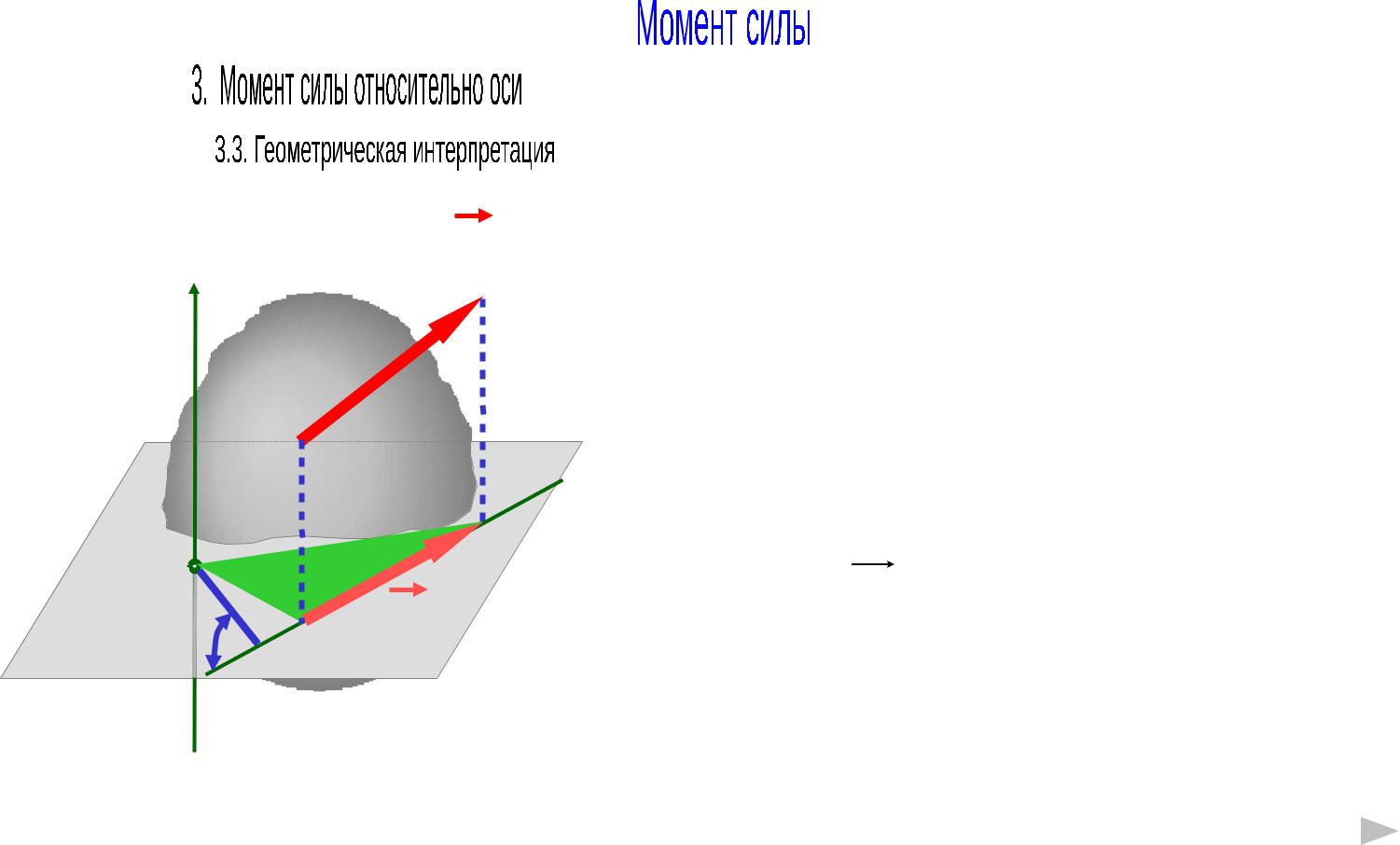
Момент силы относительно оси считается положительным (+), если при наблюдении из конца оси,
проекция силы FS |
на плоскость |
|
стремиться вращать тело против |
||
часовой стрелки. |
|
|
Момент |
силы относительно оси |
|
считается отрицательным (-) |
||
при |
стремлении |
вращения |
по часовой стрелке. |
|
|
Щелчок для продолжения
z |
|
FB |
|
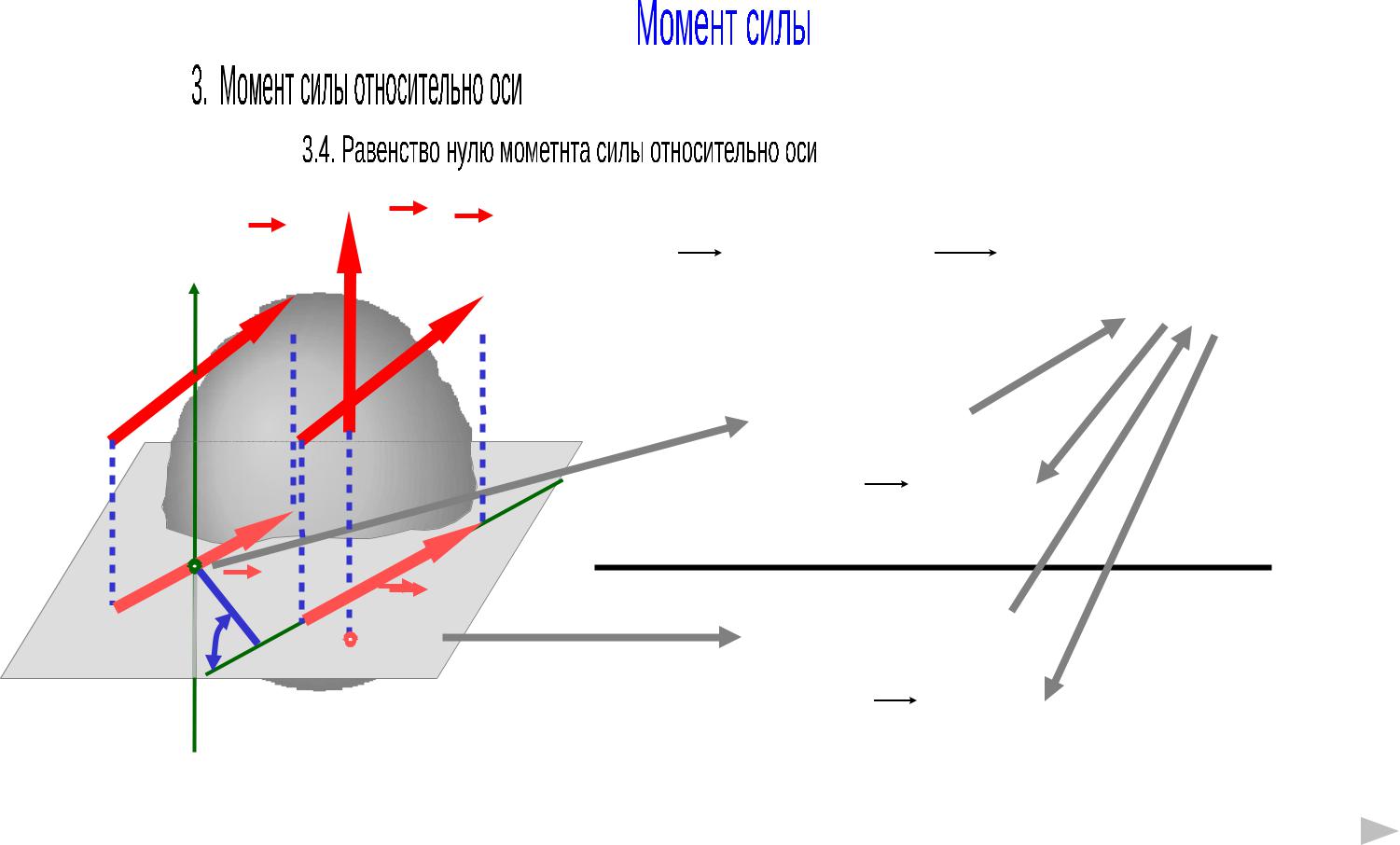
Момент |
силы относительно оси |
|
|
|
|
|
|||
|
|
|
|
можно |
выразить как |
удвоенную |
|
A |
|
|
площадь |
треугольника |
ОА1В1, |
|
|
|
построенного на проекции силы FS и |
|||
|
|
|
|
|||
O |
|
|
B1 |
точке О пересечения оси с плоскостью. |
||
|
|
Mz ( F ) 2 SOA1B1 |
||||
h |
A1 |
S |
|
|||
900 |
|
|
|
|
||
Щелчок для продолжения
z F |
|
F F |
|
M |
( F ) M |
( F ) h F |
|
|
|
|
|||||
|
|
|
|||||
|
|
|
|
z |
O |
S |
S |
|
|
|
|
||||
h 0
O |
|
Mz ( F ) 0 |
Fh0 S |
FSS |
F 0 |
90 |
|
S |
Mz ( F ) 0
Щелчок для продолжения
z 
α |
Mz |
MO |
A |
O |
A1
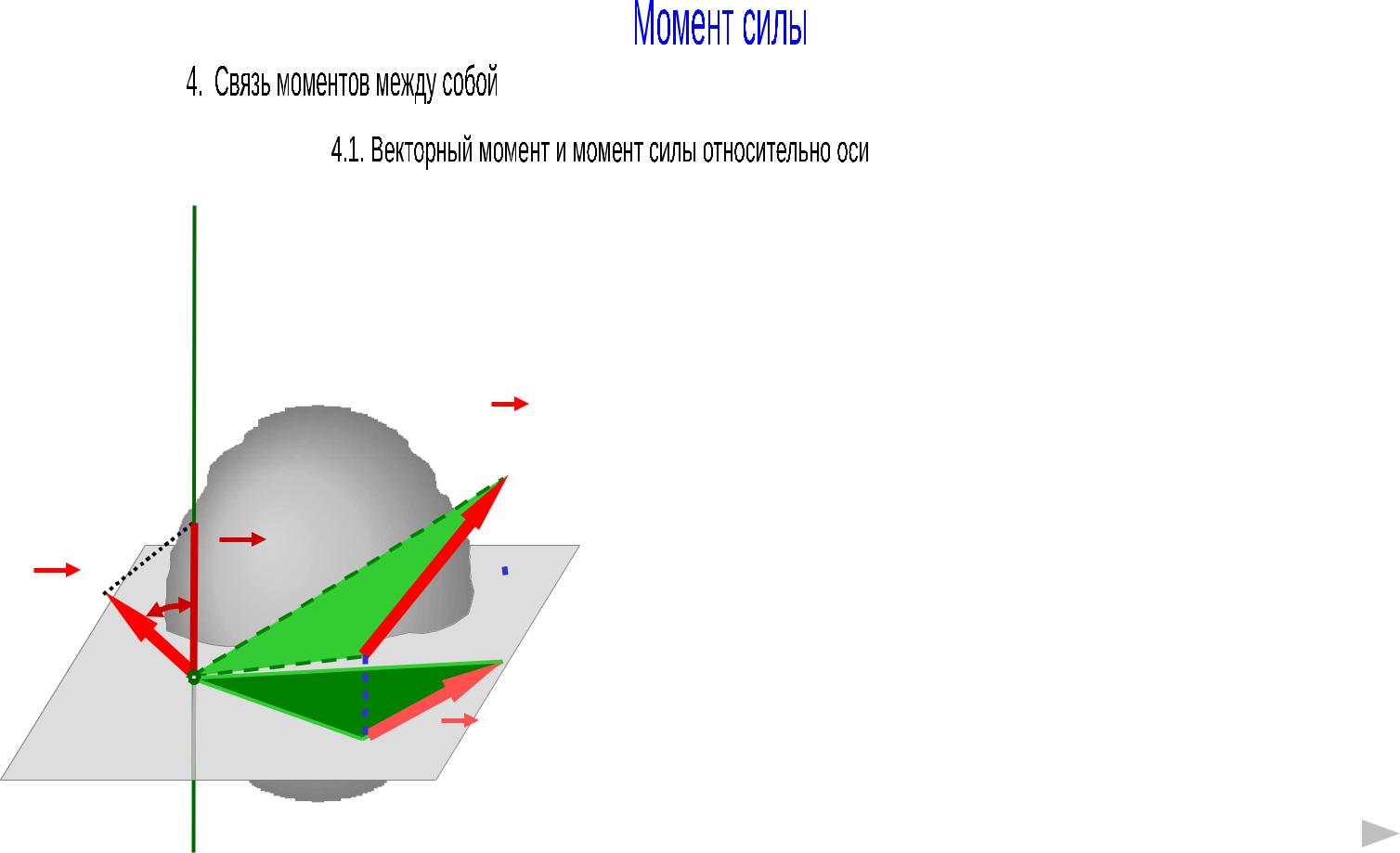
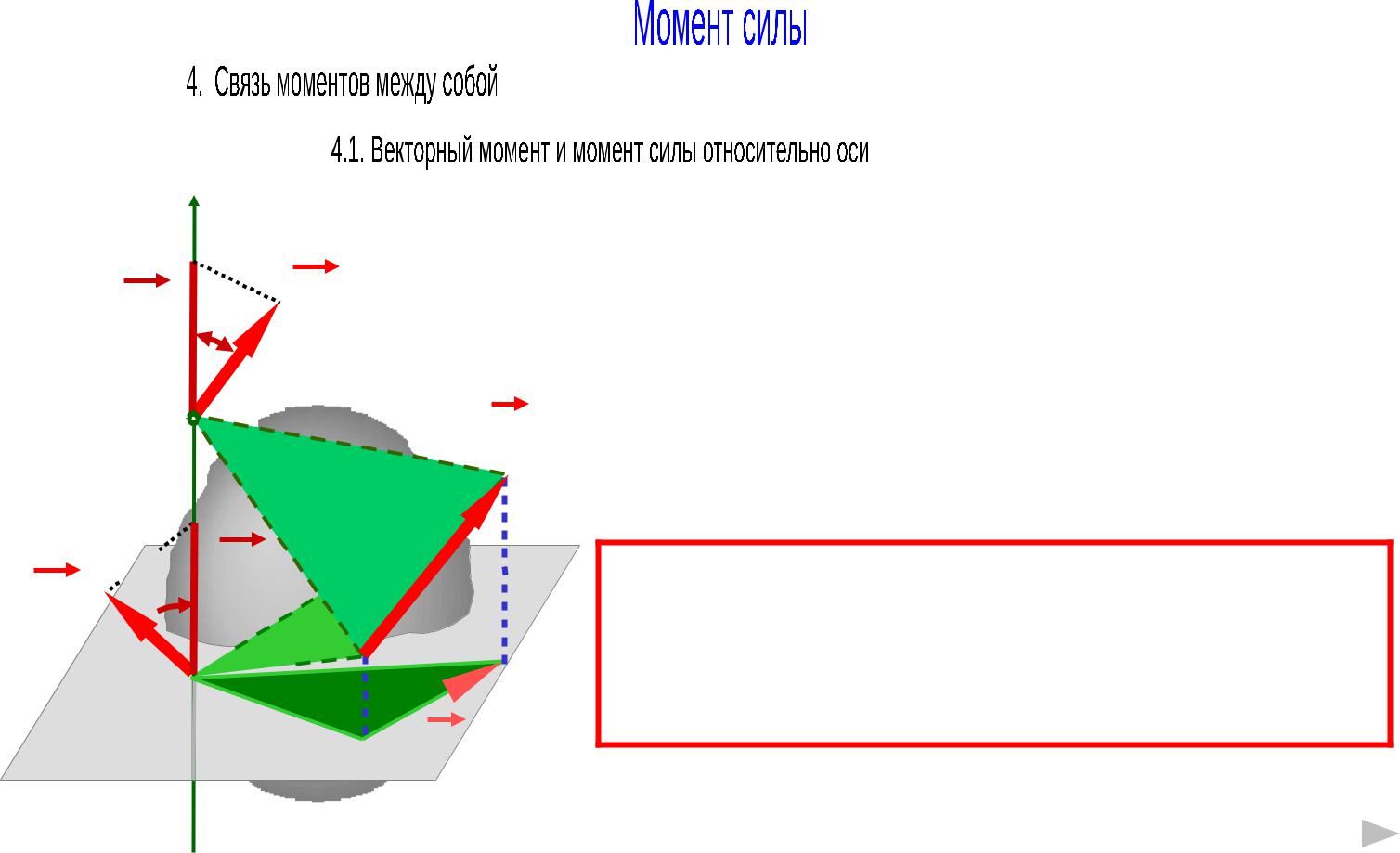
Модуль векторного момента силы относительно точки О определяется как удвоенная площадь треугольника ОАВ:
|
|
|
|
MO ( F ) 2 SOAB |
|
|
|||
|
|
|
|
Момент силы относительно оси, проходящей |
|||||
|
|
|
|
через точку О, определяется как удвоенная |
|||||
F |
|
|
|
площадь треугольника ОА1 В1 : |
|
|
|||
|
|
|
Mz |
( F ) 2 SOA B |
1 |
|
|||
|
|
||||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
На основании теоремы о проекции плоской |
|||||
|
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
фигуры (площадь проекции плоской фигуры |
|||||
|
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
равна площади самой фигуры, умноженной на |
|||||
|
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
||||||
|
|
|
|
||||||
|
|
|
B1 |
косинус угла |
|
|
между плоскостями фигуры и |
||
|
|
|
|
|
|||||
|
|
|
|
|
|||||
|
|
|
|
|
|||||
|
|
|
проекции): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
FS |
SOA B |
|
SOAB cos( ) |
|
|
||||
1 |
1 |
|
|
|
|||||
|
|
|
|
|
|
|
|||
|
|
|
|
Mz ( F ) MO ( F ) cos( ) MOz ( F ) |
Щелчок для |
||||
|
|
|
|
|
|
|
|
|
продолжения |
|
z |
|
Модуль векторного момента силы относительно точки О1 |
||||
|
|
определяется как удвоенная площадь треугольника О1АВ: |
|||||
|
|
|
|||||
Mz |
α1 M |
O1 |
|
MO1 ( F ) 2 SO1 AB |
|
||
|
На основании теоремы о проекции плоской |
||||||
|
|
|
|||||
O1 |
|
|
фигуры: |
S |
S |
cos( ) |
|
|
|
F |
OA1B1 |
O1AB |
|
1 |
|
|
|
|
|
||||
Mz ( F ) MO1 ( F ) cos( 1 ) MO1z ( F )
MO α





 M
M
O 


 A
A
A1
|
Момент |
силы |
относительно |
оси |
|
равен |
проекции на эту |
ось |
|
B1 |
векторного |
момента |
силы |
|
|
относительно любой точки на оси. |
|||
FS Это утверждение может быть принято в качестве |
||||
определения момента силы относительно оси. |
продолжения |
|||
|
|
|
|
Щелчок для |
