
- •Система сил, линии действия которых пересекаются в одной точке, называется системой сходящихся сил
- •Система сходящихся сил всегда имеет РАВНОДЕЙСТВУЮЩУЮ.
- •Для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник был замкнутым.
- •Если система из трех непараллельных сил находится в равновесии, то линии их действия
- •Если система из n сил находится в равновесии и все силы, кроме одной
- •Невесомая балка длиной 10м расположена на двух шарнирных опорах (неподвижной и подвижной) и
- •Груз весом 1000Н подвешен к вертикальной стене на стержневом кронштейне и находится в
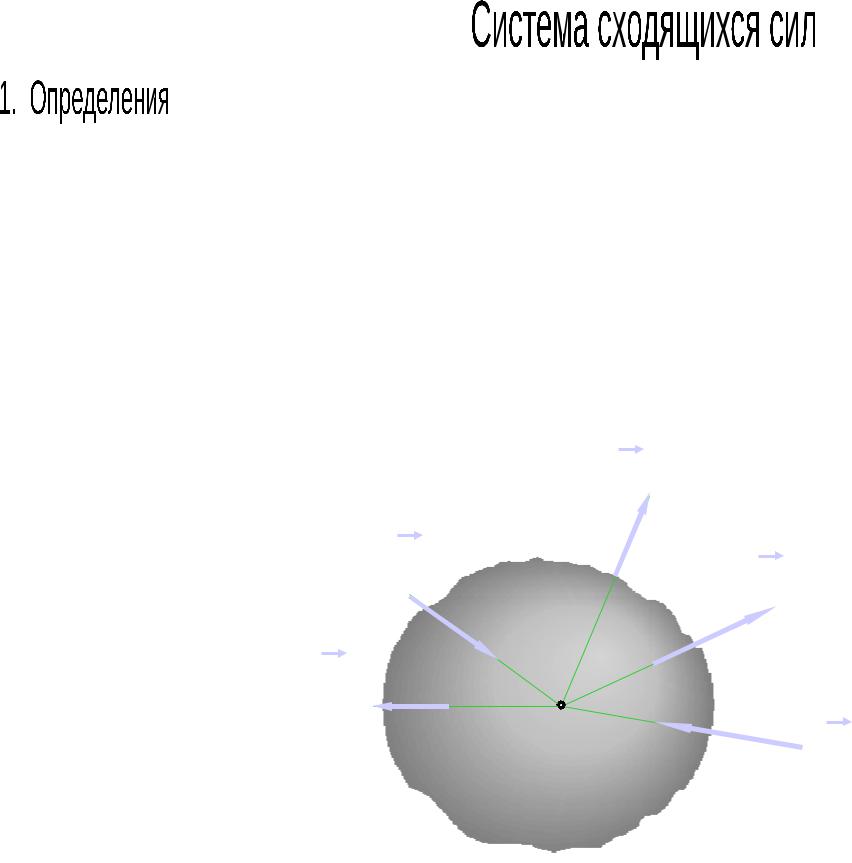
Система сил, линии действия которых пересекаются в одной точке, называется системой сходящихся сил (ССС).
Точка пересечения линий действия всех сил системы называется центром системы сходящихся сил.
F2
F3 |
F1 |
|
F4
C
Fn

Система сходящихся сил всегда имеет РАВНОДЕЙСТВУЮЩУЮ.
|
На основании 4-й аксиомы и 1-го следствия из 2-й аксиомы, приведение системы сходящихся сил |
||||||||||||||||
|
к простейшей (к одной силе – РАВНОДЕЙСТВУЮЩЕЙ) осуществляется последовательным |
||||||||||||||||
|
сложением пар векторов (формальное сложение векторов по правилу параллелограмма или |
||||||||||||||||
|
многоугольника). |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
F1 ,...,Fn R; R |
Fi |
,RF12 |
,RF32 ,RF34 |
,...,FRn |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
||||
|
F2 |
|
|
|
Исходная система сил: |
|
|
- главный вектор системы |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
R1 |
|
n |
F1 |
|
|
i 1 |
|
|
|
|
|
n |
||||
|
|
|
,F2 R1n |
|
|
|
|
|
|||||||||
|
|
|
|
|
Проекции главного вектора на оси координат: |
||||||||||||
F3 |
F2 |
R3 |
F1 |
F1R2 |
Rx Fxi ; Ry Fyi ; |
Rz Fzi |
|||||||||||
|
F |
|
i 1 |
R1 |
,F3 R2 |
|
|
|
|
i 1 |
|||||||
|
n |
|
|
|
R2 |
|
|
i 1 |
|
|
|
||||||
|
|
|
|
|
Модуль |
|
,F4 R3 R Rx |
Ry |
Rz |
||||||||
|
C |
|
|
|
|
главного вектора: |
|
|
|
2 |
2 |
2 |
|||||
|
F4 |
|
|
Fn |
|
……… |
|
|
|
|
|
|
|||||
|
F3 |
|
|
|
Направляющие косинусы: |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
R |
|
|
,Fn |
R |
R |
|
|
|
Rx |
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
Rn 2 |
|
|
cos R . |
|||||||
|
|
|
|
|
cos R ; |
cos |
R ; |
||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
x |
|
|
|
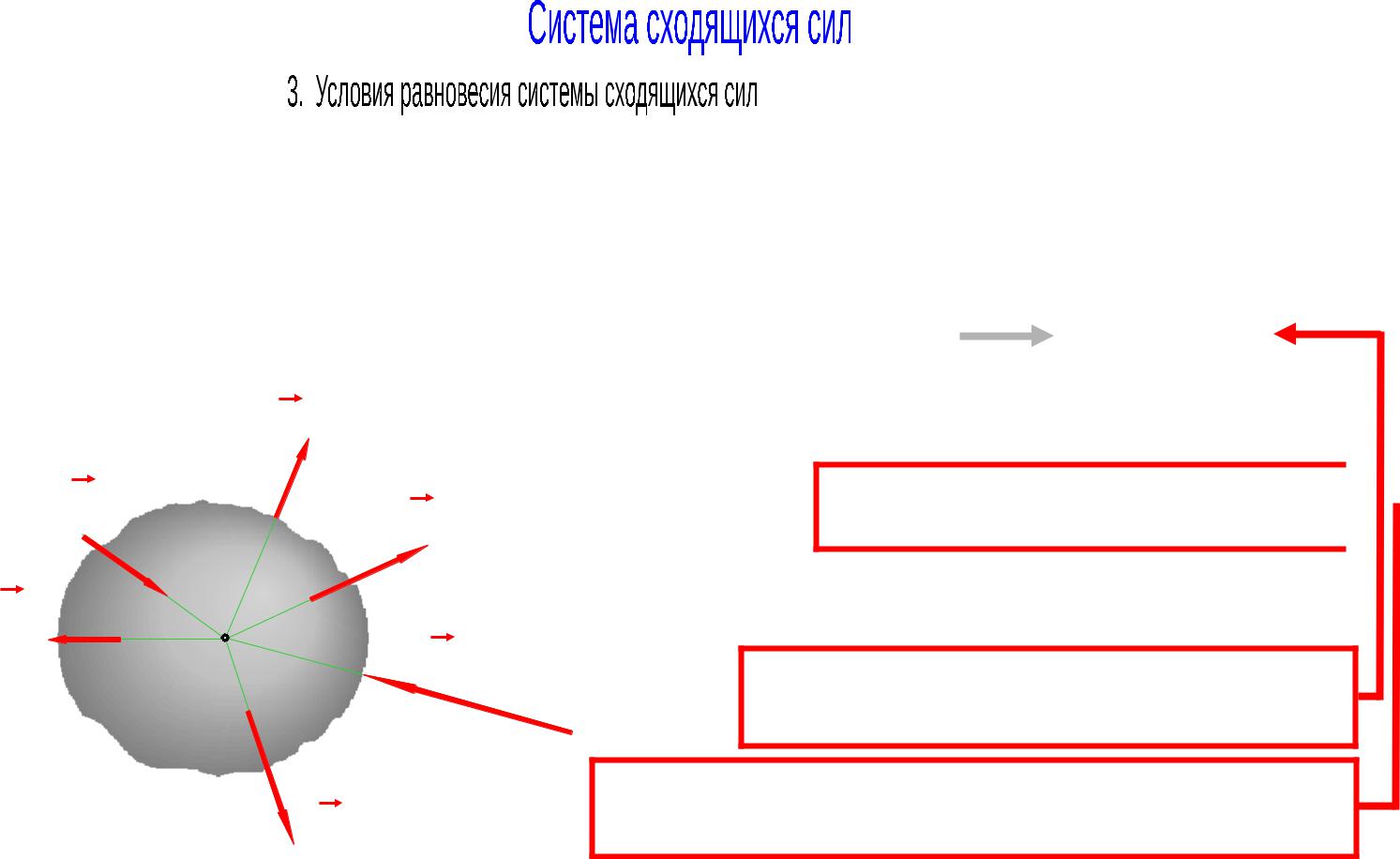
Для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник был замкнутым. Это означает равенство нулю главного вектора, а значит, и равнодействующей.
F2
F3 |
F1 |
|
C |
F6 |
|
F5
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
R 0 |
|
Fi |
0 |
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
Впроекциях на координатные оси:
Fx 0; Fy 0; Fz 0; 

Условия равновесия системы:
В векторной форме: главный вектор системы должен быть равен нулю
В алгебраической форме: сумма проекций всех сил на каждую ось координат равнялась нулю
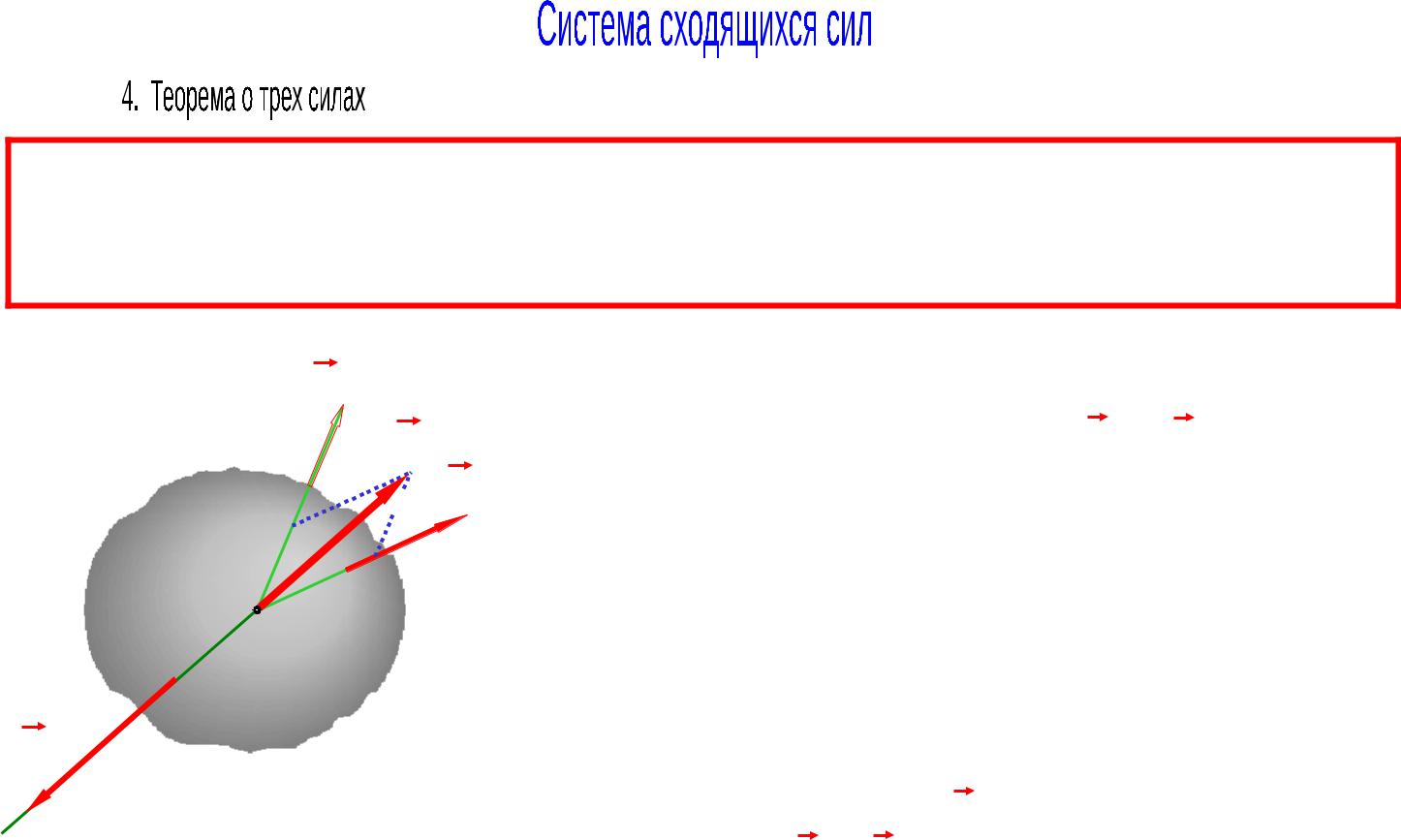
Если система из трех непараллельных сил находится в равновесии, то линии их действия пересекаются в одной точке и силы располагаются в одной плоскости.
F2
 R1
R1

 1
1
C
F3
R1 F1 ,F2 ; F1 ,F2 ,F3 R1 ,F3 .
Система из двух оставшихся сил R1 и F3 находится в
равновесии, т.е. эквивалентна нулю:
R1 ,F3 0.
На основании аксиомы 1 только две равные по модулю, противоположно направленные и действующие по одной прямой силы могут образовывать систему, эквивалентную нулю. Значит, линия действия силы F3
проходит через точку пересечения сил F1 и F2 .
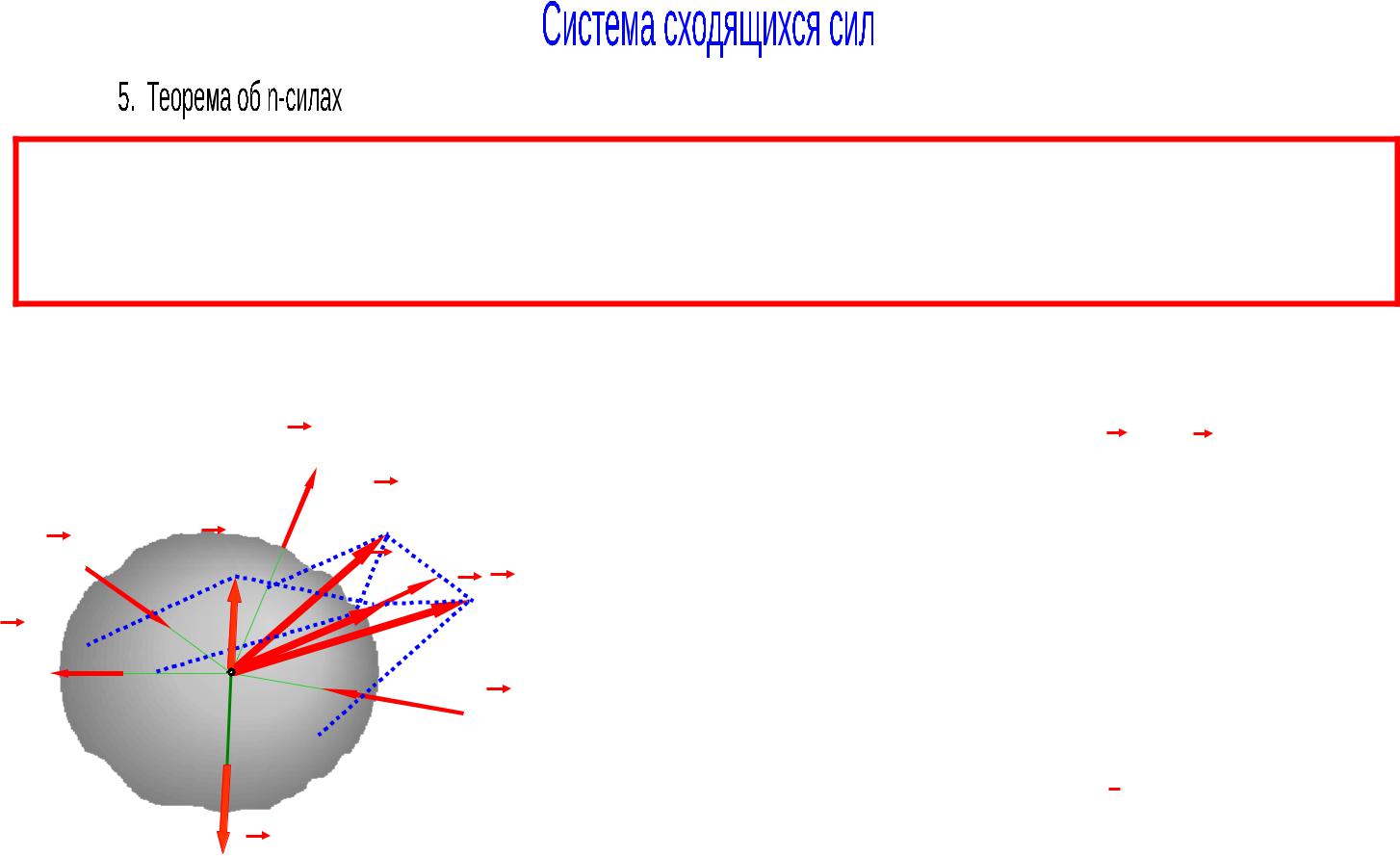
Если система из n сил находится в равновесии и все силы, кроме одной сходятся в одной точке, то и последняя сила проходит через точку схождения всех остальных сил.
|
|
|
F2 |
|
|
|
Rk |
R1 |
|
F |
3 |
R3 |
F1R2 |
|
|
|
|||
|
|
|
||
|
|
|
|
C
Fn-1
F1 ,...,Fn 1 Rk
Система из двух оставшихся сил Rk и Fn находится в
равновесии, т.е. эквивалентна нулю:
Rk ,Fn 0
На основании аксиомы 1 только две равные по модулю, противоположно направленные и действующие по одной прямой силы могут образовывать систему, эквивалентную нулю. Значит, линия действия силы F n проходит через
n проходит через
Fn |
точку пересечения остальных сил. |
|
|
|
|
|
|
|
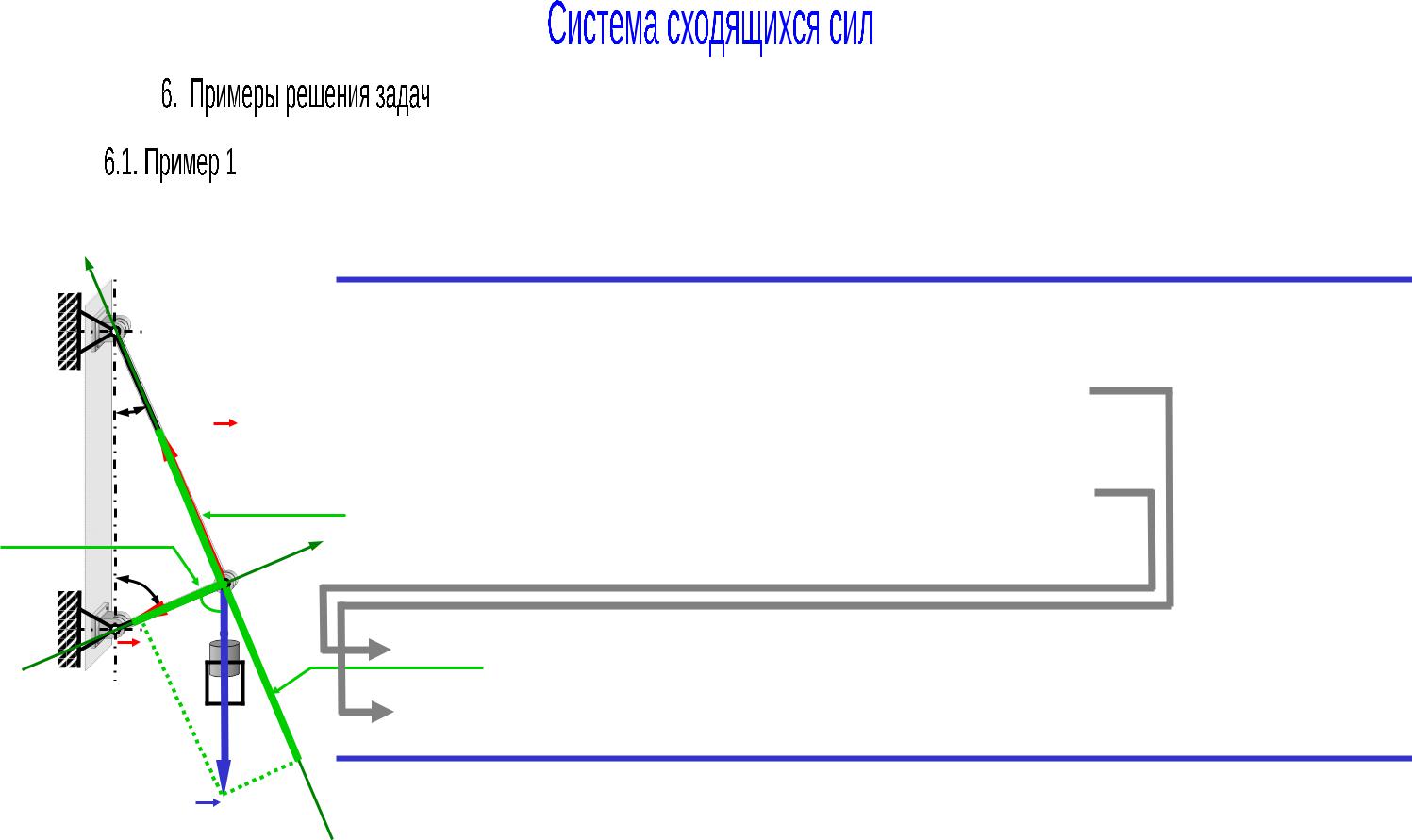
Груз весом 1000Н подвешен к вертикальной стене на составном кронштейне и находится в |
|||||||||||
|
|
|
|
|
|
|
равновесии. Углы, образуемые стержнями кронштейна с вертикалью – 300 (для верхнего |
|||||||||||
y |
|
|
|
|
|
|
стержня) и 600 – (для нижнего). |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
Определить усилия в верхнем и нижнем стержнях. |
|
|
|
|||||||||
|
|
A |
|
|
|
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
F |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
Xi |
̶UPcos60 ̶U |
= 0 ; |
|
|
||||||
|
|
|
300 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
RAC RACy = RAC |
|
n |
F |
|
0 |
̶U |
|
|
RBC |
= 0 ; |
|
|
|||
PR |
= -=Pcos60-R |
0 |
x |
|
i 1 Yi |
: |
|
|
+ RAC |
|
|
|||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
||||||
BCx BC |
|
|
|
Решение уравнений |
равновесия: |
|
|
|
||||||||||
|
|
60 |
|
|
|
|
|
|
|
|
||||||||
|
|
0 |
|
|
|
Psin60 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
RBC |
600 |
P = -Psin600 |
P sin60 |
0 |
1000 0.866 866H ; |
|
|||||||||||
|
|
|
y |
RAC |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
P cos600 |
1000 0.500 500H ; |
||||||||
|
|
|
|
|
|
|
BC |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
|
|
|
|
|
|
|
|
Знак «–» показывает, что реакция |
||
|
|
|
P |
|
|
|
RAC 866 H , RBC 500H |
направлена |
в |
сторону, |
||||||||
|
|
|
|
|
|
расчетной схеме. |
|
показанной на |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
противоположную |
|
|
А T 1
1
c
10 м |
м |
|
D T2 |
0.1 |
|
B |
||
C |
E |
|
P |
||
0.1м |
T2 b P
P
T1 e
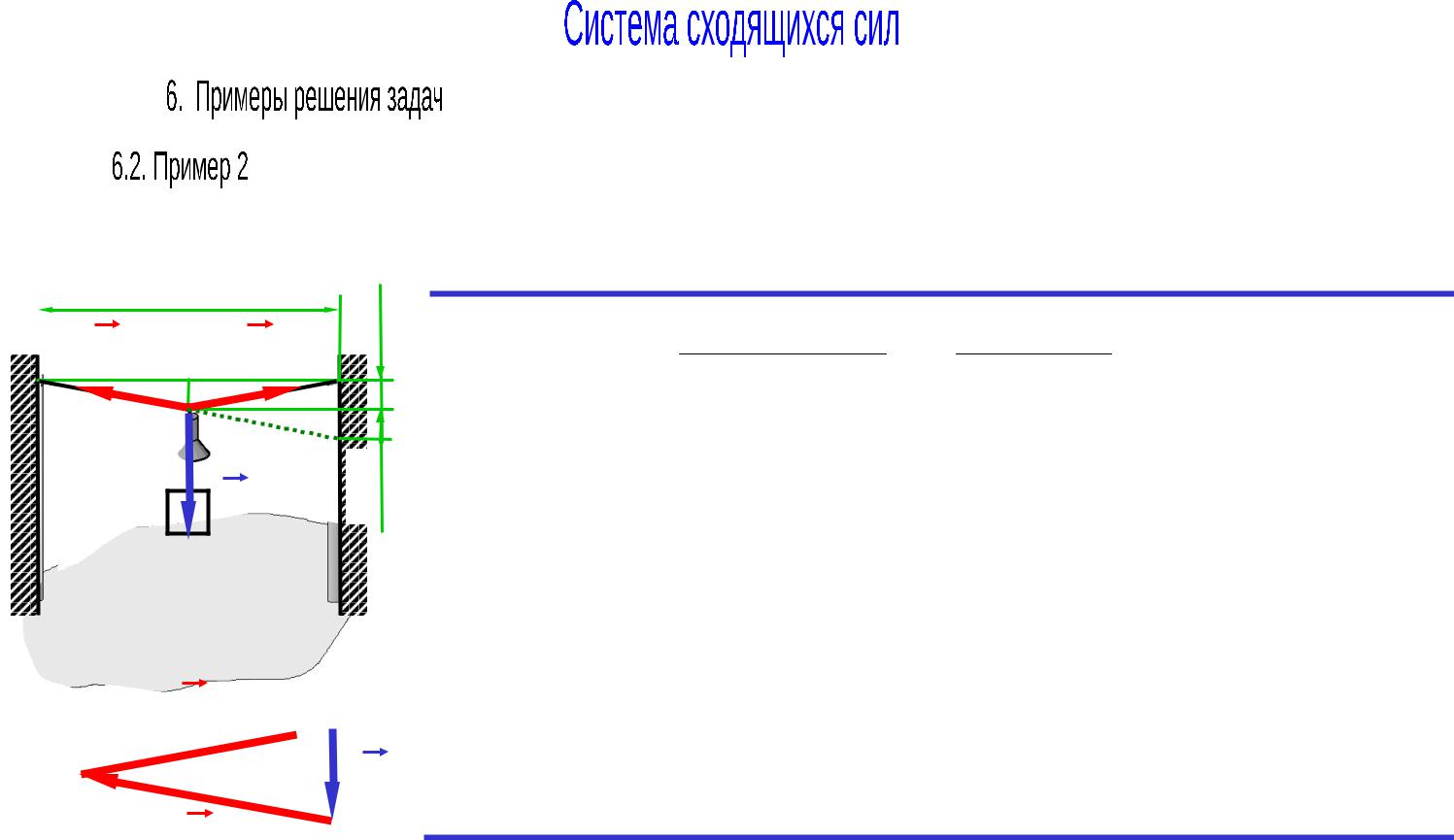
Фонарь уличного освещения весом 100Н подвешен на тросе посредине между двумя вертикальными столбами, так, что величина провеса троса в точке подвеса фонаря составляет 0.1м. Расстояние между столбами 10м.
Определить силы натяжения в ветвях троса.
Решение:
CE BC 
 DC 2 BD2
DC 2 BD2 
 0.12 52 5.001м
0.12 52 5.001м
Треугольники СВЕ и cbe (силовой) подобны по признаку параллельности сторон (CB||cb, BE||be, CE||ce), следовательно
выполняются соотношения: |
|
|
|
|
|
|
||||||
|
be |
|
ce |
|
cb |
или |
P |
|
T1 |
|
T2 |
; |
|
BE |
CE |
CB |
|
|
|
||||||
|
BE |
CE |
CB |
|||||||||
T |
|
P CE |
100 5.001 2500.5H ; |
||
|
|
|
|||
1 |
|
|
BE |
0.5 |
|
|
|
|
|||
T |
P CB |
|
100 5.001 2500.5H . |
||
|
|||||
2 |
|
|
BE |
0.5 |
|
|
|
|
|||
Ответ: |
T1 2500.5H , T2 2500.5H |
||||
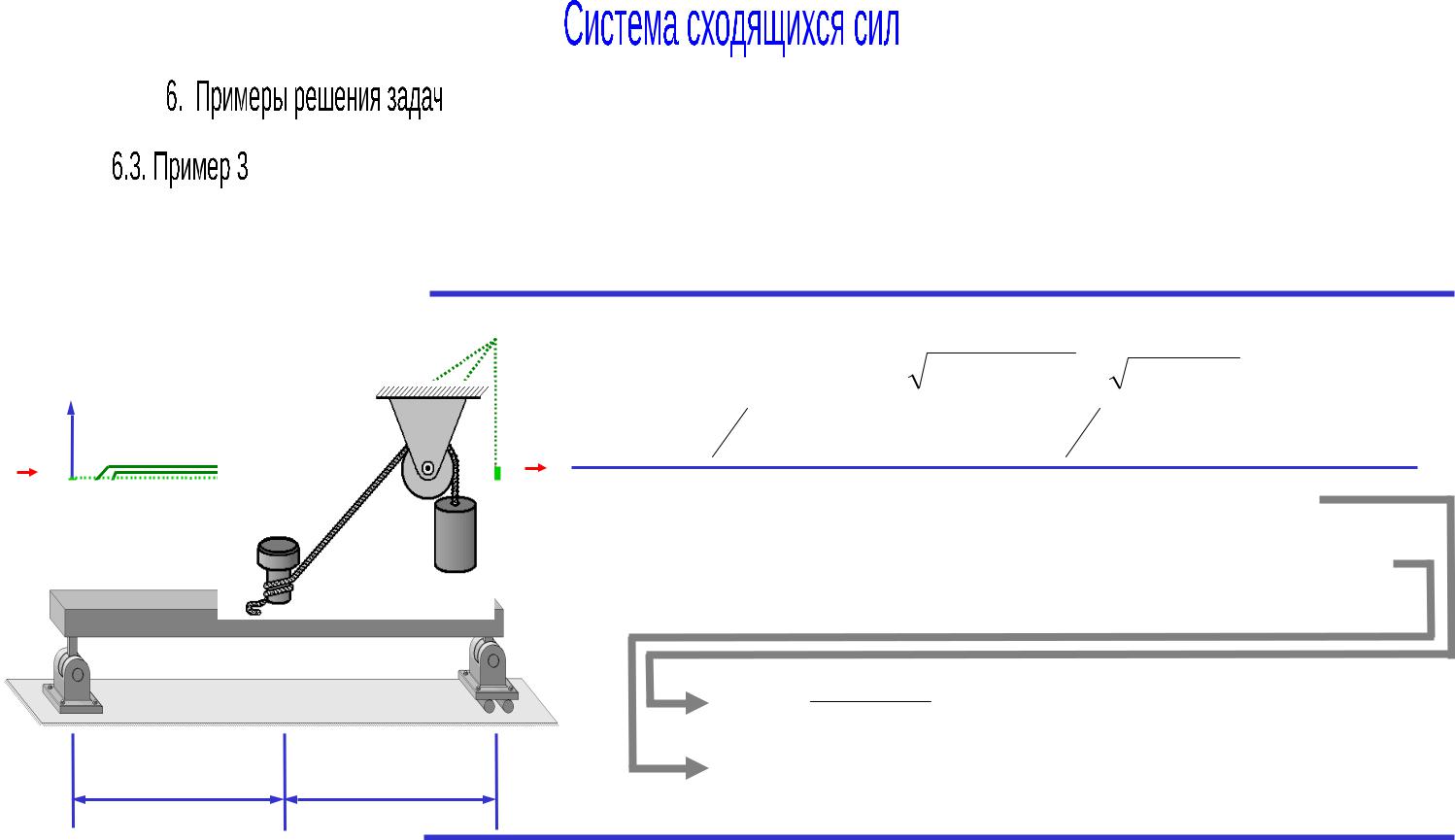
Невесомая балка длиной 10м расположена на двух шарнирных опорах (неподвижной и подвижной) и находится в равновесии. В середине балки прикреплен трос подвешенного на блоке груза весом 1000Н. Угол наклона троса к горизонту 450.
Определить реакции шарниров балки.
|
|
|
D |
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AB2 BD2 |
|
|
|
|
|
||
y |
|
|
|
BD BC 5 м; |
|
AD |
|
|
100 25 11 .18 м; |
|||||||||
|
|
|
sin BD |
|
|
|
0 .447 ; |
cos AB |
|
|
0 .894; |
|||||||
Py=Psin45 |
0 |
|
|
AD |
AD |
|||||||||||||
RAy=RAsinα |
|
|
in 1 FXi |
0 : RA cos P cos450 |
0; |
|||||||||||||
|
|
|
|
|||||||||||||||
|
|
|
|
B in 1 FYi |
0 : RA sin P sin450 |
RB 0. |
||||||||||||
|
|
|
|
Решение уравнений равновесия: |
|
|
|
|
|
|
||||||||
|
|
|
|
RA |
P cos 450 |
|
1000 0.707 |
790.83H ; |
||||||||||
|
|
|
|
|
cos |
0.894 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5 м |
|
5 м |
|
R |
B |
R |
A |
sin P sin450 |
|
|
|
|
|
|||||
|
|
|
|
790.83 0.447 1000 0.707 353.50H |
||||||||||||||
|
|
|
|
Ответ: |
|
|
RA 790.83H , |
RB 353.50H |
||||||||||
|
|
|
|
|
|
|
||||||||||||
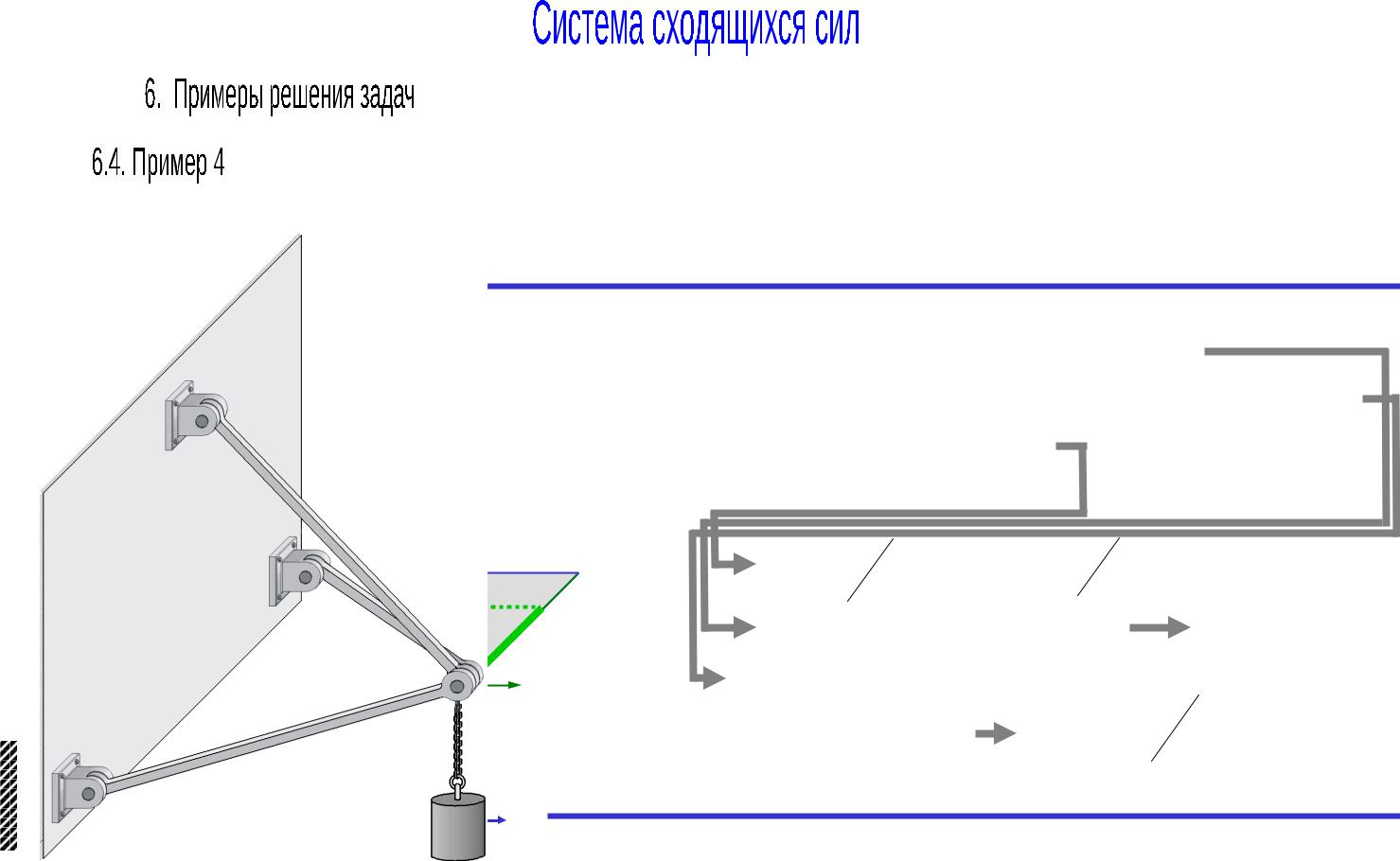
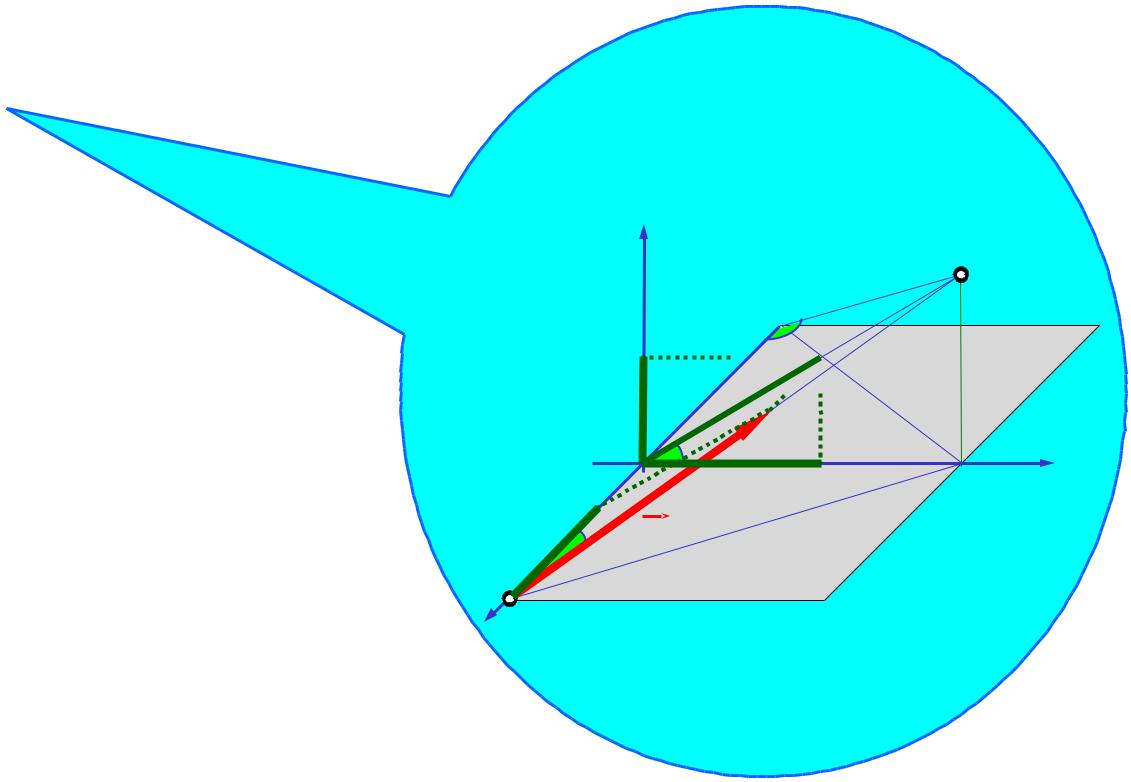
Груз весом 1000Н подвешен к вертикальной стене на стержневом кронштейне и находится в равновесии. Стержни скреплены между собой и прикреплены к стене посредством шарниров. Углы, образуемые стержнями со стеной, равны 450.
Определить реакции стержней кронштейна.
Решение: |
|
|
|
|
|
|
|
|
in 1 FXi 0 : |
RA cos450 RC cos 450 |
0; |
|
|||||
in 1 FYi 0 : |
RA sin450 RB sin450 |
RC sin450 0; |
||||||
in 1 FZi 0 : |
RB cos 450 P 0. |
|
|
|
|
|||
Решение уравнений равновесия: |
|
|
|
|
|
|
||
|
R |
P |
|
1000 |
0.707 |
1414.43H ; |
||
|
B |
cos450 |
|
|
||||
RCx= - RCcos450 |
RA cos 450 |
RC cos 450 ; |
|
RA RC ; |
||||
|
RA sin450 |
RB sin450 |
|
RA sin450 |
||||
=0=0 |
|
|
|
RA |
RB |
|
707.22H ; |
|
AxBxy=RAcos450 2RA RB sin450 0; |
2 |
|||||||
RA RC 707.22H |
|
|
|
|
|
|||
|
|
|
|
|
|
|||
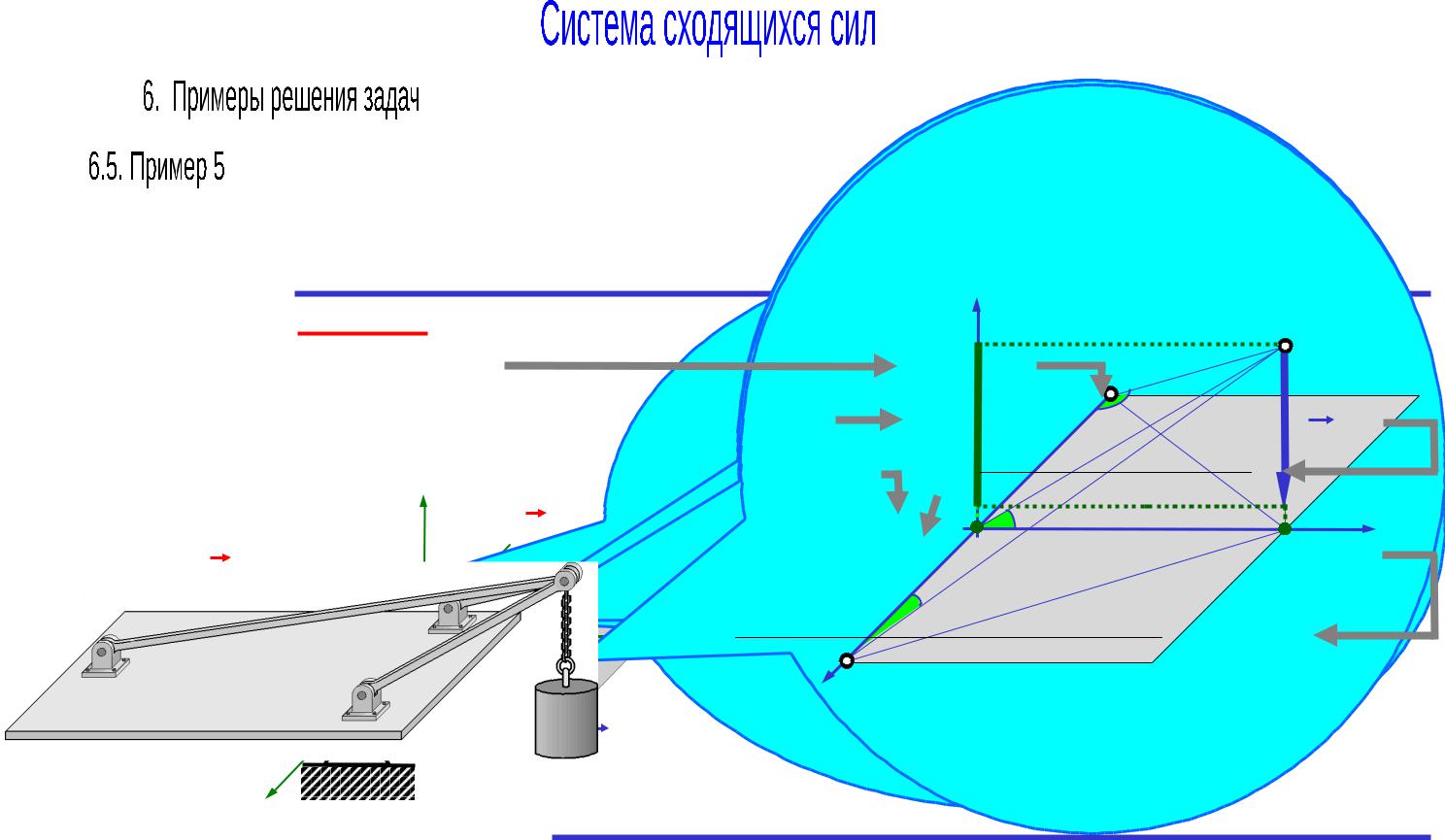
Ответ: RA 707.22H , RB 1414.43H , RC 707.22H .
|
|
|
|
Груз весом 1кН |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
стержней в точках |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
BD и AD – 450. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
||
in 1 FXi 0 : RA cos 450 RB cos 450 0; |
|
|
|
|
|
|
|
|
|
|
|
|
RA |
RB ; |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|||||||||||||||||
n |
F 0 : R cos15 |
0 R |
|
sin450 cos 300 R |
sin450 cos 30 |
0 0; |
|
|
R |
|
cos150 |
|
450 |
|
sin450 cos300 |
0; |
||||||||||||||||||||||
|
A |
|
|
|
|
2R |
A |
|||||||||||||||||||||||||||||||
i 1 Yi |
C |
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
Pz= - CP |
|
|
|
|
|
|
|
|
|
|
0P |
|
|||||||||
n |
|
|
0 |
RA sin45 |
0 |
sin30 |
0 |
sin45 |
0 |
sin 30 |
0 |
P 0; |
RC |
|
|
|
2RA sin450 cos 30 |
|
||||||||||||||||||||
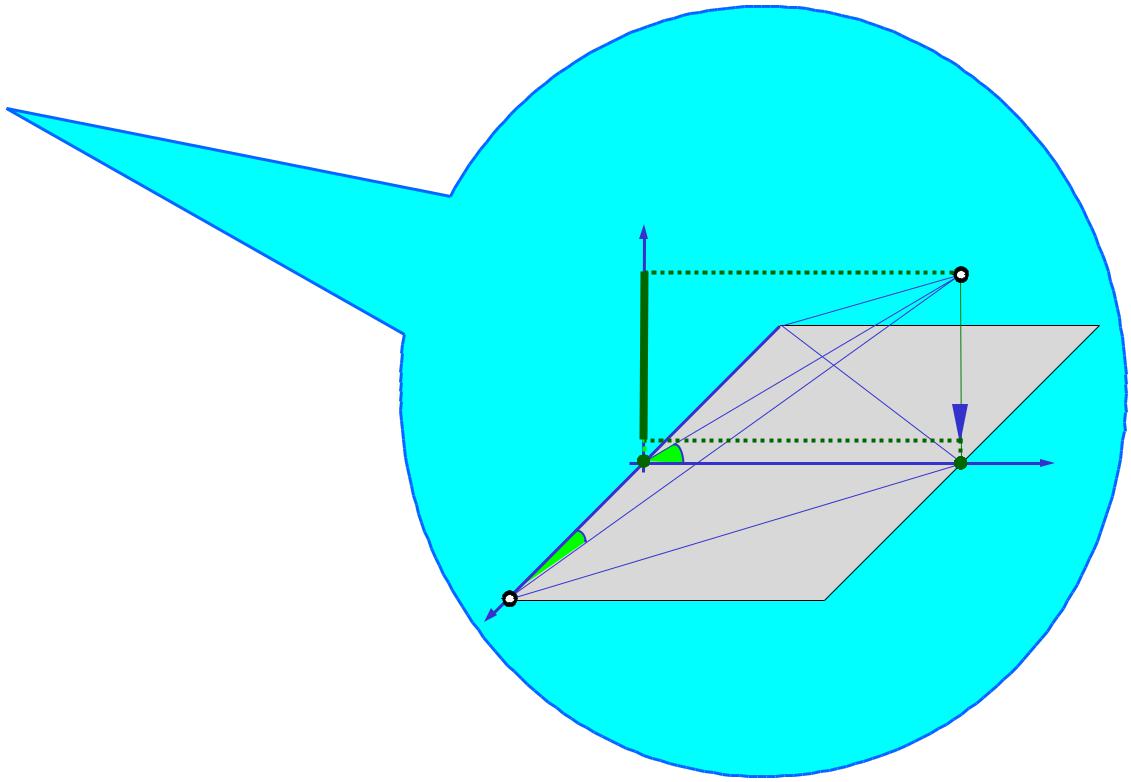
i 1 FZi 0 : RC sin15 |
|
|
RB |
|
|
|
|
|
|
|
cos15 |
0 |
|
|
; |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
||||
|
|
|
|
|
|
|
|
|
|
|
2RA sin45 |
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
cosP30=0 |
300 |
0 |
2RA sin45 |
0 E |
|
0 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
cos15 |
|
|
|
x |
sin15 |
|
sin30 |
|
P 0; |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
450 |
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
Py=0 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
RA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.64кН ; |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
0 |
(sin30 |
0 |
|
cos 30 |
0 |
tg15 |
0 |
) |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 sin45 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
RB RA 2.64кH ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
x |
|
|
|
|
|
|
|
RC 2 2.64 0.707 0.866 |
|
3.35кH ; |
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.966 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Ответ: |
|
RA 2.64H , |
|
|
RB 2.64H , |
|
|
RC 3.35H . |
|||||||||||||||||||||
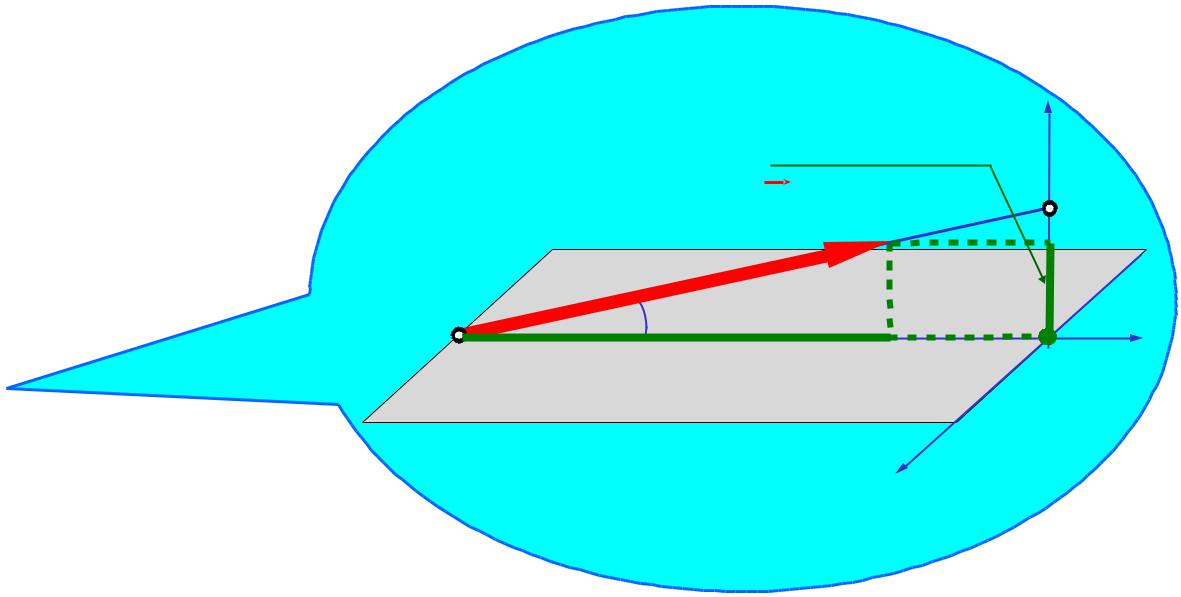
z
RCz=RCsin150
D
RC
C |
|
O |
y |
150 R =R |
cos150 |
|
|
|
R =0 |
||
Cy C |
|
|
|
|
|
|
Cx |
|
x |
|
|
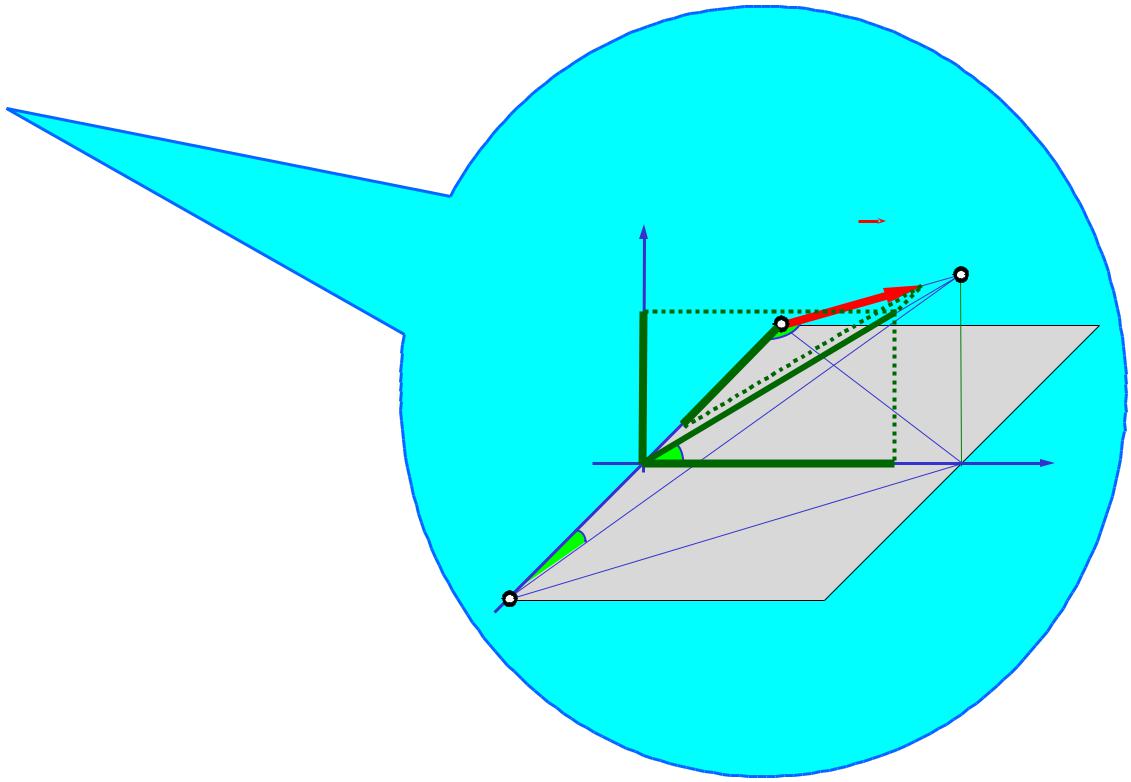
sin300
zsin450 A =R Az R
O
450
|
|
|
0 |
|
|
|
|
|
|
|
|
5 |
RA D |
|
|||
|
|
4 |
|
|||||
|
|
s |
|
|||||
|
|
o |
|
|
|
|
|
|
|
|
Ac |
|
|
|
|
|
|
|
= |
A |
|
|
|
|
0 |
|
|
|
|
|
|
4 |
|
||
|
R450 |
|
|
|
|
|||
|
|
|
|
|
5 |
|
||
|
|
|
|
|
n |
|
||
|
x |
|
|
|
i |
|
|
|
R |
|
|
s |
|
|
|
||
A |
|
|
|
|
|
|||
|
|
A |
|
|
|
|||
|
|
R |
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
= |
|
|
|
|
|
|
|
R |
y |
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
A |
|
|
|
|
y |
|
300 |
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
||
R =R |
sin450cos300 |
|||||||
|
Ay A |
|
|
|
|
|
|
|
x
B 
R x
|
|
|
sin300 |
|
|
|
|
|
sin450 |
|
|
|
|
z |
|
|
|
|
|
|
|
B |
|
|
|
|
=R |
|
|
|
|
|
|
0 |
|
|
|
|
5 |
|
|
|
|
|
4 |
|
|
|
|
s |
Bz |
|
|
|
|
|
|
||
|
|
o |
|
|
|
|
c |
R |
|
||
|
R |
BO |
|
|
|
- |
|
|
|||
|
|
30 |
|
||
= |
|
|
|
|
0 |
|
|
|
|
|
|
x |
|
|
|
RB |
|
B |
450 |
|
|
||
|
|
|
|
||
|
B |
|
|
|
|
D
A
450 











 RBzy=RBsin450
RBzy=RBsin450
R =R |
E |
y |
|
||
sin450cos300 |
||
By B |
|
|
z
D
A
Pz= - P 450 
P

O |
|
y |
P =0 300 |
E |
|
x |
|
Py=0 |
|
|
|
450 |
|
|
x
B
