подгон 2018 (легендарный) / 1 семестр / Практикум по линейной алгебре в Matlab / ЛИНАЛ / Линейная Алгебра / Модуль 2_Занятие 7(2) Плоскость и прямая в пространстве

Занятие 7 (2). Уравнения прямых и плоскостей в пространстве.

Поверхность в пространстве рассматривается как геометрическое место точек, удовлетворяющих какому-либо условию. Уравнением поверхности в прямоугольной системе координат называется такое уравнение , которому удовлетворяют координаты каждой точки, принадлежащей поверхности, и не удовлетворяют координаты точек, не принадлежащих этой поверхности. Простейшей поверхностью является плоскость.

Н

ормальным вектором плоскости называется любой ненулевой вектор, перпендикулярный этой плоскости. Пусть – нормальный вектор плоскости и – фиксированная точка плоскости (см. рис. 1).

Рис.1.

Точка пространства принадлежит плоскости тогда и только тогда, когда а значит,

(1)

(векторное уравнение плоскости). Из уравнения (1) ввиду того, что мы получаем уравнение плоскости в виде

(2)

или

(3)

где

Для того, чтобы составить уравнение плоскости, обычно находят её нормальный вектор и какую-нибудь точку. После этого записывают уравнение в виде (2). Раскрывая скобки и приводя подобные члены, получают уравнение в виде (3).

Если известны длины отрезков, отсекаемых плоскостью от осей координат, то уравнение плоскости пишется сразу:

(4)

(уравнение плоскости “в отрезках”).

В МАТЛАБ плоскость (поверхность) можно изображать с помощью различных функций: plot3(), mesh(),surf(),surfl().Общим для всех этих функций является необходимость использовать функцию meshgrid. Посмотрите в help как они устроены. А также читайте Кривиёва стр. 153... Последние три функции позволяют добиться большей реалистичности изображения трехмерных графиков.

В примере 1 мы построим плоскость по общему уравнению с помощью этих различных функций. В этом же примере мы познакомимся также с функцией view(,). Прочтите в help и/или в Кривилёве на стр.151 как она работает.

Пример 1. Построить плоскость, заданную общим уравнением . Вывести обозначения осей заголовок координатного пространства. Изобразить также нормальный вектор к этой прямой, выходящим из начала координат.

Общее уравнение плоскости

A = 3; B = 4; C = -4; D = -12;

% задаем координаты узлов пространственной сетки

x = -4:0.4:4; y = -3:0.5:3;

% создаем матрицы, содержащие координаты узлов пространственной сетки

[X,Y]=meshgrid(x,y);

Z = (-A*X-B*Y-D)/C;

figure

hold on

% пометим узловые точки круговыми маркерами

plot3(X,Y,Z,'or','MarkerSize',8)

% график будет перенасыщен кружочками, попробуйте вывести график без этих кружочков

plot3(X,Y,Z)

xlabel('x'), ylabel('y'), zlabel('z')

title('3x + 4y - 4z - 12 = 0')

line([0;3],[0;4],[0;-4], 'LineWidth',4 ) % строим нормальный вектор

line([-5 0 0;5 0 0],[ 0 -5 0;0 5 0],[ 0 0 -5;0 0 5], 'LineWidth',3, 'Color', 'black' )

box on,axis equal, axis square, grid on

view(-37,39)

>> figure

hold on

% пометим узловые точки круговыми маркерами черного цвета

plot3(X,Y,Z,'ok')

mesh(X,Y,Z)

% график будет перенасыщен кружочками, попробуйте вывести график без этих кружочков

xlabel('x'), ylabel('y'), zlabel('z')

title('3x + 4y - 4z - 12 = 0')

line([0;3],[0;4],[0;-4], 'LineWidth',4 ) % строим нормальный вектор

line([-5 0 0;5 0 0],[ 0 -5 0;0 5 0],[ 0 0 -5;0 0 5], 'LineWidth',3, 'Color', 'black' )

box on,axis equal, axis square, grid on

view(-37,39)

>> figure

hold on

% пометим узловые точки круговыми маркерами

plot3(X,Y,Z,'om','MarkerSize',8)

surf(X,Y,Z)

% график будет перенасыщен кружочками, попробуйте вывести график без этих кружочков

xlabel('x'), ylabel('y'), zlabel('z')

title('3x + 4y - 4z - 12 = 0')

line([0;3],[0;4],[0;-4], 'LineWidth',4 ) % строим нормальный вектор

line([-5 0 0;5 0 0],[ 0 -5 0;0 5 0],[ 0 0 -5;0 0 5], 'LineWidth',3, 'Color', 'black' )

box on,axis equal, axis square, grid on

view(-37,39)

>> figure

surfl(X,Y,Z)

xlabel('x'), ylabel('y'), zlabel('z')

title('3x + 4y - 4z - 12 = 0')

line([0;3],[0;4],[0;-4], 'LineWidth',4 ) % строим нормальный вектор

line([-5 0 0;5 0 0],[ 0 -5 0;0 5 0],[ 0 0 -5;0 0 5], 'LineWidth',3, 'Color', 'black' )

box on,axis equal, axis square, grid on

>> figure

surf(X,Y,Z)

shading interp %убирает сетку на плоскости и делает плавный переход цвета

xlabel('x'), ylabel('y'), zlabel('z')

title('3x + 4y - 4z - 12 = 0')

line([0;3],[0;4],[0;-4], 'LineWidth',4 ) % строим нормальный вектор

line([-5 0 0;5 0 0],[ 0 -5 0;0 5 0],[ 0 0 -5;0 0 5], 'LineWidth',3, 'Color', 'black' )

box on,axis equal, axis square, grid on

>> figure

surfl(X,Y,Z)

shading interp %убирает сетку на плоскости и делает плавный переход цвета

xlabel('x'), ylabel('y'), zlabel('z')

title('3x + 4y - 4z - 12 = 0')

line([0;3],[0;4],[0;-4], 'LineWidth',4 ) % строим нормальный вектор

line([-5 0 0;5 0 0],[ 0 -5 0;0 5 0],[ 0 0 -5;0 0 5], 'LineWidth',3, 'Color', 'black' )

box on,axis equal, axis square, grid on

Для того чтобы проще было понять роль функции meshgrid рассмотрим более простой пример 2 с выводом всех табличек на экран.

Пример 2.

A = 3; B = 4; C = -4; D = -12;

% задаем координаты узлов пространственной сетки

x = -1:1:1, y = 0.5:0.5:1,

[X,Y]=meshgrid(x,y),

Z = (-A*X-B*Y-D)/C,

plot3(X,Y,Z,'or','MarkerSize',8, 'LineWidth',4), box on

xlabel('x'), ylabel('y'), zlabel('z')

title('3x + 4y - 4z - 12 = 0')

hold on

surf(X,Y,Z)

% сначала посмотрите программу без view, затем вручную поверните график, так чтобы было видно все 6 узловых точек, в левом нижнем углу графического окна вы увидите нужные

параметры (Az: -65 El: 30) для функции, затем их можно вставить в программу, чтобы картинка выводилась сразу с выигрышной точки обзора.

view(-65,31)

% массив абсцисс состоит из трех точек

x =

-1 0 1

% массив ординат из двух точек

y =

0.5000 1.0000

% Двумерный массив Х 2х3 для каждой узловой точки сетки

X =

-1 0 1

-1 0 1

% Двумерный массив У 2х3 для каждой узловой точки сетки

Y =

0.5000 0.5000 0.5000

1.0000 1.0000 1.0000

% Двумерный массив Z 2х3 для значений функции Z=f(X,Y) в каждой узловой точки сетки

% Z=f(X,Y) понимается как функция двух переменных.

Z =

-3.2500 -2.5000 -1.7500

-2.7500 -2.0000 -1.2500

Функция plot3 выводит круговые маркеры в узловых точках сетки, в точках с координатами (X,Y,Z).

Функция surf закрашивает каждую клетку плоскости (поверхности) определенным цветом, который зависит от значений элемента массива Z. При этом из четырех узловых точек, ограничивающих клетку, выбирается и учитывается минимальная по значению. Изменение цвета на плоскости (поверхности) означает изменение по оси аппликат (высоте, глубине).

Упражнение 1

Задача. Составить уравнение плоскости (в отрезках), отсекающей на осях и отрезки, соответственно равные 5 и 7, и проходящей через точку .

Построить плоскость. Построить нормальный вектор.

В координатном пространстве построить черным цветом толщиной два пункты оси x,y и z, на которых в местах пересечений с плоскостью вывести круговые маркеры синего цвета и обозначить координаты точек пересечения плоскости с осями координат. Вывести обозначение осей и заголовок координатного пространства, в котором написать уравнение плоскости в отрезках.

Направляющим вектором прямой называется любой ненулевой вектор, коллинеарный этой прямой. Пусть – направляющий вектор прямой и – фиксированная точка прямой (см. рис. 2).

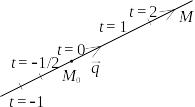
Рис.2.

Точка пространства принадлежит прямой тогда и только тогда, когда векторы и коллинеарны, а значит, для некоторого выполняется равенство

(5)

(векторное уравнение прямой). Подставив в (5) координаты векторов и точек, получим уравнение прямой в виде

(6)

(каноническое уравнение прямой)

или в виде

(7)

(параметрические уравнения прямой).

Упражнение 2

Задача. Найти с помощью МАТЛАБ угол Phi между плоскостями и . (Угол между плоскостями – это угол между их нормальными векторами. Ответ. )

Построить линию, являющуюся пересечением двух плоскостей, заданных общими уравнениями.(То есть построить обе плоскости). Построить нормальные векторы к плоскостям из точки М принадлежащей обеим плоскостям. Найти направляющий вектор прямой, построить его из начала координат и из точки М. Составить каноническое уравнение прямой и вывести его в названии к графику. (см задачу 12)

Ниже приводятся решения типовых задач на прямые и плоскости в пространстве, которые нужно изучить и прикинуть, как вы будете их визуализировать и обрабатывать в среде МАТЛАБ. По поводу визуализации особенно трехмерных графиков почитайте Кривилёва. Познавать потрясающие возможности высокоуровневой и низкоуровневой (дескрипторной) графики МАТЛАБ можно (и нужно) очень долго. Предлагаю изучать это самостоятельно. Нам сейчас главное уметь интерпретировать типовые задачи аналитической геометрии для более глубокого понимания самой геометрии.

Теория в типовых задачах.

Перечислим ряд типовых задач на прямые и плоскости в пространстве, которые необходимо научиться решать студенту, изучающему аналитическую геометрию.

1. Составлять уравнение плоскости, проходящей: через три заданные точки, через прямую и точку, через две пересекающиеся прямые, через две параллельные прямые.

2. Составлять уравнение прямой, проходящей через две данные точки, являющейся линией пересечения двух данных плоскостей.

3. Составлять уравнение плоскости, проходящей через данную точку параллельно данной плоскости, перпендикулярно данной прямой, через две точки параллельно данной прямой, через точку параллельно двум прямым.

4. Составлять уравнение прямой, проходящей через заданную точку параллельно заданной прямой, перпендикулярно заданной плоскости.

5. Находить точку пересечения прямой и плоскости, двух данных пересекающихся прямых.

6. Выяснять взаимное расположение двух прямых, двух прямых, двух плоскостей, трёх плоскостей, прямой и плоскости.

7. Находить расстояние между двумя точками, между двумя параллельными прямыми или плоскостями, от точки до прямой, от точки до плоскости, между двумя скрещивающимися прямыми.

8. Проектировать точку на прямую, на плоскость, прямую на плоскость.

9. Находить точку, симметричную данной точке относительно данной точки, данной прямой, данной плоскости.

10. Составлять уравнение прямой (или плоскости), симметричной данной прямой (соотв., плоскости) относительно данной точки, данной прямой, данной плоскости.

11. Находить углы между двумя прямыми, двумя плоскостями, прямой и плоскостью.

12. Использовать понятие отклонения для определения, “с какой стороны” от прямой или плоскости находится точка.

Задача 1. Даны точки и Составить уравнение плоскости, проходящей через точку перпендикулярно отрезку

Решение. В качестве нормального вектора плоскости можно взять вектор а в качестве точки плоскости – точку Подставив в (2), получим: или

Задача 2. Составить уравнение плоскости, проходящей через точки и

Решение. Вычислим векторы и Нормальный вектор плоскости перпендикулярен этим векторам, поэтому можно взять в качестве нормального вектора их векторное произведение. Имеем:

Взяв в качестве любую из данных точек, например, и подставив в (2), получим: или

Задача 3. Найти угол между плоскостями и

Решение. Угол между плоскостями – это угол между их нормальными векторами. Нормальные векторы найдём из уравнений плоскостей: Следовательно,

Таким образом,

Задача 4. Через точку провести плоскость, параллельную плоскости

Решение. Нормальный вектор данной плоскости будет годиться и для параллельной плоскости. Подставив в формулу (2) получим: или

Задача 5. Составить уравнение плоскости, симметричной плоскости относительно точки

Решение (см. рис. 3). Очевидно, искомая плоскость параллельна плоскости

Рис.3.

Возьмём какую-нибудь точку плоскости например, Тогда а значит, Пусть – начало координат. Имеем: Следовательно, В качестве нормального вектора плоскости можно взять нормальный вектор плоскости т.е. Подставив выбранные значения в формулу (2), получим уравнение плоскости или

Задача 6. Составить уравнение плоскости, симметричной плоскости относительно оси ординат.

Решение. Точка, симметричная точке – это Поэтому уравнение искомой плоскости мы получим, заменив и на и т.е. или

Разберём теперь решения задач на уравнение прямой.

Задача 7. Составить уравнение прямой параллельной прямой и проходящей через точку

Решение. Направляющий вектор для прямой можно взять тот же, что у т.е. Взяв и подставив выбранные значения в уравнение (6), получим:

Задача 8. Составить уравнение прямой, симметричной прямой относительно точки

Решение (см. рис. 4).

Рис.4.

Из уравнения прямой находим какую-нибудь точку прямой например, Если – точка, симметричная точке относительно то поэтому и аналогично Следовательно, Подставив в (4), получим:

Рассмотрим теперь смешанные задачи на плоскость и прямую в пространстве.

Задача 9. Спроектировать точку на прямую

Решение (см. рис. 5).

Рис.5.

Если мы проведём через точку плоскость перпендикулярную прямой то точка пересечения прямой и плоскости и будет проекцией на Возьмём уравнение прямой и обозначим дроби буквой Получим: Отсюда получаем параметрические уравнения прямой

(8)

Составим теперь уравнение плоскости Так как прямая и плоскость перпендикулярны, то в качестве нормального вектора плоскости можно взять направляющий вектор прямой, т.е. Отсюда по формуле (2) получаем уравнение плоскости или Подставим в это уравнение формулы (8), получим: Подставляя это значение в формулы (8), получим координаты точки т.е.

Задача 10. Составить уравнение медианы треугольника если

Решение. Учащихся не должно смущать то обстоятельство, что треугольник задан в четырёхмерном пространстве. Позже в курсе линейной алгебры будут изучаться произвольные п-мерные пространства для любого натурального и даже бесконечномерные пространства. Уравнения прямых в п-мерном пространстве – такие же, как в трёхмерном.

Найдём середину отрезка

В качестве направляющего вектора медианы можно взять вектор но лучше взять вектор чтобы координаты были целыми числами: Взяв в качестве точку получим уравнение медианы

Задача 11. Найти точку, симметричную точке относительно плоскости

Решение (см. рис. 6).

Рис.6.

Составим уравнение прямой проходящей через перпендикулярно плоскости Направляющим вектором прямой может служить нормальный вектор плоскости Теперь можно написать параметрические уравнения прямой Подставим эти выражения в уравнение плоскости Отсюда Мы нашли значение параметра для точки т.е. У точки значение параметра равно 0, следовательно, точка симметричная точке относительно будет иметь значение параметра, в 2 раза большее, чем т.е. Подставив в уравнение прямой получим: Таким образом,

Задача 12. Прямая задана как пересечение плоскостей и Написать каноническое уравнение этой прямой.

Решение (см. рис. 7).

Рис.7.

Пусть Из уравнений плоскостей и найдём их нормальные векторы: Так как прямая перпендикулярна векторам и то в качестве направляющего вектора прямой можно взять их векторное произведение. Таким образом,