Занятие 6. Аналитическая геометрия на плоскости. Введение. Понятие уравнения линии

Предположим, что на плоскости задана декартова прямоугольная система координат и некоторая линия .

Рассмотрим уравнение

, (1)

связывающее две переменные и .

Определение 1. Уравнение (1) называется уравнением линии относительно заданной системы координат, если уравнению (1) удовлетворяют координаты и любой точки, лежащей на линии , и не удовлетворяют координаты и ни одной точки, не лежащей на линии .

Согласно этому определению сама линия представляет собой геометрическое место точек, координаты которых удовлетворяют уравнению (1)

Если в заданной системе координат уравнение (1) является уравнением линии , будем говорить, что (1) определяет линию .

Пример 1. Пусть декартова система координат. Требуется показать, что уравнение

(2)

является уравнением окружности радиуса с центром в точке .

Окружность по определению есть геометрическое место точек (совокупность тех и только тех точек), для каждой из которых расстояние до некоторой фиксированной точки есть величина постоянная.

Пусть – окружность радиуса с центром в точке .

(рис.1), или , или , или

– уравнение (2) в соответствии с определением 1 действительно определяет окружность .

Определение 2. Линия называется алгебраической, если в некоторой декартовой системе координат она определяется уравнением (1), в котором – алгебраический полином (т.е. сумма конечного числа слагаемых вида , – целые, – некоторая постоянная).

Если при этом – алгебраический полином порядка , линия называется линией порядка .

Например, окружность – алгебраическая линия второго порядка (см. пример 1).

Определение 3. Всякая неалгебраическая линия называется трансцендентной.

Пример 2. Уравнение представляет собой трансцендентную кривую. Эту кривую описывает точка подвижной окружности, которая касается изнутри неподвижной окружности вчетверо большего радиуса и катится по ней без скольжения. Эта кривая называется астроидой.

– параметрическое уравнение астроиды, см. Рис.2., астроида – синяя линия.

Рис. 2.

В Википедии наберите «астроида» или пройдите по ссылке http://ru.wikipedia.org/wiki/%D0%90%D1%81%D1%82%D1%80%D0%BE%D0%B8%D0%B4%D0%B0 и увидите, как получается эта линия в результате движения подвижной окружности, которая касается изнутри неподвижной окружности вчетверо большего радиуса.

Если интересно как был построен Рис.2., смотрите ниже огромную программу, желтым помечены главные моменты, все остальное – украшение.

t=0:pi/30:2*pi; a=1;

x=a*cos(t).^3; y=a*sin(t).^3;

% построение плоскости

axes('Box','on',...

'DataAspectRatioMOde','manual',...

'DataAspectRatio',[1 1 1],...

'FontAngle','italic',...

'FontName','Times',...

'FontSize',9,...

'FontWeight','bold',...

'NextPlot','add',...

'XAxisLocation','bottom',...

'XColor',[0.5 0 0],...

'XGrid','on','XDir','reverse',...

'XLimMode','manual',...

'XLim',[-1 1],...

'XTickMode','manual',...

'XTick',[-1,-.75,-.5,-.25,0,...

0.25,0.5,0.75,1],...

'XTickLabelMode','manual',...

'XTickLabel',...

'-1||-0.5||0||0.5||1',...

'YAxisLocation','right',...

'YColor',[0.5 0 0],...

'YGrid','on','YDir','normal',...

'YLimMode','manual',...

'YLim',[-1 1],...

'YTickMode','manual',...

'YTick',[-1,-.75,-.5,-.25,0,...

.25,.5,.75,1],...

'YTickLabelMode','manual',...

'YTickLabel',...

'-1||-0.5||0||0.5||1',...

'TickDirMode','manual',...

'TickDir','out');

% обозначение оси х

text('Color', [0.5 0 0],...

'FontAngle','italic',...

'FontName','Times',...

'FontSize',12,...

'FontWeight','bold',...

'HorizontalAlignment','center',...

'Interpreter','tex',...

'Position', [0 -1.18],...

'String',...

'x=a\cdotcos^3(t), t=[0..2\pi]',...

'VerticalAlignment','middle');

% обозначение оси у

text('Color', [0.5,0,0],...

'FontAngle','italic',...

'FontName','Times',...

'FontSize',12,...

'FontWeight','bold',...

'HorizontalAlignment','center',...

'Interpreter','tex',...

'Position',[-1.2 0],...

'Rotation',90,...

'String',...

'y=a\cdotsin^3(t), t=[0..2\pi]',...

'VerticalAlignment','middle')

% построение неподвижной окружности

rectangle('Curvature', [1 1],...

'LineWidth', 1.5,...

'Position', [-1 -1 2 2])

% построение подвижной окружности

rectangle('Curvature', [1 1],...

'EdgeColor', [1 0 0],...

'FaceColor', [0.8 0.8 0.8],...

'LineWidth', 1.5,...

'Position', [-0.78,0.28,0.5,0.5])

% построение графика

line(...

'Color',[0 0 1],...

'LineWidth',2.5,...

'LineStyle', '-',...

'XData',x,...

'YData',y)

hold on

line([-1,0;1,0],[0,1;0,-1],'Color','black')

Если набрать только желтые части программы, получим более простую картинку.

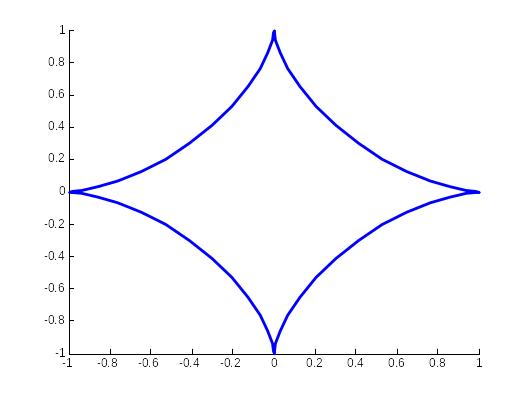
Рис. 3.

Раньше, используя функцию plot(x,y, ' '), мы строили только одну точку, сразу придавая аргументам x и y соответствующие координаты точки. С помощью этой функции можно строить не только одну точку, можно строить любые функции. Пусть нам дана некая функция Если аргумент x в функции plot( ) задать числовым массивом, суть которого значения абсциссы точек графика функции, а аргументу присвоить выражение-функцию зависящую от x, то мы будем иметь конечное число пар точек (x,y) – узлов. Узловые точки функция plot( ) соединяет прямыми линиями, а график функции выглядит кусочно-линейным. Чем больше будет узловых точек, тем больше график будет похож на настоящий график функции. Узловые точки с помощью маркеров в функции plot можно отметить особо.

Пример 3. Сравните графики двух парабол и , на промежутке , но с разным шагом:

>> x=[-5:5]; % задаем интервал для аргумента x с шагом 1

>> size(x) % наберите эту строчку, чтобы узнать размерность массива х,

% вы увидете, что это массив 1 х 11, то есть число узлов будет 11

>> y=x.^2; % задаем функцию

>> plot(x,y, '-o') % выводим график, узловые точки (здесь их 11) пометим круговыми маркерами,

% обратите внимание на прямолинейные соединения между узловыми точками

>> hold on

>> x=[-5:0.01:5]; % задаем интервал для аргумента x с шагом 1

>> size(x) % снова посмотрите размерность массива х,

% вы увидете, что это массив 1 х 1001, то есть число узлов будет 1001

>> y=x.^2-5; % задаем функцию

>> plot(x,y) % выводим график, узловые точки (здесь их 1001) маркерами помечать не будем,

% обратите внимание: узловых точек стало почти в 100 раз (в 91 раз) больше,

% поэтому график выглядит более гладко.

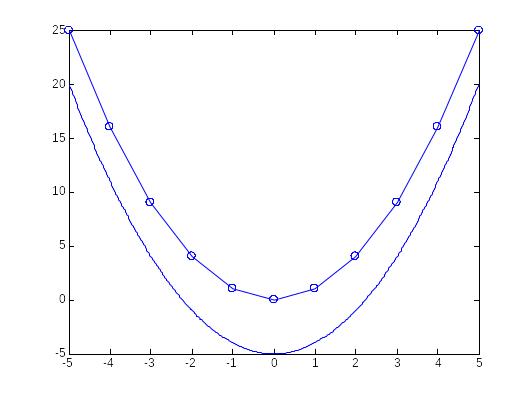
Рис. 4.

Для дальнейших упражнений снова понадобится таблица обозначений цветов и типов линий и маркеров:

Таблица 1 Таблица обозначений цветов и типов линий и маркеров
Цвет линии и маркера [код цвета в палитре RGB]			Тип маркера		Тип линии
b	синий (blue)	[001]	.	точка	- сплошная
g	зеленый (green)	[010]	o	круг	: пунктирная
r	красный (red)	[100]	x		-. штрих-пунктирная
c	голубой (cyan)	[011]	+	плюс	-- штриховая
m	фиолетовый (magenta)	[101]	*	звезда
y	желтый (yellow)	[110]	s	квадрат (square)
k	черный (black)	[000]	d	ромб (diamond)
w	белый (white)	[111]	p	пятиконечная звезда (pentagram)
			h	шестиконечная звезда (hexagram)
			^,<,>,v	треугольники