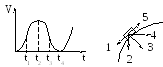Примеры тестовых заданий по физике

(с решениями)

Для специальностей биология, экология, химия дававшихся в 2007-2008 г

Содержание

1. МЕХАНИКА 2

2. МОЛЕКУЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА 9

3. ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ 13

4. КОЛЕБАНИЯ И ВОЛНЫ 24

5. ВОЛНОВАЯ И КВАНТОВАЯОПТИКА 27

6. КВАНТОВАЯ ФИЗИКА И ФИЗИКА АТОМА. ЭЛЕМЕНТЫ ЯДЕРНОЙ ФИЗИКИ И ФИЗИКИ ЭЛЕМЕНТАРНЫХ ЧАСТИЦ 34

Механика

1	Кинематика точки поступательного движения твердого тела
2	Динамика точки и поступательного движения твердого тела
3	Динамические параметры вращательного движения твердого тела
4	Динамика вращательного движения
5	Законы сохранения в механике
6	Элементы специальной теории относительности

 Закон движения материальной точки: х = 3t+ 4t².

Ускорение точки равно …

Уравнение равноускоренного движения тела по оси х имеет вид: х = х₀+V₀t+(at²)/2, где х₀– начальная координата,V₀– начальная скорость тела,a– его ускорение. Приведя уравнение условия задачи к данному виду находим, что а = 8.

Или исходя из определений: V=dx/dt,a=dV/dt=d²x/dt², взяв вторую производную получим:V= 3 + 8t,a= 8.

 Закон движения материальной точки по окружности (или вдоль оси х):

 = 4t³+3t(или х = 4t³+ 3t).

Угловое ускорение - (или ускорение - а) через 3 секунды составит …

Согласно определениям =d/dt(- угловая скорость),=d/dt, откуда, взяв вторую производную получим:

 = 12t²+ 3,= 24t, то есть через 3 секунды это будет 72 рад/с².

Аналогично для линейного движения: a=dV/dt,V=dx/dtили

V= 12t²+ 3,a= 24t, то есть через 3 секунды это будет 72 м/с².

Материальная точка М движется по окружности со скоростьюV. На первом рисунке показан график зависимости проекции скоростиV_(- единичный вектор положительного направления,V_- проекцияV на это направление). При этом вектор полного ускорения на втором рисунке имеет направление …

Ускорение при криволинейном движении можно записать а=а_+а_n= (dV/dt)+ (V²/R)n.

Первое слагаемое – тангенциальное ускорение – направлено по касательной к траектории. Поскольку (dV/dt) отрицательно, то оно направлено в сторону 1. Второе слагаемое – нормальное (центростремительное) ускорение при движении по окружности всегда направлено к центру окружности, по которой происходит движение (направление 3).

Результирующее ускорение 1 + 3будет направлено в сторону4.

Если скорость постоянна, будет направление 3, если скорость растет – 2. Направление 1 (1) возможно только при движении по прямой.

 Точка М движется по окружности с постоянным тангенциальным ускорением. Если проекция тангенциального ускорения на направление скорости отрицательна, то величина нормального ускорения …

1) не изменяется 2) уменьшается 3) увеличивается

Если тангенциальное ускорение отрицательно, то модуль скорости уменьшается. Поскольку а_n=V²/R, нормальное ускорение по модулю будетуменьшаться.

В случае положительного значения проекции тангенциального ускорения на направления скорости – скорость по модулю будет возрастать и, следовательно, нормальное ускорение тоже будет увеличиваться.

 Точка М движется по спирали с постоянной по величине скоростью. При этом величина нормального ускорения …

1) не изменяется 2)увеличивается 3) уменьшается

Поскольку а_n=V²/R, нормальное ускорение при постоянном модуле скорости будетуменьшатьсяпри увеличении радиуса (удаление от центра спирали) илиувеличиваетсяпри движении к центру.

 Если а_и а_n – тангенциальная и нормальная составляющие ускорения, то для равномерного движения по окружности справедливы соотношения:

1) а_=а=const, а_n= 0; 2)а_= 0, а_n=const;

3) а_= 0, а_n= 0;4)а_= 0, а_n0

При равномерном движении по окружности модуль скорости не меняется, значит (см. формулу предыдущего теста) а_= 0. Нормальное ускорение отсутствует при равномерном движении по прямой, при равномерном движении по окружности а_n=const=V²/R(модуль), но направление меняется. Значит правильно соотношение4): а_= 0, а_n0.

 Величина скорости автомобиля изменялась во времени, как показано на графике V(t). В момент времениt₂(t₁,t₃,t₄) автомобиль поднимался по участку дуги.

Направление результирующей всех сил, действующих на автомобиль в этот момент времени правильно отображает вектор 1, 2, 3, 4 или 5?

Согласно второму закону Ньютона F=ma, гдеF– результирующая сила, действующее на тело,а– его ускорение. То есть направление результирующей силыFсовпадает по направлению с ускорениема.

В момент времени t₂скорость автомобиля не менялась, при этом тангенциальное ускорение а_=0. При движении по дуге на тело действует центростремительное (нормальное) ускорение, направленное к центру окружности, касательной к дуге в этой точке (направление 3)

В момент времени t₁скорость возрастала, то есть а_>0, направлено по направлению 5, а_n– к центру (направление 3). Суммарное ускорение3+5направлено по4.

В момент времени t₃скорость уменьшалась, то есть а_<0, направлено по направлению 1. Суммарное ускорение1+3направлено по2.

Момент времени t₄аналогичен моменту времениt₂: а_=0, ноV= 0, и, следовательно а_n.= 0.

 Диск вращается равноускоренно вокруг горизонтальной оси. Укажите направление:

1) вектора угловой скорости точки А на ободе диска.

2) вектора тангенциального ускорения точки А на ободе диска.

3) вектора углового ускорения точки А на ободе диска.

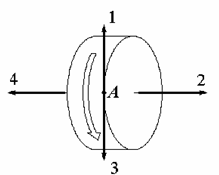
В механике угловой скоростью является вектор (псевдовектор), направленный по оси вращения в сторону, определяемую правилом «буравчика», в данном случае направление 2. Угловая скорость для всех точек вращающегося тела одинакова.

Тангенциальное ускорение точки направлено по касательной к траектории, то есть в направлении 3 при ускоренном движении или 1 при замедленном.

Угловое ускорение – производная от угловой скорости. Направлено по оси вращения, как и угловая скорость 2 при ускоренном движении или 4 при замедленном.

 К точке, лежащей на внешней поверхности диска, приложены 4 силы. Если ось вращения проходит через центр О диска перпендикулярно плоскости рисунка, то плечи сил F1, F2, F3, F4, будут a, b, c, или 0.

Плечо силы относительно оси вращения проходящей через центр диска это расстояние от оси вращения до прямой, проходящей через вектор силы.

Для сил: F₁–c,F₂– а,F₃– 0,F₄–b.

 Тело массой 2 кг поднято над Землей. Его потенциальная энергия 400 Дж. Если на поверхности Земли потенциальная энергия тела равна нулю и силами сопротивления воздуха можно пренебречь, скорость тела после прохождения ¼ расстояния до Земли составит: 10, 14, 20, 40 м/с

Закон сохранения энергии Е_К+ Е_П= (mV²)/2 +mgh=const= 400 Дж.

Для максимальной высоты подъема Hзапишем:

mgH= 400 Дж.

Для высоты (3/4)Н (после прохождения ¼ расстояния до Земли):

(3mgH)/4 + (mV²)/2 = 400 Дж.

Если учесть, что (3mgH)/4 = (4003)/4 Дж = 300 Дж, то есть в предыдущем уравнении (mV²)/2 = 100 Дж. При весе тела 2 кг,V²= 200/2 (м/с)².V= 10 м/с.

На рисунке показан вектор силы, действующей на частицу. Работа, совершенная этой силой при перемещении частицы из начала координат в точку с координатами (5;0), равна …

1) 2 Дж 2) 15 Дж 3) 10Дж

Работа это скалярное произведение

силы на перемещение:

А = Fs=Fscos= 4 (Н) 5 (м)cos60= 10 Дж

 Система состоит из трех тел с массами m₁= 1 кг,m₂= 2 кг,m₃= 3 кг, которые двигаются, как показано на рисунке

Если скорости шаров V₁= 3 м/с,V₂= 2 м/с,V₃= 1 м/с, то величина скорости центра масс этой системы равна …м/с 10, 2/3, 5/3, 4.

Скорость центра масс определяется равнением:

V_Ц= (m₁V₁+m₂V₂+m₃V₃)/(m₁+m₂+m₃)

Следует сразу обратить внимание, что m₁V₁+m₃V₃= 0 и центр масс будет двигаться в направленииXсо скоростью

V_Ц= (m₂V₂)/(m₁+m₂+m₃) = 4/6 м/с = 2/3 м/с.

В потенциальном поле силаFпропорциональна – градиенту потенциальной энергии Е_П. Если график зависимости потенциальной энергии Е_Пот координаты Х имеет вид, то зависимость проекции силыF_Хна ось Х будет …

Связь проекции силы F_Хс потенциальной энергией запишется:

F_Х= – (dE_П/dх).

Если предположить, что E_П= ах², тоdE_П/dх = ах, учитывая знак «–» выбираемответ 3.

 Тонкостенная трубка и диск имеют одинаковые массы и радиусы Для их моментов инерции справедливо соотношение…

1) I_т<I_д2) I_т > I_д3)I_т=I_д

Момент инерции тела относительно оси вращения равен

I=m_ir_i²,

где m_i– масса элемента тела,r_i – расстояние этого элемента до оси вращения.

Очевидно, что любое полое тело будет иметь больший момент инерции, поскольку его масса удалении от оси. Момент инерции трубки будет больше, чем диска.

 Диск и цилиндр имеют одинаковые массы и радиусы. Для их моментов инерции справедливо соотношение:

1) I_ц<I_д2)I_ц>I_д3) I_ц = I_д

(Другой вариант: кольцо и тонкостенная трубка имеют одинаковые массы и радиусы Для их моментов инерции справедливо соотношение…

1) I_т<I_к2)I_т>I_к3) I_т = I_к

R, m, I₁

С точки зрения динамики вращательного движения относительно оси симметрии тел между телами разницы нет, поэтому I_ц = I_д = (mR²)2.

(Другой вариант: I_т = I_к = mR²)

 Из жести вырезаны три одинаковые детали в виде эллипса. Две детали разрезали пополам вдоль разных осей симметрии. Затем все части отодвинули друг от друга на равное расстояние и расставили симметрично оси ОО.

Для моментов инерции получившихся фигур относительно оси ООсправедливо соотношение …

1) I1 = I2 > I3 2) I1 > I2 > I3 3) I1 < I2 = I3 4) I1 < I2 < I3

Момент инерции тела определяется как I=m_ir_i², гдеm_i– масса элемента, r_i– его расстояние до оси вращения. С этой точки зрения тела 1 и 2 не отличаются друг от друга, то естьI₁=I₂. Для третьего тела его элементы находятся ближе к оси вращения, значит его момент инерции меньше, и окончательноI₁=I₂>I₃.Правильно соотношение 1).

 Сплошной и полый цилиндр имеют одинаковые радиусы и массы. Какой из них выше закатится без проскальзывания по наклонной плоскости, если начальные скорости их одинаковы?

1) Выше поднимется сплошной цилиндр