подгон 2018 (легендарный) / 1 семестр / Линейная алгебра / Коллоквиум 1 поток / Новая папка / 25 Приведение к каноническому виду уравнения кривой 2-го порядка. Классификация кривых 2-го порядка

Общее уравнение:

Преобразуем уравнение переносом начала системы координат в центр поверхности и поворотом системы для получения уравнения вида:

Для удобства запишем:

а)случай

При всех положительных лямбдах и a преобразованиями мы получаем уравнение эллипсоида:

При получаем уравнение однополостного гиперболоида:

При можем записать уравнение двуполостного гиперболоида:

При a=0 получаем поверхность второго порядка, называемую конической, при том каноническое уравнение конической поверхности предполагает :

б)

Все лямбды положительны, получаем уравнение эллиптического цилиндра:

В случае, если лямбды имеют различные виды, то уравнение не сложно привести к виду уравнения гиперболического цилиндра:

в)

Зададим уравнение заменой коэффициента a на координату z:

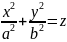
Рассмотрим два случая:

X=0, парабола, являющаяся сечением эллиптического параболоида плоскостью x=0:

Y=0, парабола, являющаяся сечением эллиптического параболоида плоскостью y=0:

Отдельный случай.

Рассмотрим отдельную поверхность. Седловая поверхность. Параболический гиперболоид.