подгон 2018 (легендарный) / 1 семестр / Линейная алгебра / Коллоквиум 1 поток / Новая папка / 11Уравнение плоскости

Общее уравнение плоскости

Общее уравнение плоскости имеет вид  , где коэффициенты   одновременно не равны нулю.

Уравнение плоскости по точке и двум неколлинеарным векторам

Рассмотрим точку   и два неколлинеарных вектора  .Уравнение плоскости, которая проходит через точку   параллельно векторам  ,выражается формулой:

! Примечание: под выражением «вектор параллелен плоскости» подразумевается, что вектор можно отложить и в самой плоскости.

Принципиально ситуация выглядит так: 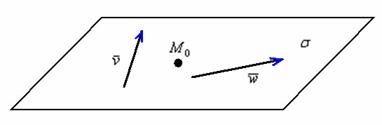Обратите внимание, что точка и два коллинеарных вектора не определят плоскость (векторы будут свободно «вертеться» вокруг точки).

Уравнение плоскости по трём точкам

Любые ли три точки пространства задают плоскость? Нет. Во-первых, точки должны быть различными. А во-вторых, они не должны лежать на одной прямой (сразу все три).

Уравнение плоскости, проходящей через три различные точки  , которые не лежат на одной прямой, можно составить по формуле:

На самом деле это разновидность предыдущего способа, смотрим на картинку: 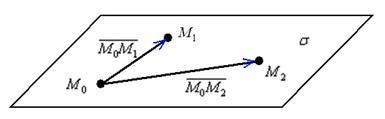Если известны три различные точки, не лежащие на одной прямой, то легко найти два неколлинеарных вектора, параллельных данной плоскости:

Вектор нормали плоскости (нормальный вектор)

Вектор нормали плоскости – это вектор, который перпендикулярен данной плоскости. Очевидно, что у любой плоскости бесконечно много нормальных векторов. Но для решения задач нам будет хватать и одного. Если плоскость задана общим уравнением  , то вектор    является вектором нормали данной плоскости. Всё, что нужно сделать – это «снять» коэффициенты из уравнения плоскости.

Уравнение плоскости по точке и вектору нормали

Выберем произвольную точку пространства. Очевидно, что через данную точку можно провести единственную плоскость, перпендикулярную вектору нормали.

Уравнение плоскости, проходящей через точку   перпендикулярно вектору   , выражается формулой:

В некоторых задачах аналитической геометрии уравнение плоскости можно составить несколькими способами, и решение через точку и нормальный вектор – самое оптимальное.