
Эталон_Курсовая_МТУСИ_Электродинамика_ЭИРР_Автор Гаврилов.docx
.docxМИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования
МОСКОВСКИЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ СВЯЗИ И
ИНФОРМАТИКИ
Курсовая работа По дисциплине:
«ЭиРР»
По теме:
«Анализ электромагнитного поля в диэлектрическом волноводе»
Выполнил
студент группы
БРА 1901
Гаврилов Егор
Москва 2021
Содержание
1. Техническое задание…………………………………………………………...3
2. Определение комплексных амплитуд
всех остальных проекций у векторов
 и
и
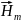 в средах 1 и 2 при
в средах 1 и 2 при
 ………………………………………………..4
………………………………………………..4
3. Составляются и совместно решаются
уравнения, которые связывают между
собой неизвестные поперечные волновые
числа в средах 1 и 2, т.е.
 и
и
 …………………………………………………………………………………...6
…………………………………………………………………………………...6
4. Определяются минимальная и максимальная толщины световода, при которых по нему будет распространятся только волна низшего типа………...8
5. Для средней толщины световода
вычисляются параметры для волны низшего
типа, т.е.
,
,
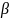 и
и
 …………………………………………………9
…………………………………………………9
6. Используя заданную величину единичной
мощности волны либо в среде 1, либо в
среде 2, т.е.
 или
или
 ,
определяются амплитуды А и В, входящие
в выражение для всех проекций векторов
и
…………………………….10
,
определяются амплитуды А и В, входящие
в выражение для всех проекций векторов
и
…………………………….10
7. Строятся зависимости амплитуд всех
проекций векторов
и
от координаты x в области
и в области
 ……………………………..11
……………………………..11
8. Вывод…………………………………………………………………………..13
1. Техническое задание
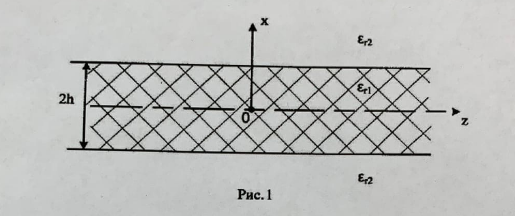
Определить структуру гармонического электромагнитного поля в плоском диэлектрическом волноводе ( световоде), изображенном на рис.1. Известны комплексные амплитуды двух проекций векторов поля в среде 1 и 2 при ( таблица 1). Параметры световода приведены в таблице 2. Потери в диэлектриках отсутствуют.
 Таблица
1.
Таблица
1.
Номер варианта по журналу группы |
Известные проекции векторов
|
Известные проекции векторов и в среде 2 |
Дополнительные сведения |
9 |
|
|
|
Таблица 2.
Номер варианта по журналу группы |
|
|
|
, мВт |
, мВт |
9 |
2.6 |
1.3 |
1.3 |
1 |
- |
2. Определение комплексных амплитуд всех остальных проекций у векторов и в средах 1 и 2 при . Дано:
![]()
![]()
![]()
![]()
![]()
Используем формулу связи:
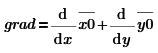
![]()
![]()
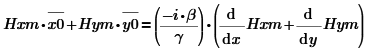
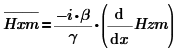

Найдем

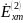



![]()
![]()
![]()
![]()
Используя уравнение Максвелла, найдем
комплексные амплитуды проекции у
векторов
.
 m=
- iωμ
,
следовательно
m=
- iωμ
,
следовательно
![]()
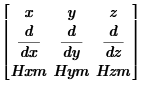
![]()
![]()
![]()
![]()
![]()
Из
этого выражения следует, что
 и
и
 Найдем
Найдем
 и
и
 :
:
![]()
![]()
![]()
![]()
![]()
![]()
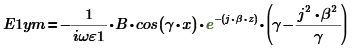

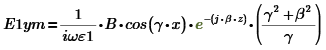

![]()
![]()
![]()
![]()
![]()
![]()



![]()
![]()
3. Составляются и совместно решаются
уравнения, которые связывают между
собой неизвестные поперечные волновые
числа в средах 1 и 2, т.е.
и
Составим
первую систему уравнений:

![]()
![]()
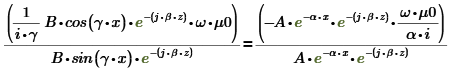

![]()
![]()


![]()
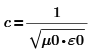
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Совместно составим 2 уравнения.
Произведем
нормировку двух уравнений, для этого
домножим обе части на
 и на
и на

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

4. Определяются минимальная и
максимальная толщины световода, при
которых по нему будет распространятся
только волна низшего типа.
Для
того, чтобы определить минимальные и
максимальные толщины световода, при
которых по нему будет распространятся
только волна низшего типа нужно изобразить
график, на котором распространяется
только волна низшего типа:
Т.к. у
нас котангенс
 и
и
 будут такими:
Определим минимальную
и максимальную толщины световода:
будут такими:
Определим минимальную
и максимальную толщины световода:
![]()
![]()
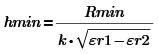
![]()

![]()
5. Для средней толщины световода вычисляются параметры для волны низшего типа, т.е. , , и .
![]()
![]()
![]()
Найдем
на графике пересечение:
 Получаем,
что
Получаем,
что


![]()

![]()

Найдем :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Найдем :

![]()
Проведем проверку:
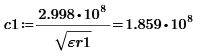

![]()
![]()
6. Используя заданную величину единичной
мощности волны либо в среде 1, либо в
среде 2, т.е.
или
,
определяются амплитуды А и В, входящие
в выражение для всех проекций векторов
и
.

Нам понадобится только z область, поэтому получаем формулу проекции Пойтинга на ось z:

![]()
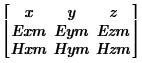
![]()
![]()
![]()
![]()
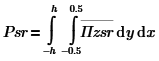

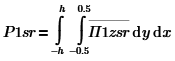

![]()
![]()
![]()
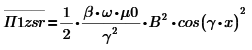
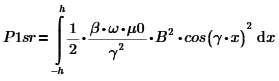
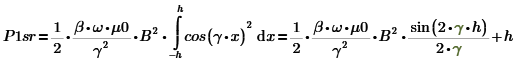
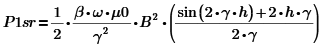
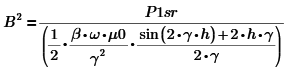
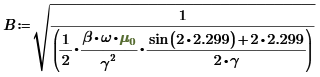

Найдем А:
![]()

все проекции векторов и :
![]()
![]()
6)Построить зависимости амплитуд всех проекций векторов от координаты х
Случаи: Еу Нх Нz.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

 и
и
 в среде 1
в среде 1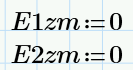


 ,
мкм
,
мкм