13. Рассчитаем и построим график зависимости коэффициента затухания волны в волноводе от частоты.

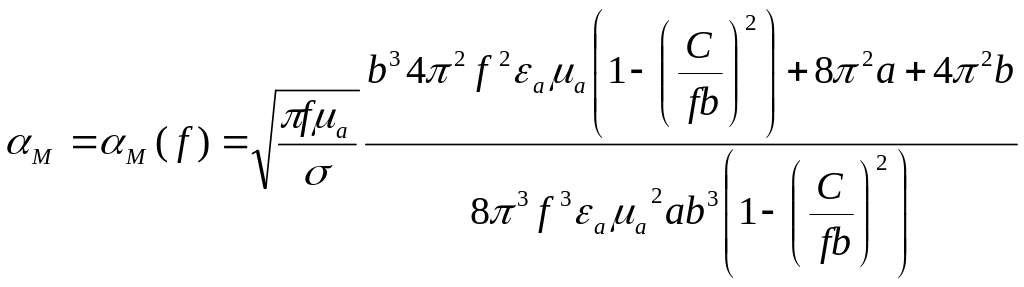
График этой зависимости, запрограммированной в пакете MathCad 14, представлен на рис. 15.

Из графика видно, что процесс действительно затухающий (с ростом частоты уменьшается коэффициент затухания). При приближении к критической частоте наблюдаются большие потери энергии, а при удалении от критической частоты мы видим резкое падение затухания.

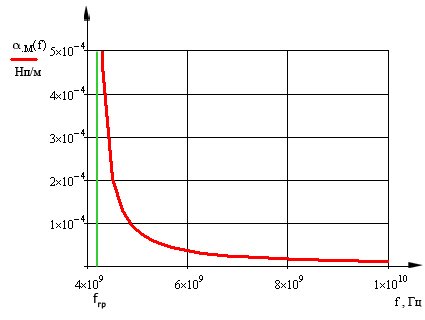
рис. 15

14. Определим тип волны, распространяющейся в волноводе. Изобразим структуру силовых линий электрического и магнитного полей этой волны и плотности поверхностного тока проводимости, протекающего по стенкам волновода.

У данной волны имеется составляющая, но нет составляющей, из чего следует, что это волна H-типа

Значения m и n можно определить из проекции на вектора H на ось z.

В нашем случае x составляющая отсутствует, поэтому m = 0. Коэффициента перед говорит о том, что n = 2. И, если подставить значения m = 0, n = 2 в формулу для расчета критической длины волны, получим:

см

Что совпадает с полученной ранее критической длиной волны.

Значит, рассматриваемая волна является волной типа .

Структура силовых линий электрического и магнитного полей волны в прямоугольном волноводе

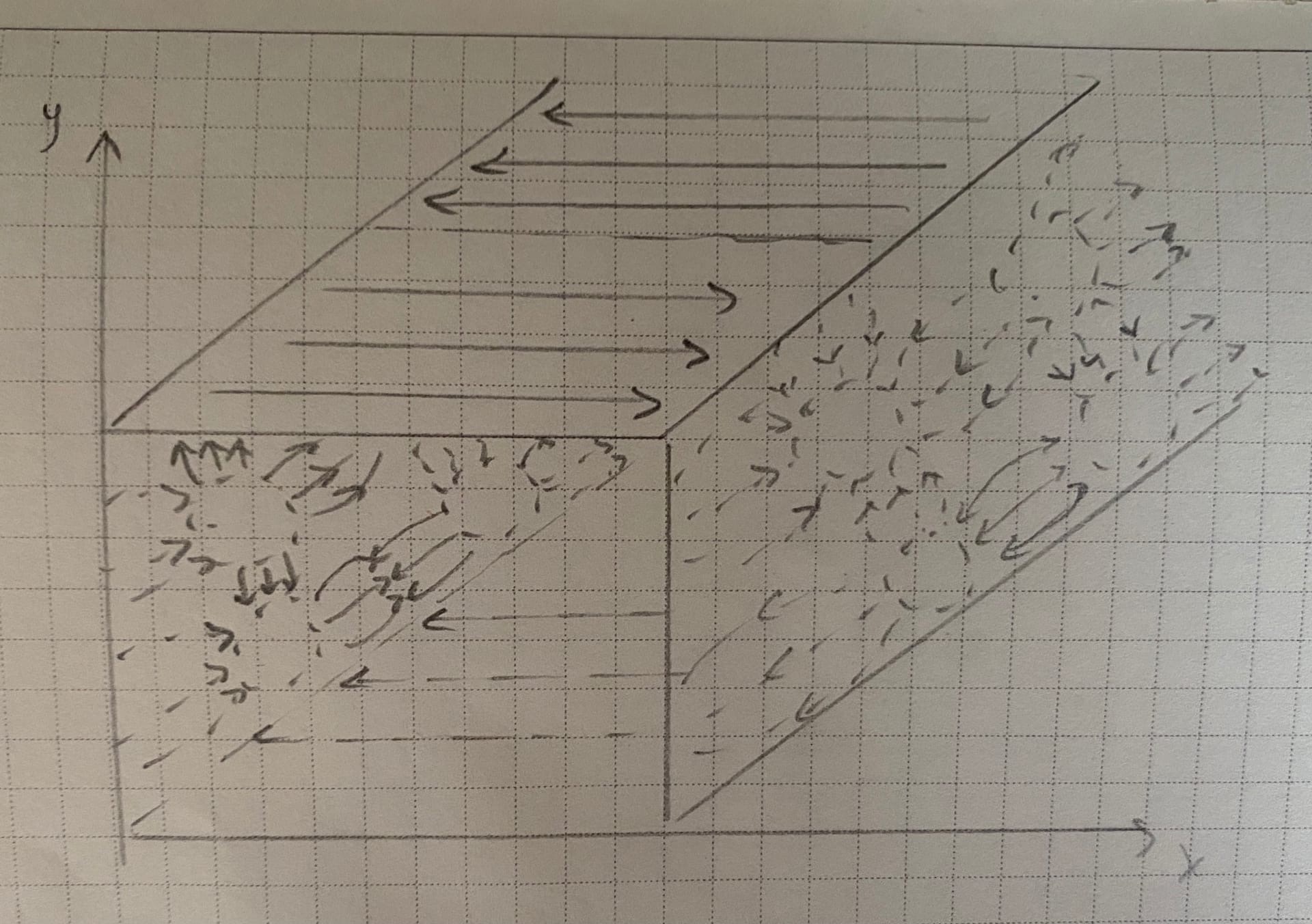
токи на стенках

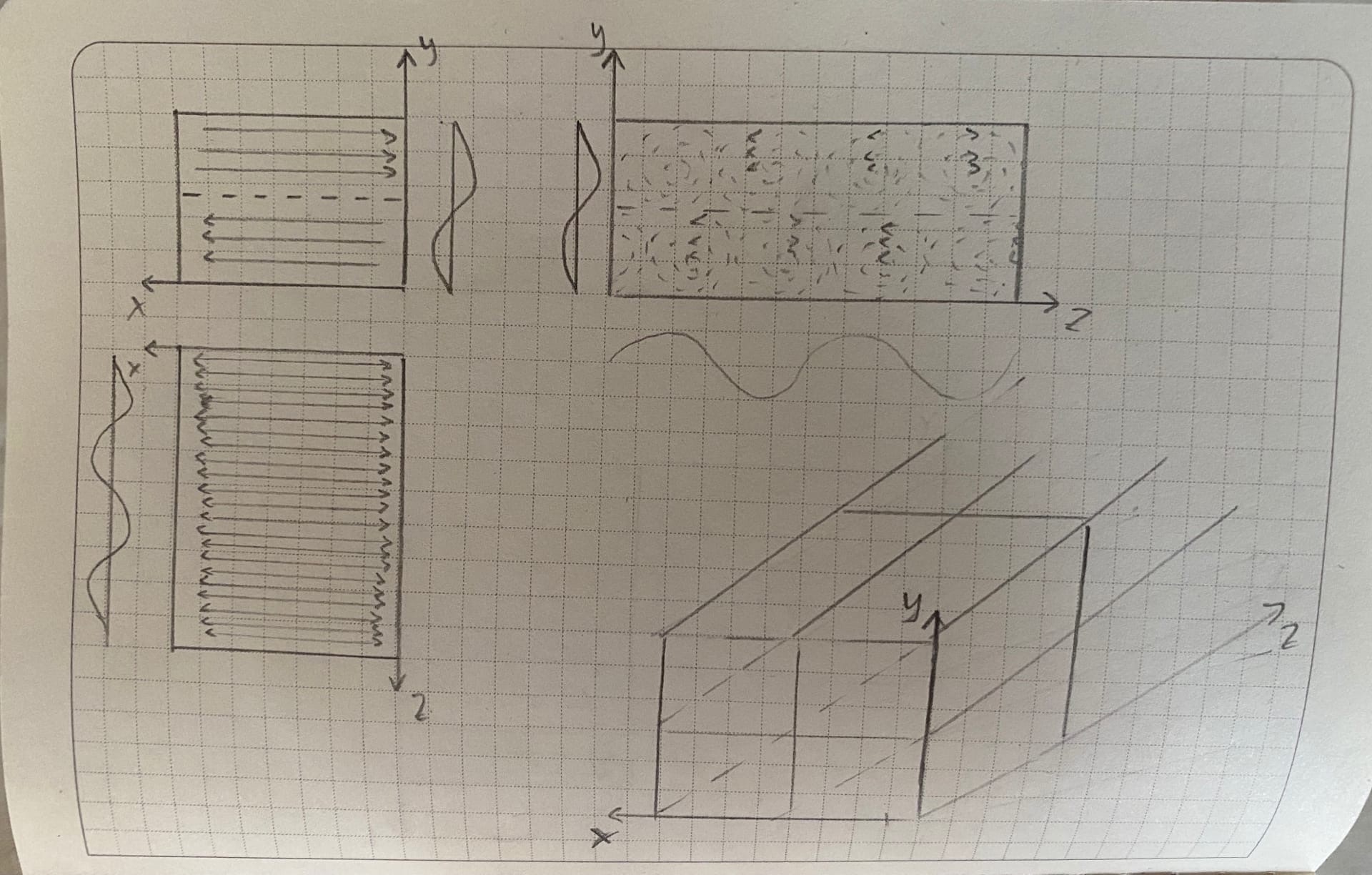
структура волны

15. Вывод.

Данная работа была посвящена теоретическому исследованию электромагнитного поля в прямоугольном волноводе. В ходе изучения данного поля с помощью известной комплексной амплитуды вектора напряжённости электрического поля мы смогли полностью описать поле, найдя все составляющие обоих его векторов. Была установлена критическая частота, дающая возможность судить о том, в каком диапазоне волна является бегущей. Построив графики зависимостей амплитуд от координат, мы пришли к заключению, что представленная волна относится к типу , так как зависимость от координаты x имеет линейный характер, а график зависимости от координаты y даёт понять, что на стенке укладывается одна полуволна. На примере верхней стенки волновода было проверено выполнение граничных условий для касательной составляющей вектора Е и нормальной составляющей вектора Н. Также были найдены комплексные амплитуды плотностей поверхностных токов и зарядов. Записав выражения для вектора Пойнтинга в предварительно найденных диапазонах бегущей и стоячей волны, мы убедились в правильности предыдущих вычислений: в предполагаемом режиме стоячей волны переносы энергии, в отличии от режима бегущей волны, не было. Мы определили фазовую скорость и скорость распространения энергии, а также графически построили их зависимости от частоты, для наглядности указав значение скорости света для данной среды. Использование граничных условий Леонтовича-Щукина помогло нам в определении коэффициента затухания для заданной волны. Его зависимость от частоты также была нанесена на график. Имея представление о волне на основании исследований, нам удалось изобразить структуру силовых линий электрического и магнитного полей и структуру силовых линий плотности поверхностного тока проводимости, протекающего по стенкам волновода. Наглядные подтверждения правильности полученных данных в виде графиков дают нам возможность говорить о том, что мы верно построили математическую модель поля.