1.3.3. Неэталонный индекс блочности. Математическая модель блочности

Невооруженным глазом заметно, что данное изображение имеет блочную структуру, т.е. содержит артефакты блочности. Поскольку артефакты блочности, возникающие в горизонтальных и вертикальных направлениях, ничем не отличаются друг от друга, предложенный алгоритм будет описан только для измерения горизонтальных артефактов блочности.

Каждый блок можно представить как сумму постоянной составляющей и независимого равномерно распределенного белого шума с нулевым математическим ожиданием и неизвестной дисперсией.

Рассмотрим два соседних блока 8 × 8 пикселей исо средними значениямиисоответственно, где. Таким образом, эти блоки можно описать следующими формулами [5]:

, , (6)

где и- слагаемые, являющиеся независимым равномерно распределенным белым шумом с нулевым математическим ожиданием. Когда коэффициенты ДКП соответствующих блоковиквантуются с большим шагом квантования, большинство квантованных коэффициентов равны нулю, что снижает переменные составляющиеи. В результате ступенчатая двумерная функция междуиможет стать видимой (из-за того, что), создавая артефакт блочности, как показано на рис. 1. Основываясь на этом наблюдении, мы формируем новый смещенный блок, составленный из правой половиныи левой половины, как показано на рис. 2.

Рис. 2. Иллюстрация формирования нового смещенного блока

Артефакт блочности между блоками иможет быть смоделирован как ступенчатая двумерная функция в блоке. Определим ступенчатый двумерный блокв новом смещенном блокекак [5]:

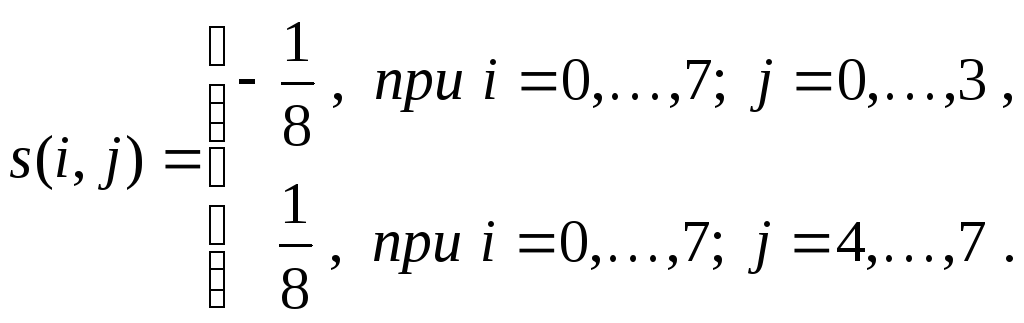(7)

Таким образом, смещенный блок можно представить в виде следующего выражения:

(8)

где– это амплитуда ступенчатой двумерной функции,– это среднее значение блока, показывающее локальную яркость фона, а– это остаточный блок, который описывает локальную детализацию на границе исходных блокови. Чем больше значение величины, тем больше артефакты блочности при неизменных яркости фона и локальной детализации. Далее применяется эффективный алгоритм на базе пространства ДКП, с помощью которого находятся коэффициенты ДКП блокаи величины параметров,и.

Представление модели блочности в пространстве дкп

Для перехода в область ДКП-коэффициентов определим две матрицы иследующим образом [5]:

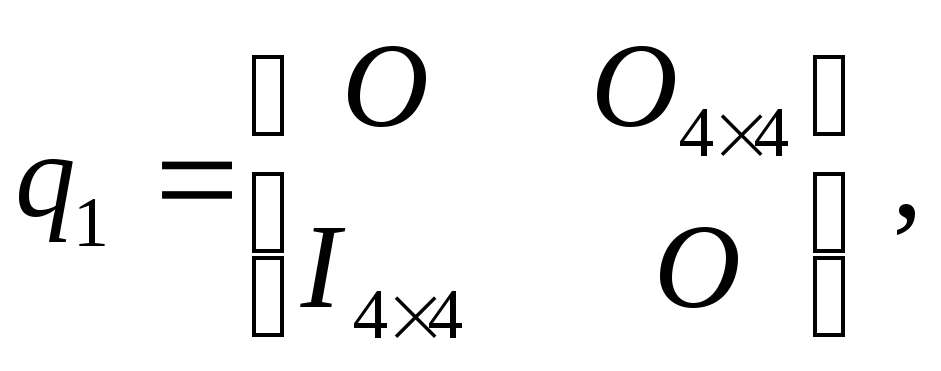
(9)

где – это тождественная (единичная) матрица, а– нулевая матрица. Представим смещенный блокв виде

(10)

Используя свойства линейности и дистрибутивности ДКП, легко получить отображение (9) в пространстве ДКП.

(11)

где ,,,и– это матрицы коэффициентов ДКП для блоков,,,исоответственно. Несмотря на то, что матрицыисодержат много нулей, соответствующие им в пространстве ДКП матрицыине разрежены. Это означает, что для полученияпотребуется совершить много операций умножения. Однако матрица суммыи матрица разностисодержат много нулей (более 50% от всех элементов), поэтому значительная экономия в вычислительных операциях может быть достигнута с помощью следующего уравнения:

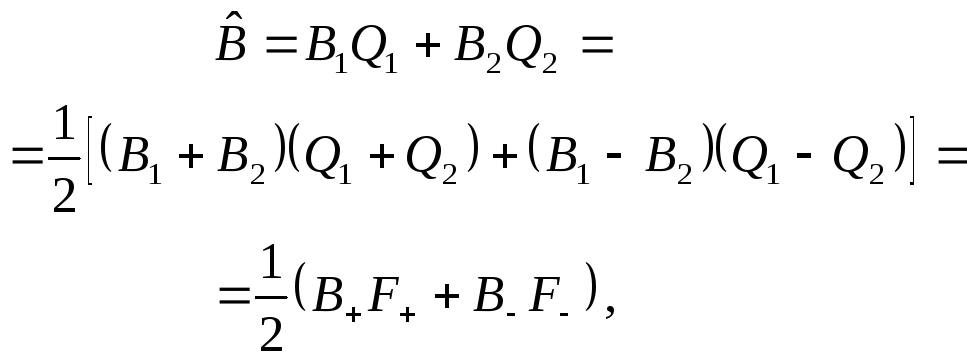(12)

где , а. Отметим, что ДКП ступенчатой двумерной функцииимеет лишь четыре ненулевых элемента в первой строке, поскольку– это матрица, постоянная в вертикальном направлении и антисимметричная в горизонтальном направлении. Пусть вектор– первая строка матрицы коэффициентов ДКП ступенчатой двумерной функции. Тогда. Из свойства унитарности ДКП получаем, что

(13)

Таким образом, параметры из (8) могут быть посчитаны по формулам:

(14)

(15)

Пусть – это матрица коэффициентов ДКП остаточного блока. Тогдаможно легко получить последовательным выполнением следующих логических операций:

(16)

Благодаря разреженности коэффициентов ДКП, предложенный алгоритм гораздо более эффективен, чем традиционные методы, такие как [6-11], даже если используются быстрые алгоритмы ДКП [12, 13-21].