TR_4_FNP

Добавил:

CyberTechWiz Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Липецкий государственный технический университет

Предмет:

Математический анализ

Файл:

2.13. z = ln

.pdf

Скачиваний:

Добавлен:

14.09.2024

Размер:

1.64 Mб

Скачать

☆

Задание 1. Найти частные производные первого порядка функции.

1.1.z= ln 2 (3x+2y).

1.2.z = x 2 у еху .

1.3.z = ln(3x 2 у4 ) е у .

1.4.z = е3 х2 5 у3 .

1.5.z = arcctg (xy 2 ).

1.6.z = (3x²- y+3) 4 .

1.7.z = sin 5х2 у3 .

1.8.z = x ln y xy2 .

1.9.z = ctg (3x – 2y) + y3 .

х2

1.10.z = х у2 .

1.11.z = ln 2 ( ху 1).

1.12. z =	х2	ln y2 x4 y .
	у

1.13. z = arctg x2 . y

1.15.z = sin x y .

1.16.z = sin (xy 3 ) .


	x
1.17. z = tg		.
1.17. z = tg	x y	.

1.18. z = ln (x + y²) - x . 1.19. z = ln (2 x - 3 x ). 1.20. z = x 2 e3 x 3 y .

1.21. z = arcctg x3 . y

1.22. z = sin ( e x y2 ).


	y
1.23. z = cos		.
1.23. z = cos	x y	.

1.24.z = ln (y² - e х ).

1.25.z = arcsin ху .

1.26.z = arcctg (x²+y²).

1.14. z = e x (cos y x sin y) .

Задание 2. Найти полные дифференциалы первого и второго порядков функции.

2.1.	z = cos (2x ln( xy)) .
2.2.	z = arcsin( 2x3 y) .
2.3.	z = ln 2 (4y x3 ) x3 y7 .

2.4.	z = cos(x		xy3 ) .
2.5.	z = y arctg		x	.

		y2

2.6. z = tg 2x y2 .

2.7.z = (5x2 x3 y y3x 7)4 .

2.8.z = e x3 y3 .

2.9.z = у ln x y x .

2.10.z = arcos (3x-y²).

2.11.z = cos² (xy).

2.12. z = sin	х у		.

	х2 у	2

2.14.z = ln( x3 y3 ) 3 xy .

2.15.z = sin 2 (3х 4 у) .

		у
2.16. z =		у		х е у .

	3х	5 у
	3х	5 у

2.17. z = е х2 у2			х2		.
2.17. z = е х2 у2					.
			у

2.18.z = 2 х2 у2 sin( xy) .

2.19.z = arccos y2 .

2.20.z = ctgx2 y yx .

2.21.z = cos 3x2 2y3 x4 y5 .

2.22.z = ln( 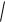x2 y3 3) .

2.23.z = tg(x3 y4 ) ex y .

z =

2.24.

2.26.

z =

cos

x2 y

x y

2.25. z = 23x2 у5

ln( x4 y3 ) .

Задание 3. Найти производную функции у = у(х), заданной неявно.

3.1. y= ехсоsy ey sin x .

3.15.

arctg

x2 y2 .

3.2. y -2y-sinx = 0.

3.16.

3.3. xy + ln (xy) =1.

3.17. sin (х у) (х

ху у) .

3.4. e аrctg( x y)

x .

3.18.

sin x

sin( xy) .

x y

3.5.

x y

3.19. (x²+y²-x)² =x²+y².

3.6. x²-1+cos (xy) =0

3.7. ex y x y

3.20. (y-x²)² = x 5 .

3.8. y =ln tg

3.21.

y sin x + x² +y³=1.

3.9. x²y+x sin y 0 .

3.22. xy = y х .

3.10.

x cos(πy)-y sin (πx) =x-1.

3.23. xy + ln (x+2y) = 5.

3.11.

(y-x)³+x+6 =0.

3.24. x²-1+sin (x3 +y) =0

3.12.

y х2 х

3.25.

уех е у х 0 .

3.13.

ln (x³+2y³) =

ху .

3.26.

arctg(2x y) e x 0 .

3.14.

sin y ex xy2

Задание 4. Найти производную сложной функции

Найти производную	dz	сложной функции z = z (x,y), если х = х (t); y = y (t).
	dt

4.1. z = 2−3 ;			х = sin t;	y = t³.
4.2. z = ln (e х
			y) ; x = t 2 ;	y = t .
					t
4.3.	z = y x ; x =ln (t-1) ; y = e 2 .
4.4.	z = e у 2 х 7 ;	x = sin 3t;		y = cos 5t.

4.5.	z = x 3 e 2 у ;				x =	1	;	y= ln t.
4.5.	z = x 3 e 2 у ;				x =		;	y= ln t.
						t
4.6.	z =	arcsin		x	; x=2-e 3t ;			y = arctg t.
4.6.	z =	arcsin		y	; x=2-e 3t ;			y = arctg t.
				y
		х2						y =t 3 .
4.7. z =			;		x=1-3t² ;
4.7. z =			;		x=1-3t² ;
		у 1

4.8. z = ln(e х е 2 у );

x=e t ; y =cos t

2 .

4.10.

z =

;

x=sin 2t;

y =tg t.

4.9.

z = arctg (xy); x =t-10;

y = e 5t .

Найти частные производные

сложной функции z=z(x,y),

если

x=x(u,v);

y=y(u,v).

4.11.

z arctg(x y) ;

x u2 ;

y u3 .

4.17. z arccos

y 2

; x sin( u )

4.12. z

x y 1 ;

x cos(u )

; y

u .

y cos(u ) .

4.13.

z ln( e

3 y

) ;

x u

;

y e

2u 3

4.18.

;

x 2u ;

2 y

2 1

4.14.

z arcsin

;

4.19.

z x3e y

;

x 2 u

2 ;

y ln

4.15.

x y2

5 ; x ln

y eu .

4.20.

z tg(3x 5y) ; x u cos ;

y sin u .

y 3u

4.16.

z y ;

;

2 2

Найти производную

сложной функции z z(t, x, y) , если x x(t) ;

y y(t) .

4.24.

;

x sin t ;

y cos t .

4.21. z 53t y 2 x ;

x 3 t ;

t x

2t 1

t 2

z ctg

4.25.

t3 x2

y ; x

;

4.22.

;

t .

4.23. z cos(x2

2 ) ;

x 2t 3 ; y 5t 2 .

z y

2 x t

4.26.

;

3t 1; y

Задание 5. Найти частные производные высших порядков.


5.1.	z sin( xy),						3 z		.			5.5.	z	x4 8xy3	,
5.1.	z sin( xy),					y x2			.			5.5.	z		,
						y x2								x 2 y
5.2.	z cos(x sin y),						3 z		.			5.6.	z x2 y3 x5 y,
5.2.	z cos(x sin y),								.			5.6.	z x2 y3 x5 y,
							x2 y
5.3.	z arcrg		x y		,			2 z		.		5.7.	z arctg(2x y),
5.3.	z arcrg	1		xy	,			x y		.		5.7.	z arctg(2x y),
		1		xy				x y
5.4.	u x3 y5 (z 1)7 ,							3u			.	5.8.	z cos(7 y 5x),
5.4.	u x3 y5 (z 1)7 ,										.	5.8.	z cos(7 y 5x),
								x y z

2 z .x y

5 zx2 y3.

2 z .x y

5 z .x3 y2


5.9.	u x7 y3 (1 5z)4 ,															3u						.
5.9.	u x7 y3 (1 5z)4 ,																					.
												y x z
5.10. z 7x3					y4 5x2 y3 ,												3 z						.
5.10. z 7x3					y4 5x2 y3 ,										y2 x								.
															y2 x
5.11.	z sin(cos y x),																3 z							.
5.11.	z sin(cos y x),															x y2								.
																x y2
5.12.	z e		3 x		sin y,												5 z								.
5.12.	z e				sin y,										x2 y3										.
															x2 y3
5.13.	z x2 ln y,																	5 z								.
5.13.	z x2 ln y,														x2 y3											.
															x2 y3
5.14. z (2x 3y)5 ,																			3 z								.
5.14. z (2x 3y)5 ,																											.
																		x2 y
																			3 z
5.15.	z y	2		x	4	sin	y	3	3		x	2		,					3 z									.
5.15.	z y			x		sin	y				x			,					y x						2			.
																			y x						2
5.16.	u (7x 5y)5 z4 ,											3u									.
5.16.	u (7x 5y)5 z4 ,																				.
										z x y
5.17.	z ex2 y3 ,													2 z						.
5.17.	z ex2 y3 ,																			.
													x y

Задание 6. Вычислить приближенно.

6.1.1, 022 0, 052 .

6.2.1, 021,98 ln1, 03.

6.3.ln (0,04 3 0,993 ).

6.4.ln (4e 0,03 3,02).

6.5.(0,97) 2,02 .

6.6.(0,98) 3,05 .

6.7.1, 041,99 ln1, 02.

6.8.533е0,02 1, 01.

5.18.	z sin( y cos x),						3 z					.
5.18.	z sin( y cos x),					x y2						.
						x y2
5.19.	z y3 ln x,						5 z							.
5.19.	z y3 ln x,					y2 x3								.
						y2 x3
5.20.	z cos(x3 y3 ),								3 z				.
5.20.	z cos(x3 y3 ),												.
							x2 y
5.21.	z ln( x2		y2 ),						3 z						.
5.21.	z ln( x2		y2 ),												.
								x2 y
5.22. z (4x 3y)6 ,									3 z					.
5.22. z (4x 3y)6 ,							x2 y							.
							x2 y
5.23.	z yex ey x ,								3 z					.
5.23.	z yex ey x ,						x y2							.
							x y2
5.24.	z ln cos(x y),									3 z						.
5.24.	z ln cos(x y),															.
									x2 y
5.25.	z cos(2y x ey ),									3 z							.
5.25.	z cos(2y x ey ),									x y2							.
										x y2
		x										2 z
		x		x	,												.
5.26.	z 3 y			x
5.26.	z 3 y
				y							x y

6.9.(1,02) 3 (0,97)2.

6.10.30,98 ln1, 03.

6.11.4, 052 2, 932 .

6.12.ln ( 31, 02 30,97 1).

6.13.5е0,02 2, 032 .

6.14.(1,03) 4 (0,98)2.

6.15.(1,03) 3,98 .

6.16.е 0,01 1, 03.


6.17.	3 1, 02 ln 0,97.		6.22.	0,97 4,02 .
6.18.	ln (3e 0,02 2, 03).		6.23.	ln (e 0,02 0, 03).

6.19.	(1,02) 4,05 .		6.24.	ln ( 1, 02	0,98 1.

6.20.	3 1, 03 ln1, 02.
6.20.	3 1, 03 ln1, 02.		6.25.	3 0,97 ln1, 02.
			6.26.	ln (e 0,03 0, 02).
6.21.		3е0,08 0, 992 .	6.26.	ln (e 0,03 0, 02).

Задание 7. Написать уравнение касательной и нормали к поверхности S

в точке М.

7.1.S: z =x 2 у у2 х3, М (1, 1,0) .

7.2.S: 2x 2 3у2 z2 8xz z 6 0, М ( 1,0,1) .

7.3.S: z =3x 2 у2 , М (1,1,4) .

7.4.S: 3x 4 2у3z 3z2 xy z3x 3 0, М (1, 2,2) .

7.5.S: z = xy, М(5,1,5).

7.6.S: x 2 ху 8х z 5 0, М ( 2, 3,1) .

7.7.S: z = x 2 у2 , М ( 3,1,8) .

7.8.S: x 2 2у2 3z2 6, М (1, 1,1) .

7.9.S: z=sin ху , М ( ,1,0) .

7.10.S: x 3 у3 z3 xyz, М (1, 1, 1) .

7.11. S: z =x+y², M(0,-1,1).

7.12.S: х 8 у13 5z 7, М ( 1,1,1) .

7.13.S: z = sin (xy), M(1, 6 , 12 ).

7.14. S: z = xy +xz +yz , М (1,1,1) .

7.15.S: z = x 3 у3 , M (1, 1,0) .

7.16.S: x 3 z3 3xz 3, M (1,4,2) .

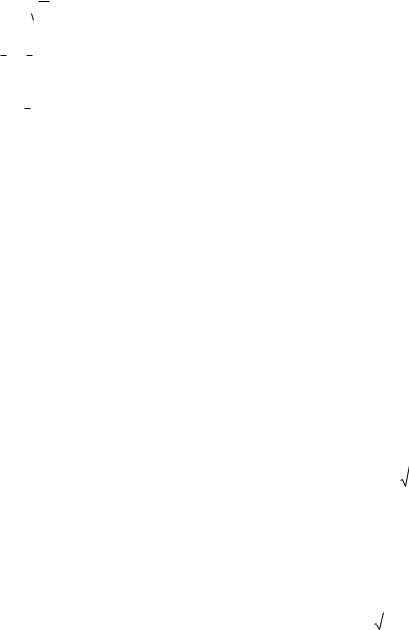
7.17.S: z = ех 2 у 1, M (1, 1,1) .

7.18.S: x 2 у2 z2 3x,(M 2,1, 1) .

7.19.S: z=x 2 у2 , M (1, 2,5) .

7.20.S: еz z xy 3, M (2,1,0) .

7.21.S: z x2 y3 xy2 5, M (2,1, 3) .

7.22.S: xy=z 2 , М (1,4, 2) .

7.23. S: z = x у х2 у 6х 3, М (0,1,2) .

уz

7.24. S: 2 z 2 x 6, M (1,2,2) .

7.25.S: z=tg х , М ( 4, , 1) .

7.26.S: х 2 у2 z2 2y, M (1,1,0) .

Задание 8. Найти градиент и производную по направлению.

8.1. Найти градиент и производную функции

u x3 yz 2 в точке Mo (1; -1; 3)

направлении вектора (2; 3; -1).

8.2. Найти градиент и производную функции

u x2 3yz 5

в точке Mo (1;2; -1)

в направлении вектора (1; -2; -1).

8.3. Найти градиент и производную функции u x ln( y2 z 2 ) в

точке

(2;1;1)

в направлении вектора a (-2;4; -3).

8.4. Найти градиент и производную функции

u x3

y 2 z 2

в точке

Mo (1; 3;4) в направлении вектора

(2; 3;3) .

8.5. Найти градиент и производную функции

z 3x4 xy y3

в точке Mо ( 1; 2)

в направлении, составляющем с осью (OX ) угол в 600 .

8.6. Найти градиент и производную функции

x 2 y

x 2

5z 2

в точке Mo

( 2;

;1)

в направлении вектора a (2;-3;4).

8.7. Найти градиент и производную функции u ln(1 x2 ) xy z

в точке

(2;2;4) в направлении вектора (1; -2; -1).

8.8. Найти градиент и производную функции

u x3 y xz 3

xyz

в точке

(1;1;1) в направлении вектора (1; -2; 3).

8.9. Найти градиент и производную функции

z x3 y x2 y3 3y 1

в точке Mo

(2;1) в направлении, идущем от этой точки к началу координат.

8.10. Найти градиент и производную функции

u y ln (1 + x 2 ) arctg z

в точке

Mo (0;1;1) в направлении вектора а

(2; 3; 2) .

8.11. Найти градиент и производную функции

x2 y2

точке Р

(1;1) в направлении биссектрисы первого координатного угла.

8.12. Найти градиент и производную функции u =

z 2 -

2 ln (x 4 y)

в точке

Mo (1;2; -1) в направлении вектора

а (3;2; 2) .

8.13. Найти градиент и производную функции

u =

+ 2 2 + 3 в

точке

Mo (1;3;2) в направлении вектора а ( 3;2; 2).

8.14. Найти градиент и производную функции

z = 5 x2 3x y 1

в точке

(2;1) в направлении, идущем от этой точки к точке N (5;5).

8.15. Найти градиент и производную функции u = xy yz zx в точке Mo (2;1;3) в направлении, идущем от этой точки к точке N (5;5;15).

8.16. Найти градиент и производную функции

= ( x 2

y 2

z 2 ) 2

в точке

Mo (0; 3;4) в направлении вектора а (2; -3;4).

8.17. Найти градиент и производную функции

x 2

xy 2 y 2

в точке

Mo ( 1;2) в направлении, составляющем с осью (OX) угол в 30 0 .

8.18. Найти градиент и производную функции

x2 y

xy z 2

в точке

Mo (1;5; 2) в направлении вектора a (2; 2;5) .

8.19. Найти градиент и производную функции

xz2

x3 y

в точке

Mo (2;2;4) в направлении вектора а(2;1; 3).

8.20. Найти градиент и производную функции

u = sin ( x + 2y) +

xyz

в точке

Mo (

;

;3) в направлении вектора а(4;3;1).

8.21. Найти градиент и производную функции

в точке

Mo (3;4)

y 2

направлении вектора а( 3; 4).

8.22. Найти градиент и производную функции

z 5x 2 y 3xy 2

в точке

Mo (1;1)

в направлении вектора а(6; 8).

8.23. Найти градиент и производную функции

z ln( 2x 3y)

в точке

Mo (2;2) в

направлении вектора а(2; 3).

8.24. Найти градиент и производную функции

z x3 y xy 2

в точке

Mo (1;3)

направлении вектора а ( 5;12).

8.25. Найти градиент и производную функции z ln(2x 4y)

в точке

Mo (1;2)

направлении вектора а(2; 3).

8.26. Найти градиент и производную функции

z arctg

в точке

Mo (-1;2)

направлении вектора а(1; 1).

Задание 9. Исследовать функцию z = f(x,y) на экстремум.

9.1.z x2 xy y2 3x 6y.

9.2.z xy 50x 20y ; x>0, y>0.

9.3.z x3 3xy2 15x 12y.

9.4.z 2x3 xy2 5x2 y2.

9.5.z 4(x y) x2 y2.

9.6. z x3 y2 (12 x y) ; x>0, y>0.

9.7.z y x 2y2 x 14y.

9.8.z x3 y2 6xy 39x 18y.

9.9.z 2x3 2y3 6xy 5.

9.10.z 2(x y) x2 y2.

9.11.z x3 3x 2y2.

9.12.z 12x x3 3y 2.

9.13.z x2 xy y2 3x 2y 1.

9.14.z 12y y3 2x2.

9.15.z x3 8y3 6xy 1.

9.16.z y x y2 x 6y.

9.17.z xy(6 x y).

9.18.z (x 5)2 y2 1.

9.19.z 1 6x x2 xy y2.

9.20.	z xy 3x2 2y2.	9.24.	z 2xy 3x2 2y2 10.
9.21.	z x3 8y3 6xy 5.	9.25. z x2 y2 xy x y.
9.22.	z x2 3( y 2)2.	9.26.	z =1+6x-2xy+3y.

9.23.z x3 y3 3xy.

Задание 10. Исследовать функцию z(x,y) на условный экстремум.

10.1. z x 2 y 2

при

x y 1.

10.13.

z x3 xy

при y x 0.

10.2.

z x3 y xy3

при

x y 1.

10.14.

z x3 15x 12y

при

x y 1.

10.3.

z x 2 y 2

при

10.15.

z y3 2x2

при

y x 1.

		.	10.16. z xy	при	x 2 y 2.
10.4. z cos2 x 2cos y при	y x	.
		2	10.17. z 2(x y) x2	при	x y 2.

10.5. z x 2 y 2

при

x y 2.

10.6.

z 1 x2

y 2

при

x y 1.

10.7. z x 2 y 2

при

10.8. z 2 x2

y 2

при

x y

10.9.

z xy

при

x y 4.

10.10. z cos2 x cos2 y при

y x

10.11.

z 3y x3

при

x y 1.

10.12.

z xy

при

x y 0.

10.18.

4 x2

y 2

при

x y 2.

10.19.

z xy

при

x y 1.

10.20.

при

5x+35y=1.

10.21. z

9 x2 y 2

при

x y 3.

10.22. z x 2 y 2

при

x y 2.

10.23. =

+ 7 при

3x+21y=1.

10.24

z 3x 2 3y 2

при

y x 1.

10.25.

z x2 xy

при

y x 1.

10.26. z

25 x2

при

x y 5.

Соседние файлы в предмете Математический анализ

#
14.09.2024335.98 Кб1TR_1_predely.pdf
#
14.09.20242.28 Mб0TR_2_proizvodnye.pdf
#
14.09.2024596.84 Кб0TR_3_issledovanie_funktsiy.pdf
#
14.09.2024440.15 Кб0TR_3_Zadacha_17.pdf
#
14.09.20241.64 Mб0TR_4_FNP.pdf
#
14.09.20242.08 Mб1Задания по теме Функции нескольких переменных - Лубенец.pdf
#
14.09.20241.75 Mб1ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКцИЙ ОДНОЙ ПЕРЕМЕННОЙ И РЯДы - ЛУБЕНЕЦ .pdf
#
14.09.202421.36 Mб0Конспект лекций по высшей математике Письменный.pdf