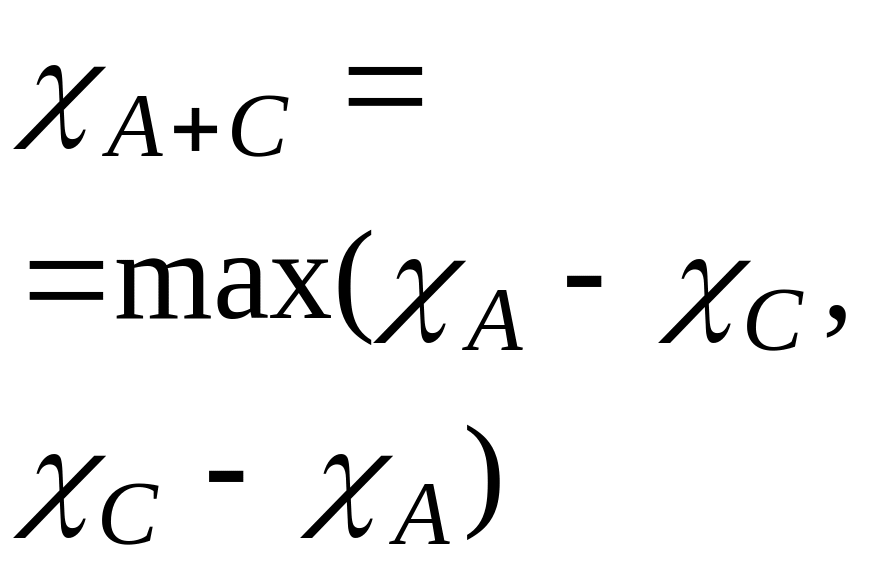DM_IDZ_Mnozhestva
.docИДЗ. Множества
Сформировать множества A,
B, C
из букв, входящих соответственно в
фамилию, имя, отчество студента. В
качестве универсального множества
принять множество U=A
B
C.
Указать мощности множеств:
.
Составить характеристические функции
.
Выполнить следующие действия:
.
Теоретический материал
Множество – совокупность элементов, обладающих двумя свойствами:
все элементы различны;
относительно каждого элемента можно сказать, принадлежит или не принадлежит он этому множеству.
Характеристическая функция множества А представляет собой п-мерный вектор, если множество конечно
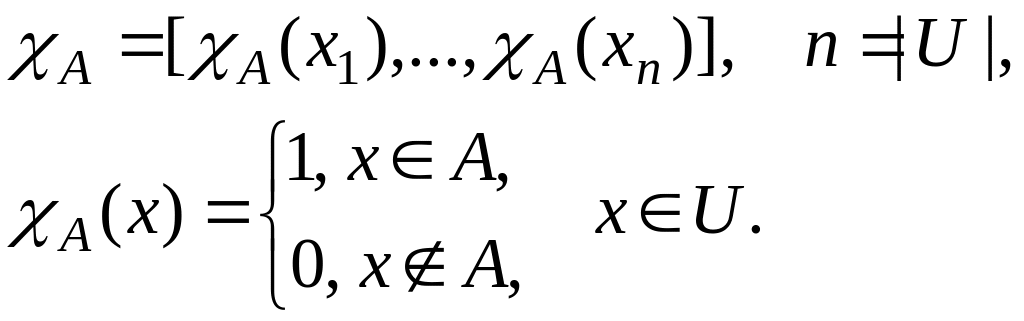
1. Объединением множеств А и В называется множество АВ, все элементы которого являются элементами множества А или В:
;
.
2. Пересечением множеств А и В называется множество АВ, элементы которого являются элементами обоих множеств А и В:
;
.
3. Абсолютным дополнением (или просто
дополнением) множества А
называется множество 
,
которое состоит из всех элементов
универсального множества U,
которые не принадлежат множеству A:
;
.
4. Относительным дополнением множества В до множества А (или разностью) называется множество А\В, которое состоит из тех элементов множества А, которые не принадлежат множеству В:
или
;
5. Симметрической разностью множеств А и В называется множество А+В:
;
.
Пример формирования множеств и характеристических функций
Иванов Кирилл Алексеевич
Формирование множеств
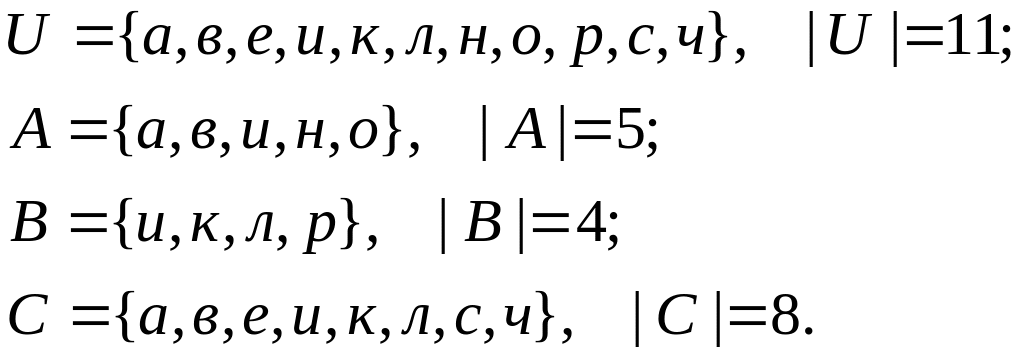
Формирование характеристических функций
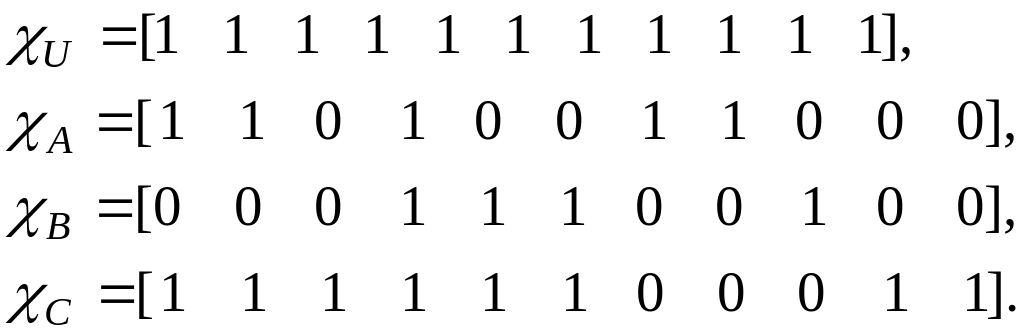
1. Объединение множеств
|
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
|
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
2. Пересечение множеств
|
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
3. Абсолютное дополнение множества
|
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
4. Разность (относительное дополнение) множеств
|
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
|
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
|
-1 |
-1 |
0 |
0 |
1 |
1 |
-1 |
-1 |
1 |
0 |
0 |
|
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
5. Симметрическая разность множеств
|
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
|
0 |
0 |
-1 |
0 |
-1 |
-1 |
1 |
1 |
0 |
-1 |
-1 |
|
0 |
0 |
1 |
0 |
1 |
1 |
-1 |
-1 |
0 |
1 |
1 |
|
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
