
Задания по дискретной математике для студентов
.pdfЗадания по дискретной математике
1.Составить множества А1, B1, C1 по буквам фамилии, имени, отчества. Составить функции характеристические для этих множеств. Выполнить операций над множествами А1, B1, C1 и над функциями характеристическими в различных сочетаниях: объединение, пересечение, абсолютное дополнение, разность, симметрическая разность.
2.Составить комплекты А2, B2, C2. Составить функций экземплярности для этих комплектов. Выполнить операций над функциями экземплярности в различных сочетаниях: объединение, пересечение, абсолютное дополнение, разность, симметрическая разность. Составить функций принадлежности нечётких множеств. Выполнить операции над нечеткими множествами в различных сочетаниях: пересечение, произведение.
3.Составить матрицы бинарных отношений:
R1={(x,y) | х – гласная буква, у – согласная буква},
R2={(x,y) | (х – гласная буква с четным порядковым номером в алфавите, у – согласная буква) или (х – согласная буква с четным порядковым номером в алфавите, у – гласная буква)},
R3={(x,y) | (х – гласная буква, у – согласная буква с нечетным порядковым номером в алфавите или гласная) или (х – согласная буква с четным порядковым номером в алфавите, у – согласная буква с четным порядковым номером в алфавите)};
х, у – буквы универсального множества, которое содержит все буквы фамилии, имени, отчества.
Выполнить над матрицами бинарных отношений в различных сочетаниях операции: объединение, пересечение, абсолютное дополнение, разность, симметрическая разность, обратное отношение.
4. По вариантам выбрать граф. Выполнить действия:
4.1. Составить таблицу дуг и присвоить метки дугам графа. 4.2. Составить матрицу смежности ориентированного графа.
4.3. Составить две матрицы инцидентности ориентированного графа.
4.4. Составить таблицу степеней вершин ориентированного графа.
4.5. Отменить ориентацию дуг орграфа, тем самым получить неориентированный граф. Составить таблицу ребер и присвоить метки ребрам графа.
4.6. Составить матрицу смежности неориентированного графа.
4.7. Составить матрицу инцидентности неориентированного графа.
4.8. Составить таблицу степеней вершин неориентированного графа.

Вариант 1
1 |
2 |
3
4 |
5 |
6
7 |
8 |
Вариант 3
1 |
2 |
3
4 |
5 |
6
7 |
8 |
Вариант 2
1 |
2 |
3
4 |
5 |
6
7 |
8 |
Вариант 4
1 |
2 |
3
4 |
5 |
6
7 |
8 |

Вариант 5 |
|
Вариант 6 |
|
1 |
2 |
1 |
2 |
|
|
|
3 |
3 |
|
|
|
4 |
5 |
4 |
5 |
|
|
|
6 |
6 |
|
|
|
7 |
8 |
7 |
8 |
|
|
Вариант 7 |
|
Вариант 8 |
1 |
2 |
1 |
2 |
3 |
3 |
4 |
5 |
4 |
5 |
6 |
6 |
7 |
8 |
7 |
8 |

Вариант 9 |
|
Вариант 10 |
1 |
2 |
|
|
1 |
2 |
3 |
|
|
|
|
3 |
4 |
5 |
|
|
4 |
5 |
6 |
|
|
|
|
6 |
7 |
8 |
|
|
7 |
8 |
|
Вариант 11 |
Вариант 12 |
|
1 |
2 |
1 |
2 |
|
|
|
3 |
|
3 |
|
|
4 |
5 |
4 |
5 |
|
|
|
6 |
|
6 |
|
|
7 |
8 |
7 |
8 |
|

Вариант 13 |
|
Вариант 14 |
|
1 |
2 |
1 |
2 |
|
|
||
3 |
|
3 |
|
|
|
|
|
4 |
5 |
4 |
5 |
|
|
||
6 |
|
6 |
|
|
|
|
|
7 |
8 |
7 |
8 |
|
|
Вариант 15 |
Вариант 16 |
|
|
1 |
2 |
1 |
2 |
|
|
3 |
|
3 |
|
|
|
4 |
5 |
4 |
5 |
|
|
6 |
|
6 |
|
|
|
7 |
8 |
7 |
8 |
|

Вариант 17
1 |
2 |
3
4 |
5 |
6
7 |
8 |
Вариант 19
1 |
2 |
3
4  5
5
6
7 |
8 |
Вариант 18
1 |
2 |
3
4  5
5
6
7 |
8 |
Вариант 20
1 |
2 |
3
4 |
5 |
|
6 |
7 |
8 |

Вариант 21
1 |
2 |
3 
4 |
5 |
6
7 |
8 |
Вариант 23
|
Вариант 22 |
1 |
2 |
|
3 |
4 |
5 |
|
6 |
7 |
8 |
|
Вариант 24 |
1 |
2 |
1 |
2 |
|
|
||
|
3 |
|
3 |
|
|
|
|
4 |
5 |
4 |
5 |
|
|
||
|
6 |
|
6 |
|
|
|
|
7 |
8 |
7 |
8 |
|
|
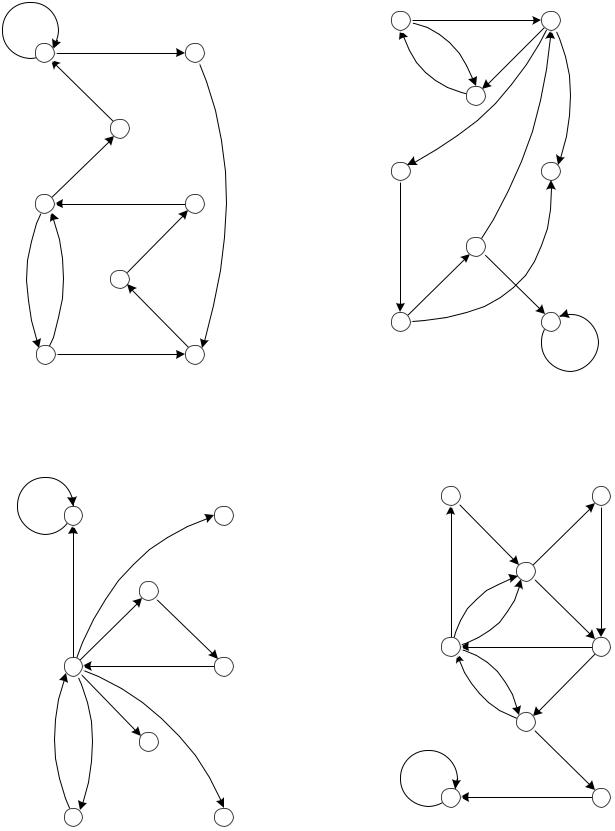
|
Вариант 25 |
Вариант 26 |
|
1 |
2 |
1 |
2 |
|
|
|
3 |
|
3 |
|
|
4 |
5 |
4 |
5 |
|
|
|
6 |
|
6 |
|
|
7 |
8 |
7 |
8 |
|
Вариант 27 |
|
Вариант 28 |
|
1 |
2 |
1 |
2 |
|
|
|
3 |
3 |
|
|
|
4 |
5 |
4 |
5 |
|
|
|
6 |
6 |
|
|
|
7 |
8 |
7 |
8 |
|

|
Вариант 29 |
1 |
2 |
|
3 |
4 |
5 |
6
7 |
8 |
Вариант 30
1 |
2 |
3
4 |
5 |
6
7 |
8 |
5.Построить по своему графу ассоциированный граф. Для ассоциированного графа построить реберный граф.
6.Для ассоциированного графа составить матрицу расстояний и найти метрические характеристики: эскцентриситеты вершин, радиус графа, диаметр графа, определить центральную (ые) вершины, периферийные вершины.
7.Для исходного ориентированного графа построить матрицу компонент сильной связности и найти компоненты сильной связности.
8.Для ассоциированного графа найти параметры связности: число вершинной связности, число реберной связности, точку(и) сочленение, мост(ы).
