Лабораторная работа №3

«Обработка результатов нескольких серий измерений (равноточные измерения)»

При многократных измерениях одной и той же величины получены две серии наблюдений по n = 12 результатов наблюдений в каждой. Вычислить результат многократных измерений.

Результаты наблюдений

Серия j = 1	Xi
	243	1,417	2,0069
	244	0,417	0,1736
	245	0,583	0,3403
	242	2,417	5,8403
	244	0,417	0,1736
	243	1,417	2,0069
	245	0,583	0,3403
	245	0,583	0,3403
	244	0,417	0,1736
	243	1,417	2,0069
	241	3,417	11,6736
	254	9,583	91,8403
	244,417

Экспериментальные данные обрабатываются в каждой j-ой серии отдельно.

1. Определяются оценки результата измерения x_j и среднеквадратического отклонения S_xj;

=

2. Обнаруживаются и исключаются ошибки для первой серии. Для этого вычисляется наибольшее по абсолютному значению нормированное отклонение:

Задавшись доверительной вероятностью Р = 0,95, с учетом q=1–Р находится соответствующее ей теоретическое (табличное) значение ν_q = 2,52 при n = 12;

Сравнивается ν₁ с ν_q. Так как ν₁ > ν_q, то данный результат измерения x₁₂ не является ошибочным.

Так как < , больше ошибочных результатов нет

3. Обнаруживаются и исключаются ошибки для второй серии:

Серия j = 2	Xi
	242	2,333	5,4444
	243	1,333	1,7778
	243	1,333	1,7778
	242	2,333	5,4444
	243	1,333	1,7778
	246	1,667	2,7778
	245	0,667	0,4444
	244	0,333	0,1111
	244	0,333	0,1111
	243	1,333	1,7778
	244	0,333	0,1111
	253	8,667	75,1111

4. Для этого вычисляется наибольшее по абсолютному значению нормированное отклонение:

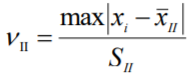
Так как ν₂ > ν_q, ν_q = 2,52 при n = 12, то данный результат измерения x₁₂ не является ошибочным.

Так как < , больше ошибочных результатов нет

5. Проверяется гипотеза о нормальности распределения для обеих серий оставшихся результатов измерений по составному критерию. Применив критерий, вычисляется отношение:

= = 0,256 = = 0,255

Задавшись доверительной вероятностью P₁ = 0,98 и для уровня значимости q₁₌1–Р₁, по таблицам определяются квантили распределения , и . Сравниваются d₁ и d₂ с и . Так как < d₁, d₂ < , то гипотеза о нормальном законе распределения вероятности результата измерения для обеих серий согласуется с экспериментальными данными.

Применив критерий 2, задаются доверительной вероятностью Р₂ = 0,99 и для уровня значимости q₂ = 1 – Р₂ с учетом n = 12 определяются по таблицам, значения m₁ = m₂ = 1 и Р*= P** = 0,99. Для вероятности Р* = 0.99 из таблиц для интегральной функции нормированного нормального распределения Ф(t), определяется значение t = 2,33 и рассчитываются:

Е₁ = t ∙ S₁ = 2,33 ∙ 3,26 = 7,595

Е₂ = t ∙ S₂ = 2,33 ∙ 3,109 = 7,244

Так не более m разностей | x_i - | превосходит Е по обеим сериям, то гипо­теза о нормальном законе распределения вероятности результата из­мерения согласуется с экспериментальными данными.

6. Проверяется значимость различия средних арифметических серий по алгоритму. Для этого вычисляются моменты закона распределения разности:

1,087

Задавшись доверительной вероятностью Р = 0,95, определяется из соответствующих таблиц интегральной функции нормированного нормального распределения Ф (t), значение t = 2,2;

Сравнивается |G| с t  S_g. Так как |G|=0,1167 t ∙ S_g = 2,2*1,2719=2,798, то различия между средними арифметическими в обеих сериях с доверительной вероятностью Р можно признать незначимым.

7. Проверяется равнорассеянность результатов измерений в сериях по алгоритму. Для этого следует определить значение:

Задавшись доверительной вероятностью Р = 0,95, определяется из соответ­ствующих таблиц значение аргумента ин­тегральной функции распределения вероятности Фишера F_q = 4,84. Сравнивается F с F_q. Так как F < F_q, то серии с доверительной вероятностью Р считают равно-рассеянными.

Так как серии однородны (равно-рассеяны с незначимым различием средних арифметических), то все результаты измерения объединяются в единый массив и выполняется обработка по алгоритму как для одной серии. Для этого определяется оценка результата измерения и среднеквадратического отклонения по формулам:

0,644

Задавшись доверительной вероятностью Р=0,95, определяется из таблиц распределения Стьюдента значение t для числа степеней свободы:

тогда t = 2,086. Определим доверительный интервал:

Δ_P = t  S = 2,086 ∙ 0,644 =1,3434