
ВЫМШАТ ЭКЗАМЕН 2 КУРС 4 СЕМЕСТР
.docxОглавление
РАЗДЕЛ I. Уравнения математической физики. 3
1. ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ 3
2. ОСНОВНЫЕ ЗАДАЧИ МАТЕМАТИЧЕСКОЙ ФИЗИКИ: 4
2.А. Волновое уравнение (Уравнение колебания струны) 5
2.Б. Уравнение теплопроводности 7
2.В. Уравнение Лапласа (или Пуассона) 9
3. МЕТОД ФУРЬЕ ДЛЯ ОДНОРОДНОГО УРАВ-Я КОЛЕБАНИЙ КОНЕЧНОЙ СТРУНЫ 10
4. МЕТОД ФУРЬЕ ДЛЯ ОДНОРОДНОГО УРАВ-Я ТЕПЛОПРОВОДНОСТИ 16
4.1. Решение при нулевых начальных условиях 16
4.2. Замечания по ряду Фурье 20
4.3. Решение при НЕ нулевых условиях 21
5. КЛАССИФИКАЦИЯ ЛИНЕЙНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ ВТОРОГО ПОРЯДКА 22
5.1. Линейное уравнение 2-го порядка 23
5.2. Собственные числа квадратной матрицы 23
5.3. КЛАССИФИКАЦИЯ уравнений 23
5.4. Следствия (уравнения ГИПЕРБОЛИЧЕСКОГО типа в канонич. виде) 24
5.5. Следствия (уравнения ПАРАБОЛИЧЕСКОГО типа в каноническом виде) 25
РАЗДЕЛ II. ТЕОРИЯ ВЕРОЯТНОСТИ 25
6. НАЧАЛЬНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ 25
6.1. Испытания и событие 25
6.2. Виды событий 25
6.3. Действия над событиями (произведение, сумма, разность) 26
6.4. Операции над событиями в диаграммах Эйлера 28
6.5. Поле событий (элементарные исходы) 29
7.1. Относительная частота и ее свойства 30
7.2. Вероятность, как функция поля событий 30
7.3. Классическое определение вероятности и ее свойства 31
7.4. Геометрическое определение вероятности 31
7.5. Схема выбора формул 32
8.1. Теорема сложения вероятностей 32
8.2. Условная вероятность 33
8.3. Теорема умножения вероятностей. 33
9.1. Формула полной вероятности 34
9.2. Теорема Байеса 35
10. Случайная величина. Функция распределения и ее свойства 35
11.1. Дискретная с.в. 36
11.2. Закон распределения д.с.в 36
11.3. Функция распределения д.с.в 37
12. Числовые характеристики дискретной с.в. и их свойства. 38
12.1. Математическое ожидание 38
12.2. Дисперсия 38
12.3. Среднее квадратическое отклонение (сигма) 39
12.4. Медиана 40
12.5. Мода 40
13. Биномиальный закон распределения дискретной с.в. 40
14. Закон Пуассона 40
15. Непрерывная с.в. и ее свойства 41
15.1. Плотность вероятности и ее свойства 42
16. Числовые характеристики н.с.в 43
17. Равномерный закон распределения 44
18. Показательный закон распределения 46
20. Закон больших чисел 51
20.1. Правило «трех сигм» 51
20.2. Неравенство Чебышева (Лемма) 52
20.3. Закон больших чисел (Теорема Чебышева) 53
21. Предельные теоремы 55
21.1. Центральная предельная теорема 55
РАЗДЕЛ III. СТАТИСТИКА 55
22. Математическая статистика 55
22.1. Основные задачи мат. статистики 55
22.2. Генеральная совокупность/выборка 56
22.3. Объем выборки 56
РАЗДЕЛ I. Уравнения математической физики.
ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
Дифференциальное уравнение в частных производных – уравнение, содержащее частные производные функции нескольких переменных
Порядок дифференциального уравнения в частных производных – порядок старшей производной, входящей в это уравнение

Решение дифференциального уравнения в частных производных – функция, имеющая все частные производные, входящие в уравнение и при подстановке в данное уравнение, обращающее его в тождество.
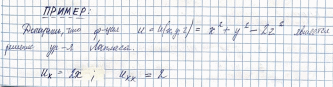
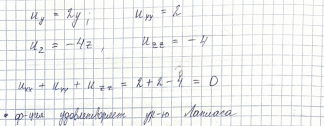
Если характеристики исследуемого процесса зависят от времени, то процесс и описывающее его уравнение, называются НЕстационарными
Стационарный процесс и описывающее его уравнение – уравнение, в котором характеристики исследуемого процесса не зависят от времени

ОСНОВНЫЕ ЗАДАЧИ МАТЕМАТИЧЕСКОЙ ФИЗИКИ:
Линейные уравнения мат. физики второго порядка:
Волновое уравнение (уравнение колебания струны)
Уравнение теплопроводности
Уравнение Лапласа (или Пуассона)
2.А. Волновое уравнение (Уравнение колебания струны)
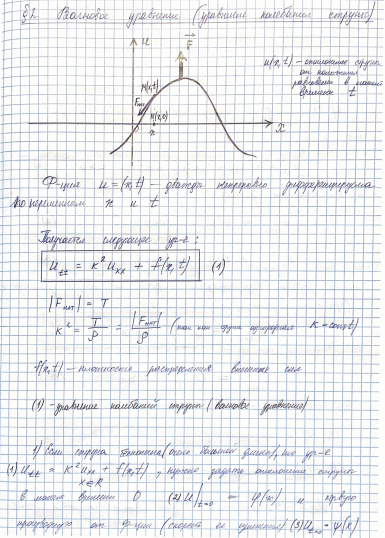


2.Б. Уравнение теплопроводности


2.В. Уравнение Лапласа (или Пуассона)

МЕТОД ФУРЬЕ ДЛЯ ОДНОРОДНОГО УРАВ-Я КОЛЕБАНИЙ КОНЕЧНОЙ СТРУНЫ







МЕТОД ФУРЬЕ ДЛЯ ОДНОРОДНОГО УРАВ-Я ТЕПЛОПРОВОДНОСТИ
4.1. Решение при нулевых начальных условиях




4.2. Замечания по ряду Фурье
4.3. Решение при НЕ нулевых условиях


КЛАССИФИКАЦИЯ ЛИНЕЙНЫХ УРАВНЕНИЙ В ЧАСТНЫХ ПРОИЗВОДНЫХ ВТОРОГО ПОРЯДКА
Линейное уравнение 2-го порядка

Матрица коэффициентов – симметрична в силу свойства aij (x) = aji (x)
Собственные числа квадратной матрицы

КЛАССИФИКАЦИЯ уравнений

Следствия (уравнения ГИПЕРБОЛИЧЕСКОГО типа в канонич. виде)

Следствия (уравнения ПАРАБОЛИЧЕСКОГО типа в каноническом виде)

РАЗДЕЛ II. ТЕОРИЯ ВЕРОЯТНОСТИ
НАЧАЛЬНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Испытания и событие

Виды событий

Действия над событиями (произведение, сумма, разность)




Операции над событиями в диаграммах Эйлера

Поле событий (элементарные исходы)


Относительная частота и ее свойства


Вероятность, как функция поля событий

Классическое определение вероятности и ее свойства

Геометрическое определение вероятности

Схема выбора формул

Теорема сложения вероятностей

Условная вероятность

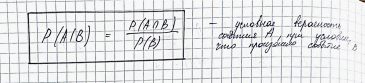
Теорема умножения вероятностей.

Формула полной вероятности


Теорема Байеса

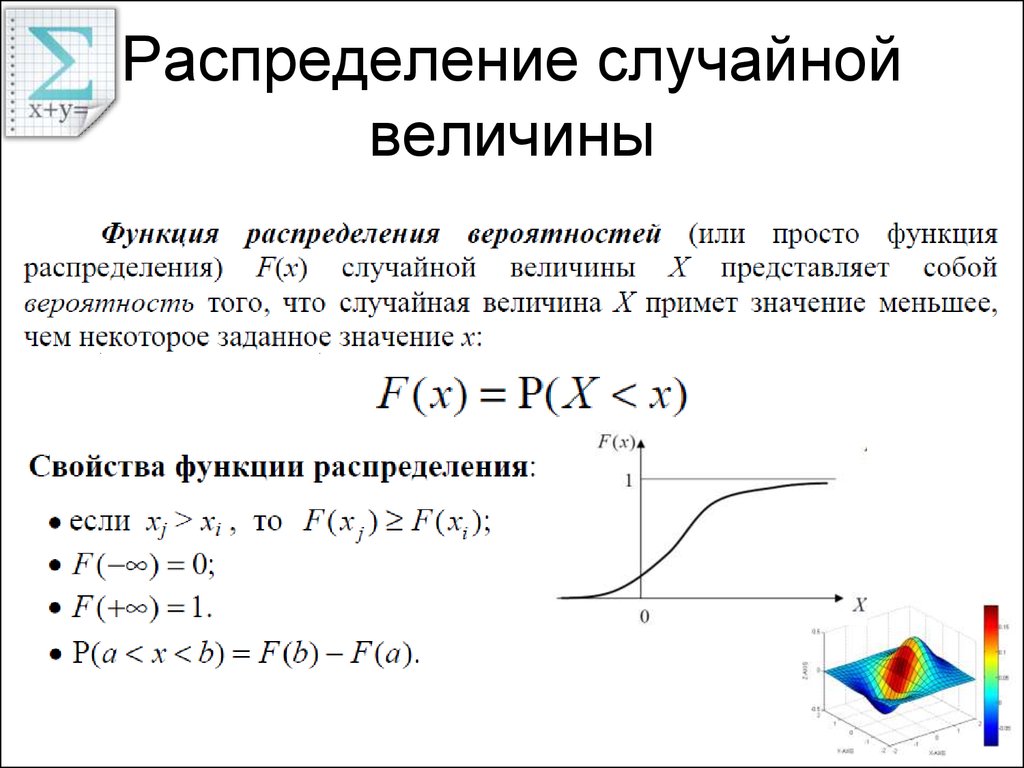
Случайная величина. Функция распределения и ее свойства

Дискретная с.в.
Случайная величина называется дискретной, если число ее возможных значений конечно или является счетным множеством.
Закон распределения д.с.в
Законом распределения дискретной случайной величины X называется соответствие между ее возможными значениями Xi и их вероятностями Pi. Его можно задать в виде таблицы:

Функция распределения д.с.в

Числовые характеристики дискретной с.в. и их свойства.
Математическое ожидание

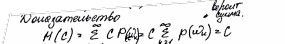
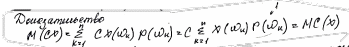
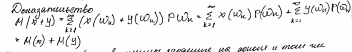
Дисперсия

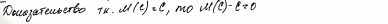
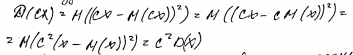

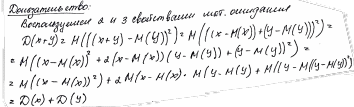
Среднее квадратическое отклонение (сигма)
![]()

Медиана
Мода
Биномиальный закон распределения дискретной с.в.

![]()
![]()
Закон Пуассона


Непрерывная с.в. и ее свойства


Плотность вероятности и ее свойства





Числовые характеристики н.с.в

Равномерный закон распределения



Показательный закон распределения
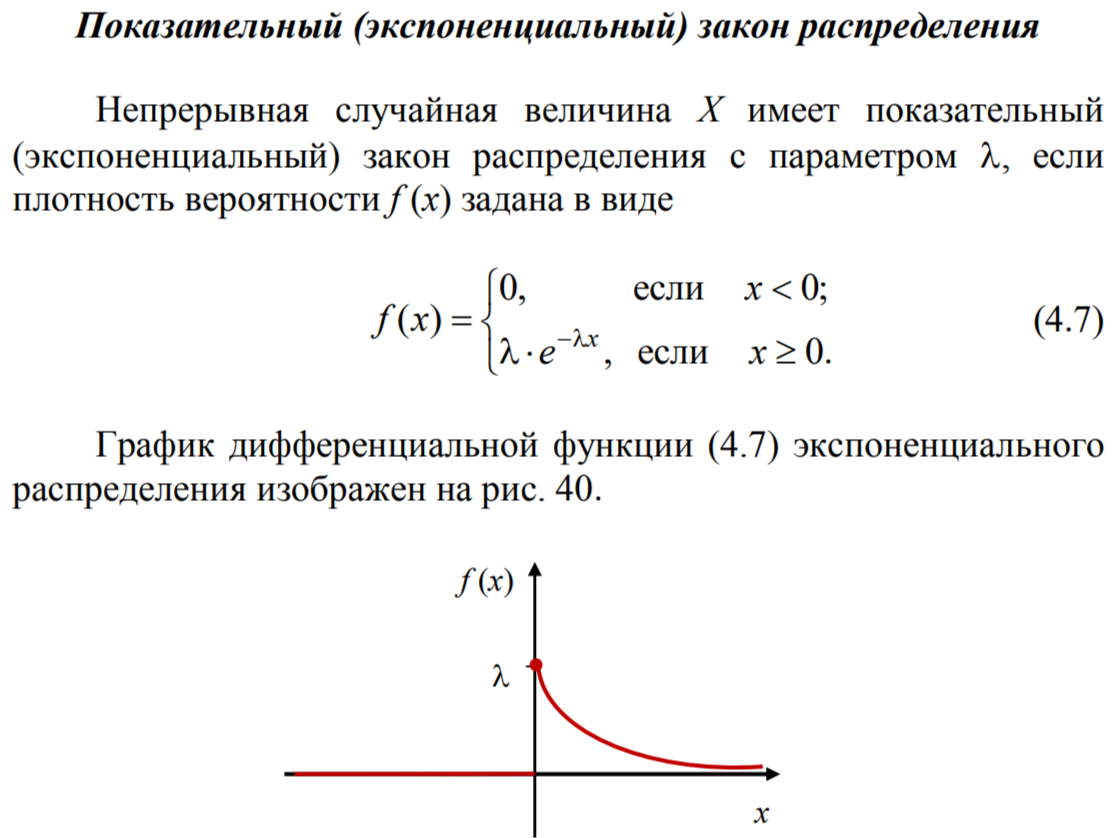



Нормальный закон распределения





Закон больших чисел
Правило «трех сигм»


Неравенство Чебышева (Лемма)

Закон больших чисел (Теорема Чебышева)


Предельные теоремы
Центральная предельная теорема

РАЗДЕЛ III. СТАТИСТИКА
Математическая статистика
Основные задачи мат. статистики

Генеральная совокупность/выборка

Объем выборки

