М
инистерство
высшего образования и науки Российской
Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
"Санкт-Петербургский Государственный архитектурно-строительный университет"
Автомобильно-дорожный факультет
Кафедра наземных транспортно-технологических машин
Дисциплина: Теория машин и механизмов
Курсовая работа по теме «Силовой, кинематический и динамический анализ плоско-рычажного механизма»
Выполнил студент: гр. 1-ЭТМКб-2
Третьяков А. Д.
Проверил преподаватель:
Виноградова Т. В.
Оценка________ «___» _______2022г.
Санкт-Петербург
2022
Оглавление
СПбГАСУ Кафедра транспортно-технологических машин |
|
Студент_________________ Группа_____________ |
|
Задание на проектирование по разделу курса «Структура, кинематика и динамика механизмов» Схема №3
Рисунок 1 – Схема №3
1 Структурный анализ механизма
Структурной особенностью данного механизма является наличие в его составе двухкратного шарнира В.
На рисунке 2 изображаем структурную схему заданного механизма.
Рисунок 2 - Структурная схема заданного механизма
Мысленно приводя в движение звено 1, убеждаемся, что при этом все точки всех подвижных звеньев механизма двигаются только во взаимно параллельных плоскостях. Следовательно, этот механизм - плоский;
По результатам моделирования движения механизма охарактеризуем все звенья механизма и все кинематические пары.
Исследуемый
механизм имеет: число подвижных звеньев
механизма n
= 5; число низших кинематических пар
,
(табл. 1.1, 1.2). Высших кинематических пар
(в данном механизме их нет).
Степень
подвижности механизма
,
определяется по формуле 1:
,
(1)
где
степень
подвижности механизма;
– число подвижных
звеньев механизма;
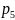– число кинематических пар пятого
класса.
Следовательно, степень подвижности механизма равна:
.
Это означает, что в рассматриваемом механизме достаточно задать закон движения только одному звену (в данном задании это звено 1, которое является ведущим), чтобы закон движения всех остальных звеньев был вполне определённым.
Из структурной схемы механизма выделяем начальный механизм - кривошип 1 со стойкой (рис. 3) 6 и ведомую кинематическую цепь (рис. 4), содержащую все остальные звенья механизма.
Анализ ведомой кинематической цепи показывает, что она состоит из двух двухзвенных структурных групп, которые соединены между собой с помощью коромысла C. Группа 2-3 (ВВВ) и группа 4-5 (ВВП).
Таблица 1.1 - Характеристика звеньев механизма
Номер звена по схеме |
Место и роль в схеме |
Характер движения |
Название |
0
|
– |
Неподвижное |
Стойка |
1
|
Входное |
Вращение вокруг О на 360° |
Кривошип |
2
|
Промежуточное |
Плоское |
Шатун |
3
|
Промежуточное |
Вращение вокруг С на угол меньше 180° |
Коромысло |
4
|
Промежуточное |
Плоское |
Шатун |
5
|
Выходное |
Поступательное прямолинейное |
Ползун |
Таблица 1.2 - Характеристика кинематических пар
Обозначение на схеме |
Вид |
Тип кинематической пары |
Подвижность пары, W |
Класс пары, S |
№ соединяемых звеньев |
О
|
В |
Низшая |
1 |
5 |
0–1 |
А
|
В |
Низшая |
1 |
5 |
1–2 |
В
|
В |
Низшая |
1 |
5 |
2–3 |
C
|
В |
Низшая |
1 |
5 |
3–0 |
D
|
В |
Низшая |
1 |
5 |
3–4 |
E
|
В |
Низшая |
1 |
5 |
4–5 |
E5
|
П |
Низшая |
1 |
5 |
5–0 |
*В – вращательная пара; П – поступательная.
Рисунок 3 – Начальный механизм
Начальный
механизм
,
определяется по формуле 2;
, (2)
где
начальный механизм.
.
Ведомая
кинематическая цепь (ВКЦ)
,
определяется по формуле 3:
, (3)
где
ведомая
кинематическая цепь;
– число подвижных
звеньев механизма.
.
.
Рисунок 4 – Ведомая кинематическая цепь
а) б)
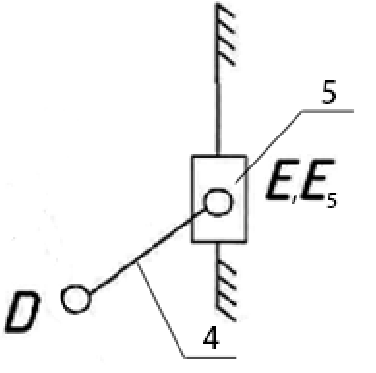
Рисунок 5 – Структурные группы механизма: а) группа 2-3 (ВВВ); б) группа 4-5 (ВВП)