Расчетно-графическое задание № 2

Линейные электрические цепи переменного тока

Для электрической цепи (рис.30) и исходных данных (табл.2) в соответствии с номером варианта выполнить следующее:

1. На основании законов Кирхгофа составить в общем виде систему уравнений для расчета токов во всех ветвях цепи, записав её в двух формах: а) дифференциальной; б) символической.

2. Определить комплексы действующих значений токов во всех ветвях, используя один из методов расчета линейных электрических цепей.

3. По результатам, полученным при выполнении п.2, определить показания ваттметра.

4. Построить топографическую диаграмму, совмещенную с векторной диаграммой токов.

5. Используя данные расчетов, полученных в п.2, записать выражение для мгновенного значения тока i3(t). Построить график указанной величины от времени.

Рис.30

Краткие теоретические сведения

При гармоническом воздействии на линейную цепь все токи и напряжения имеют форму гармонических колебаний, поэтому задача расчета цепи сводится к нахождению амплитуд и начальных фаз этих колебаний, т.е. их комплексных амплитуд.

Гармонические колебания согласно методу комплексных амплитуд могут быть представлены как проекции вектора на комплексной плоскости вращающегося против часовой стрелки с угловой частотой  (рис.31) на оси координат.

Проекция вектора на вещественную ось представляет собой мгновенное значение, выражаемое косинусоидальной функцией

, а на мнимую ось - синусоидальной функцией .

Символический вектор на комплексной плоскости математически может быть представлен в трех формах:

алгебраической

,

где ;

показательной,

где,

-модуль ; - аргумент;

тригонометрической

Рис.31.

Модуль вектора ,

аргумент .

В случае гармонического колебания аргумент комплексного числа

является функцией времени t .

Поэтому число, символизирующее вращающийся вектор, выражается:

в показательной форме ;

в тригонометрической форме

.

Таким образом, при рассмотрении напряжений и токов в цепи при гармоническом воздействии может быть построена векторная диаграмма, представляющая собой совокупность радиус-векторов, отображающих комплексные амплитуды колебаний и вращающихся на комплексной плоскости против часовой стрелки с угловой скоростью .

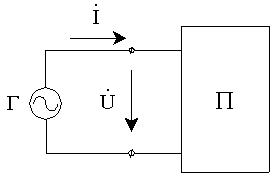
Рис.32

Поскольку взаимное расположение векторов на диаграмме не изменяется, то удобно рассматривать комплексные амплитуды напряжений и токов в момент времени t = 0.

На рис.32 приведено схематическое изображение цепи переменного тока.

Г

енератор гармонических колебаний питает пассивный двухполюсник, состоящий из сопротивлений, индуктивностей и емкостей.

Отношение комплексных амплитуд напряжения и тока на входе двухполюсника называется его комплексным входным сопротивлением:

.

Величина, обратная комплексному сопротивлению называется его комплексной проводимостью:

.

Учитывая, что и получаем

,

Отношение -полное входное сопротивление (модуль); -сдвиг фаз между напряжением и током

Как всякое комплексное число, комплексное сопротивление и комплексная проводимость могут быть представлены в показательной, алгебраической и тригонометрической формах:

,

,

- вещественная, активная составляющая;

- мнимая, реактивная составляющая комплексного сопротивления;

.

Очевидно,

, .

Если пассивный двухполюсник представляет собой активное сопротивление R, то на основании закона Ома

, ,

т. е. амплитуда тока,

а разность фаз между током и напряжением

.

Рис.33

На векторной диаграмме рис.33 напряжение и ток совпадают по фазе;

,

проводимость Yвх = 1/R.

Если пассивный двухполюсник представляет собой индуктивность, то

.

Используя метод комплексных амплитуд, получаем

.

.

Отсюда следует, что амплитуда напряжения

,

где - индуктивное сопротивление, обратная величина называется индуктивной проводимостью.

Угол сдвига фаз между напряжением и током, т.е.

ток отстает по фазе от напряжения на (рис.34).

Очевидно, что входное сопротивление индуктивности - чисто мнимая величина:

,

линейно изменяющаяся с частотой.

Рис.34

При подключении к источнику гармонического напряжения емкости в цепи потечет ток .

Используя метод комплексных амплитуд, получаем

,

.

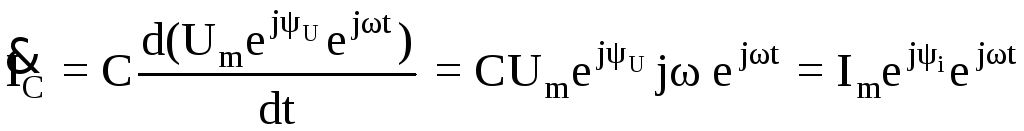Отсюда следует, что амплитуда тока в емкости

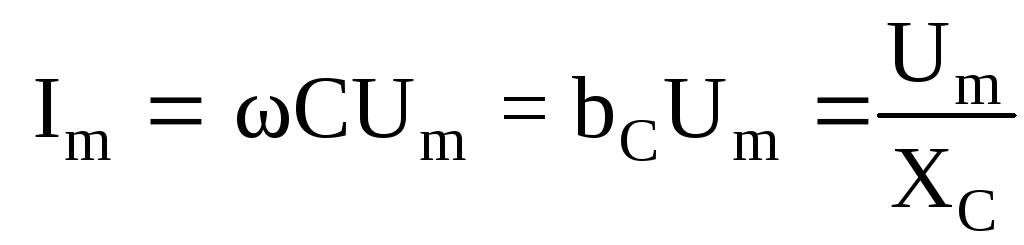, где - проводимость емкости, - емкостное сопротивление.

Сдвиг фаз между напряжением и током ,

т.е. ток опережает напряжение на  (рис.35).

Следует отметить, что входное сопротивление емкости является чисто мнимой отрицательной величиной:

, зависящей от

Рис.35 частоты источника.

Пассивный двухполюсник, состоящий из активных R и реактивных L,C элементов, имеет комплексное входное сопротивление, модуль и аргумент которого зависят от частоты генератора.

Зависимость модуля комплексного входного сопротивления цепи от частоты называется входной амплитудно-частотной характеристикой цепи (АЧХ), .

Зависимость аргумента комплексного входного сопротивления от частоты называется входной фазочастотной характеристикой цепи (ФЧХ), .

Для RL-цепи (рис.36)

Рис.36 .

Входная АЧХ последовательной RL-цепи

,

а входная ФЧХ

.

Кривые и ) показаны на рис.37,а,б.

а б

Рис.37

На основании второго закона Кирхгофа

,

где и - комплексные амплитуды

напряжений на активных и реактивных сопротивлениях.

Построим векторные диаграммы напряжений и тока, приняв в качестве исходного вектор тока, поскольку он является общим для R и L при их последовательном соединении (рис.38) .

Рис.38 Рис.39

Очевидно, что в RL-цепи ток отстает от напряжения на входе на угол

.

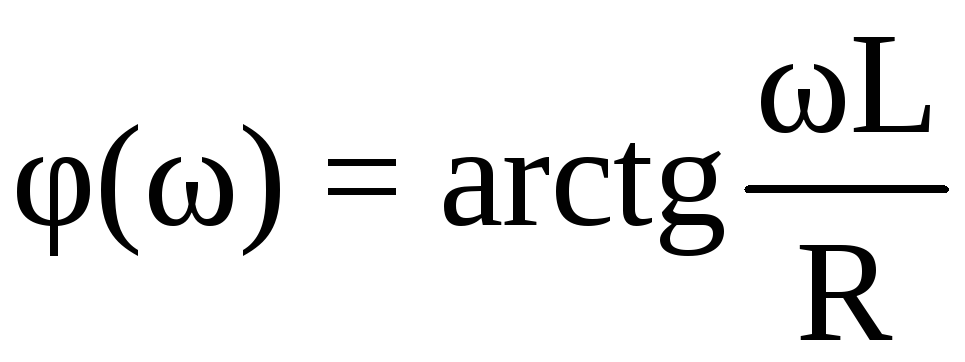Если стороны треугольника напряжений поделить на ток, то получим

или на комплексной плоскости сопротивление представляется вектором, направленным под углом  к оси вещественных величин (рис.39).

Рассматривая аналогично последовательную RC-цепь (рис.40), получим

.

Рис.40 Рис.41

Векторные диаграммы напряжений и токов приведены на рис.41.

Очевидно, в RC - цепи ток опережает напряжение на угол

.

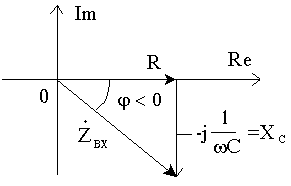
Аналогично, как и в RL-цепи, для последовательной RC-цепи можно построить на комплексной плоскости треугольник сопротивлений (рис.42).

Рис.42

.

Входная АЧХ (рис.43,а),

входная ФЧХ 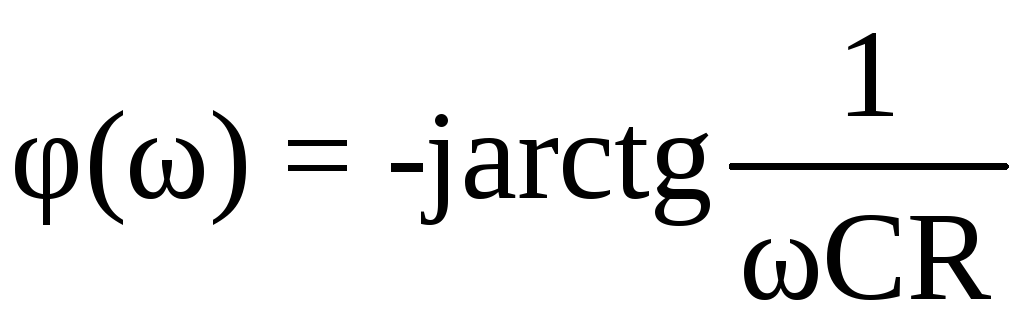(рис.43,б).

а б

Рис.43

Пример 2. Дана электрическая цепь (рис.44).

Рис.44

1. Составим на основании законов Кирхгофа систему уравнений, записав её в двух формах:

а) дифференциальной (направление токов в ветвях показано на рис.44, направление обхода контуров принято по часовой стрелке);

б) символической (методом комплексных амплитуд);

2. Определим комплексы действующих значений токов во всех ветвях, например, методом контурных токов;

Подставив в эту систему уравнений заданные ЭДС источников, параметры цепи и частоту, получим:

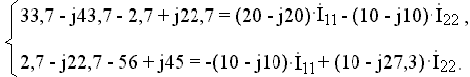
Отсюда контурные токи:

Токи в ветвях:

Рассчитаем показания ваттметра:

, где Uab и I3 - действующие значения

напряжения между узлами а и b и тока в третьей ветви.

Определим Uab.

Таким образом, действующие значения:

и показания ваттметра:

Построим топографическую диаграмму, совмещенную с векторной диаграммой токов. Примем потенциал узла а равным нулю. Тогда все точки цепи имеют потенциалы относительно узла а следующие:

Построим диаграмму токов и напряжений (рис.45).

Рис.45

Запишем выражение для мгновенного значения тока в третьей ветви:

График зависимости i3(t) приведен на рис.46.

Рис.46