
{10, 11} вопросы к экзамену 3 сем
.docxСпектральный анализ цепей при апериодическом воздействии (воздействии конечной длительности, импульсном сигнале). Частотные характеристики с точки зрения спектров.
Постановка
задачи: найти
спектры входного сигнала и выходного
сигнала (и сам выходной сигнал), зная
входной апериодический сигнал. Метод,
который использовался для описания
периодических сигналов здесь недоступен,
потому что в случае периодического
сигнала частота была фиксирована и
равна
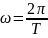 ,
но у апериодического сигнала период
можно считать бесконечным, что делает
невозможным применения ряда Фурье.
,
но у апериодического сигнала период
можно считать бесконечным, что делает
невозможным применения ряда Фурье.
Поэтому в данном случае используется другой математический аппарат – преобразование Фурье.
Общие сведения о преобразовании Фурье.
Прямое преобразование Фурье:

Где
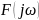 и
и
 изображение
и оригинал соответственно.
изображение
и оригинал соответственно.
Легко заметить сходство интеграла с интегралом, определяющим прямое преобразование Лапласа:
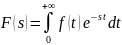
и
это неспроста: формула прямого
преобразования Лапласа может
рассматриваться как результат определенным
образом построенного обобщения
одностороннего (нижний предел не
 а
0) преобразования Фурье. Этим часто
пользуются, находя изображение по Фурье
через преобразование Лапласа.
а
0) преобразования Фурье. Этим часто
пользуются, находя изображение по Фурье
через преобразование Лапласа.
Обратное преобразование Фурье:
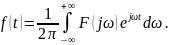
Условно факт преобразование обозначают

Замечания:
Преобразование Фурье математически «появляется» из ряда Фурье, если устремить период к бесконечности. Это как раз то, что нам нужно
Без потери общности можем считать, что сигнал определен при положительном t. Тогда достаточно применять односторонне преобразование Фурье:
 которое
можно искать из прямого преобразование
Лапласа, положив
которое
можно искать из прямого преобразование
Лапласа, положив
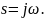
Для сходимости интеграла прямого преобразования Фурье подынтегральная функция должна быть абсолютно интегрируемой, то есть площадь модуля оригинала должна быть конечной. Таким образом, спектр имеет только абсолютно интегрируемые функции

Напомним: спектр – это комплексная функция частоты:

То есть его можно представить в показательной форме:
 где
где
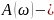 амплитудный
спектр
амплитудный
спектр
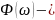 фазовый
спектр.
фазовый
спектр.
Алгоритм решения поставленной задачи.
Будем
считать, что
 входной
сигнал.
входной
сигнал.
 –
выходной
сигнал.
–
выходной
сигнал.
Н
 аходим
амплитудный и фазовый непрерывные
спектры одиночного импульса, применив
преобразование Лапласа:
аходим
амплитудный и фазовый непрерывные
спектры одиночного импульса, применив
преобразование Лапласа:

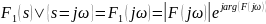
 Обоснование
непрерывности спектра следует из общего
математического описания на основе
преобразования Фурье.
Обоснование
непрерывности спектра следует из общего
математического описания на основе
преобразования Фурье.Переходим к выходному сигналу, умножив спектр на комплексную функцию цепи:
 где
принимаем
где
принимаем
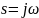


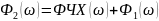
Получим выходной сигнал
 ,
применив обратное преобразование
Лапласа:
,
применив обратное преобразование
Лапласа:

Итак: Непрерывные сигналы имеют непрерывные спектры, описываются преобразованием Фурье. (Периодические сигналы имеют дискретные спектры, описываемые рядом Фурье)
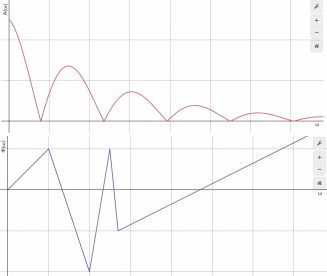
Спектральные характеристики апериодического сигнала (на примере прямоугольного импульса).
Рассмотрим прямоугольный импульс:
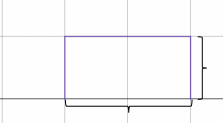
Для начала найдем аналитическое выражение для импульса (например, методом дифференцирования):
 (здесь
считаем, что сигнал начинается из нуля).
(здесь
считаем, что сигнал начинается из нуля).Найдем спектры:

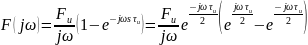
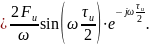 Откуда
Откуда

 где
стоит понимать, что фаза может принимать
только значения на промежутке
где
стоит понимать, что фаза может принимать
только значения на промежутке
 ,
а
,
а
 равен либо
равен либо
 либо
либо
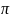 .
Для
построения найдет нули синуса:
.
Для
построения найдет нули синуса:


 Заметим,
что при нулевой частоте не определен
амплитудный спектр. Однако, неопределенность
устранимая:
Заметим,
что при нулевой частоте не определен
амплитудный спектр. Однако, неопределенность
устранимая:


