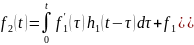частотные храктеристики+сверткаДюамеля конспект

Характеристики цепи в частотной области.

Если в передаточную функцию в виде аргумента подставить чисто мнимое число то получится частотная характеристика цепи, называема АФЧХ (Амплитудно-фазовая частотная характеристика, иногда АФХ):

комплексная функция цепи

То есть АФЧХ принимает величину (частота), на выходе получается комплексный вектор. Тогда представим АФЧХ в экспоненциальном виде:

Теперь назовем модуль амплитудно-фазовой характеристики ( – амплитудно-частотной характеристикой: А аргумент – фазо-частотно характеристикой:

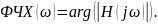
Рассмотрим пример нахождения частотных характеристик:

Пусть

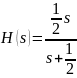
Тогда

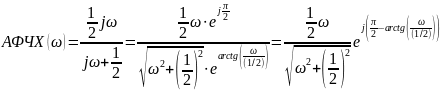
Откуда

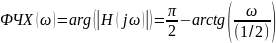
Таким образом:

1. АФХ – передаточная функция, при

2. АЧХ – модуль АФХ.

3. АФХ – аргумент АФХ.

Получение реакции цепи на произвольное воздействие.

Пусть у некоторой цепи известны характеристики в 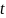- области:

Входной сигнал можно представить в виде суммы функций Хевисайда ( ) или функций Дирака 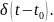Но реакции на и - соответственно. Тогда, по принципу аддитивности линейной цепи, реакция на сумму – сумма реакций. Сумма в пределе заменяется на интеграл и получаются следующий формулы:

1. Если представить входной сигнал в виде суммы функций Дирака – интеграл свертки: 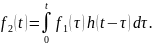Заменой в интеграле нетрудно показать, что 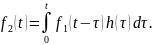Часто оказывается, что 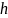- импульсная характеристика содержит функции дирака. Тогда проще вывести отдельную формулу для этого случая: Пусть 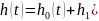(коэффициент при дельта- функции всегда равен значению переходной характеристики). Тогда: 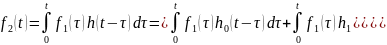Распишем отдельно второй интеграл: 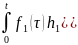Окончательно имеем 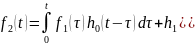Здесь мы воспользовались свойством фильтрации дельта- функции и тем фактом, что производная функции Хевисайда есть функция Дирака.

2. Если представить входной сигнал в виде суммы функций Хевисайда – интеграл Дюамеля: