
Федеральное государственное автономное образовательное учреждение высшего образования «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ»
им. В. И. Ульянова (Ленина)»
Кафедра ТОЭ
ОТЧЕТ
По лабораторной работе № 8
«ИССЛЕДОВАНИЕ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ДВУХПОЛЮСНИКОВ»
Выполнил: Иванов С. К
Группа № 0392
Преподаватель: Езеров К. С
Вопросы |
Задачи ИДЗ |
Даты коллоквиума |
Итог |
|||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
||||||||||
|
||||||||||
|
||||||||||
|
||||||||||
Санкт-Петербург, 2022
Цель работы: исследование амплитудно-частотных и фазочастотных
характеристик входных сопротивлений
 -
и
-
и
 -двухполюсников.
-двухполюсников.
8.1. Подготовка к работе
В работе необходимо исследовать частотные
характеристики реактивного
 двухполюсника
и
двухполюсника
и
 двухполюсника,
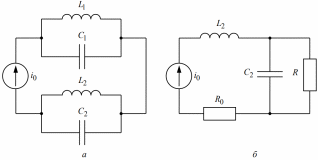
схемы которых представлены
двухполюсника,
схемы которых представлены
на

При действии на цепь ИТ реакцией является напряжение на входе, и
свойства пассивного ДП в установившемся синусоидальном режиме определяются входным сопротивлением

График модуля
 построенный в виде функции от частоты
построенный в виде функции от частоты
 ,
является в данном случае АЧХ, график
аргумента
,
является в данном случае АЧХ, график
аргумента –
ФЧХ, а графики
–
ФЧХ, а графики
 и
и
 – соответственно вещественной и мнимой
частотными характеристиками ДП.
Используют также АФХ, представляющую
собой геометрическое место значений Z
j
, построенное в комплексной плоскости,
например по графикам АЧХ и ФЧХ.
– соответственно вещественной и мнимой
частотными характеристиками ДП.
Используют также АФХ, представляющую
собой геометрическое место значений Z
j
, построенное в комплексной плоскости,
например по графикам АЧХ и ФЧХ.
При резонансе в пассивном ДП выполняется
условие
 или
или ,
т. е. на резонансной частоте
,
т. е. на резонансной частоте
 в установившемся синусоидальном режиме
ток и напряжение ДП совпадают по фазе:
в установившемся синусоидальном режиме
ток и напряжение ДП совпадают по фазе:
 .
.
Для двухполюсника входное сопротивление будет мнимой нечетной дробно-рациональной функцией :

Нули
 и полюсы
и полюсы
 сопротивления
,
определяемые соответственно из условия
резонанса напряжений
сопротивления
,
определяемые соответственно из условия
резонанса напряжений
 и
условия резонанса токов
и
условия резонанса токов
 ,
совпадают с резонансными частотами
двухполюсника.
Они являются мнимыми числами и
располагаются, чередуясь друг с другом,
на оси
,
совпадают с резонансными частотами
двухполюсника.
Они являются мнимыми числами и
располагаются, чередуясь друг с другом,
на оси
 плоскости
комплексной частоты
плоскости
комплексной частоты
 .
В зависимости от структуры и элементов
цепи в начале координат располагается
либо нуль, как в
.
В зависимости от структуры и элементов
цепи в начале координат располагается
либо нуль, как в
 либо полюс. Для неприводимых цепей общее
число резонансов напряжений и токов на
единицу меньше количества реактивных
элементов.
либо полюс. Для неприводимых цепей общее
число резонансов напряжений и токов на
единицу меньше количества реактивных
элементов.
Используя указанные свойства реактивных
ДП, а также свойство
 ,
можно построить частотные характеристики
,
можно построить частотные характеристики
 качественно.
Например, для ДП, изображенного на рис.
8.1, а, частотная характеристика jx
, приведенная на
качественно.
Например, для ДП, изображенного на рис.
8.1, а, частотная характеристика jx
, приведенная на
 ,
может быть построена качественно для
,
может быть построена качественно для ,
исходя из следующих соображений: в цепи
возможны лишь 3 резонансные частоты
,
исходя из следующих соображений: в цепи
возможны лишь 3 резонансные частоты ;
предельные значения сопротивления
;
предельные значения сопротивления
 и
и
 оцениваются посредством анализа
эквивалентной схемы замещения при
оцениваются посредством анализа
эквивалентной схемы замещения при
 и
и
 .
.

АЧХ этого идеализированного
двухполюсника
определяется модулем функции, изображенной
на рис. 8.2, поскольку
 .
АЧХ ДП с реальными катушками индуктивности
и конденсаторами, полученная опытным
путем, не принимает нулевых и бесконечно
больших значений; она является непрерывной
функцией частоты, но при высокой
добротности контуров, исследуемых в
работе
.
АЧХ ДП с реальными катушками индуктивности
и конденсаторами, полученная опытным
путем, не принимает нулевых и бесконечно
больших значений; она является непрерывной
функцией частоты, но при высокой
добротности контуров, исследуемых в
работе
 ,
сохраняет большую крутизну в области
резонансных значений частоты.
,
сохраняет большую крутизну в области
резонансных значений частоты.
Для
-двухполюсников
в зависимости от соотношения значений
параметров
 резонанс может и не наблюдаться. Следует
также отметить, что в
-двухполюсниках
частоты, соответствующие максимальным
и минимальным значениям
резонанс может и не наблюдаться. Следует
также отметить, что в
-двухполюсниках
частоты, соответствующие максимальным
и минимальным значениям ,
в общем случае не совпадают с резонансными.
,
в общем случае не совпадают с резонансными.
Перед экспериментальным исследованием выполним расчетное задание, необходимое для контроля опытных данных:
Вычислим резонансные частоты -двухполюсника, изображенного на
 ,
,
 :
:


 Построим
АЧХ для данного контура, учитывая, что
Построим
АЧХ для данного контура, учитывая, что


Рассчитаем резонансную частоту для - двухполюсника

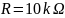
 То
есть резонанс возможен.
Построим
АЧХ:
То
есть резонанс возможен.
Построим
АЧХ:
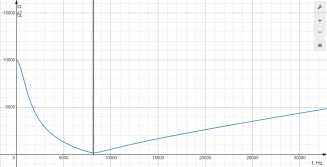

 Резонанс
невозможен.
Резонанс
невозможен.
Построим АЧХ:



8.2. Экспериментальные исследования.
Исследование частотных характеристик - двухполюсника. Используется схема
 ,
амплитуда входного сигнала
,
амплитуда входного сигнала
 Результаты
измерений можно наблюдать в протоколе
наблюдений, таблица 1
Результаты
измерений можно наблюдать в протоколе
наблюдений, таблица 1
 Построим
АЧХ и ФЧХ по результатам измерений
(на одном графике с теоретическими
значениями):
Построим
АЧХ и ФЧХ по результатам измерений
(на одном графике с теоретическими
значениями):

 Полученная
опытным путем АЧХ не принимает
нулевых и бесконечно больших значений,
она является непрерывной функцией
частоты. Но сохраняет большую крутизну
в области резонансных значений частоты
благодаря высокой добротности.
Теоретически,
все векторы
Полученная
опытным путем АЧХ не принимает
нулевых и бесконечно больших значений,
она является непрерывной функцией
частоты. Но сохраняет большую крутизну
в области резонансных значений частоты
благодаря высокой добротности.
Теоретически,
все векторы
 должны лежать на оси
должны лежать на оси
 в силу того, что сопротивление цепи при
любой частоте должно быть чисто мнимым.
На практике это правило не соблюдается
из-за неидеальности схемы (более того,
АЧХ измеряется на резисторе в
в силу того, что сопротивление цепи при
любой частоте должно быть чисто мнимым.
На практике это правило не соблюдается
из-за неидеальности схемы (более того,
АЧХ измеряется на резисторе в
 ,
что сказывается на результате):
,
что сказывается на результате):

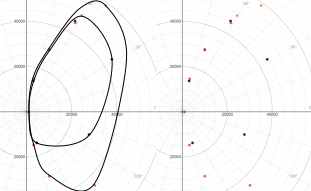
 Тем
не менее, по результатам эксперимента
имеем следующую АФЧХ:
Тем
не менее, по результатам эксперимента
имеем следующую АФЧХ:
 Вопрос
1:
В чем отличие частотных
характеристик реальной цепи, составленной
из катушек индуктивности и конденсаторов,
от характеристик идеальных реактивных
ДП?
Ответ:
Идеальный реактивный
двухполюсник обладает чисто мнимым
сопротивлением, которое можно представить
в виде
Вопрос
1:
В чем отличие частотных
характеристик реальной цепи, составленной
из катушек индуктивности и конденсаторов,
от характеристик идеальных реактивных
ДП?
Ответ:
Идеальный реактивный
двухполюсник обладает чисто мнимым
сопротивлением, которое можно представить
в виде
 где
степень
выбирается исходя из того, какой из
резонансов наблюдается первым. Таким
образом, теоретический максимум и
минимум модуля сопротивления
где
степень
выбирается исходя из того, какой из
резонансов наблюдается первым. Таким
образом, теоретический максимум и
минимум модуля сопротивления
 и
и
 соответственно, что не достигается в
реальных цепях.
Вопрос 2:
Как
проконтролировать полученные АЧХ
и ФЧХ по эквивалентным схемам цепи
при
соответственно, что не достигается в
реальных цепях.
Вопрос 2:
Как
проконтролировать полученные АЧХ
и ФЧХ по эквивалентным схемам цепи
при
 Ответ
2:
При нулевой и стремящейся к
бесконечности частотах можно
воспользоваться комплексными схемами
замещения. В обоих случаях получим
короткое замыкание вместо двухполюсника,
что значит, что АЧХ
Ответ
2:
При нулевой и стремящейся к
бесконечности частотах можно
воспользоваться комплексными схемами
замещения. В обоих случаях получим
короткое замыкание вместо двухполюсника,
что значит, что АЧХ АЧХ
АЧХ Резонансные
частоты – полюсы
Резонансные
частоты – полюсы
 откуда
следует, что при
откуда
следует, что при
 в
АЧХ будут наблюдаться локальные
максимумы (разрывы второго рода для
идеальной цепи).
в
АЧХ будут наблюдаться локальные
максимумы (разрывы второго рода для
идеальной цепи).
Исследование частотных характеристик - двухполюсника, в котором резонанс возможен. Измерения производятся на схеме, изображенной на рис
 при
при
 Результаты измерений занесены в
таблицу 2.
Произведём построения,
аналогичные п1:
Результаты измерений занесены в
таблицу 2.
Произведём построения,
аналогичные п1:



Вопрос 3: Можно ли по частотным характеристикам (АЧХ, ФЧХ, АФХ)
определить резонансные частоты ДП? По каким признакам?
Ответ: Да, можно. Условие резонанса для сложной цепи или участка цепи со смешанным соединением нескольких индуктивных емкостных и резистивных (активных) элементов, заключающееся в равенстве нулю мнимой части входного сопротивления или мнимой части входной проводимости цепи. При резонансных частотах наблюдается локальный максимум АЧХ (важно то, что в общем случае при не глобальный максимум). Важной оговоркой в определении резонанса является то, что резонанс – состояние цепи или части цепи. Это означает, что разность фаз при резонансе в общем случае не обнуляется, то есть полностью активное сопротивление не имеет место.
Тем не менее, в исследуемой цепи проконтролировать резонанс можно как по АЧХ (минимум графика, поскольку последовательное соединение и, следовательно, резонанс напряжений), так и по ФЧХ (цепь второго порядка, возможен только один резонанс, наблюдается нулевая разность фаз, т. е. входное сопротивление чисто активное).
Исследование частотных характеристик RLC-двухполюсника, в котором резонанс невозможен. Исследуется схема, аналогичная п2.
 Результаты измерений занесены в таблицу
2.
Произведем необходимые
построения:
Результаты измерений занесены в таблицу
2.
Произведем необходимые
построения:


 Вопрос
4:
В чем причина отсутствия
резонанса в исследуемой
цепи и какие из графиков (АЧХ, ФЧХ
или АФХ) об этом свидетельствуют?
Ответ:
Выведем
формулу для резонанса.
Вопрос
4:
В чем причина отсутствия
резонанса в исследуемой
цепи и какие из графиков (АЧХ, ФЧХ
или АФХ) об этом свидетельствуют?
Ответ:
Выведем
формулу для резонанса.


 Откуда
получаем уже известное условие резонанса
Откуда
получаем уже известное условие резонанса
 То
есть при определенных
То
есть при определенных
 подкоренное выражение обращается в
ноль, следовательно, резонансной частоты
не существует. Физически это можно
объяснить тем, что при малых сопротивлениях
(а именно, меньших, чем
подкоренное выражение обращается в
ноль, следовательно, резонансной частоты
не существует. Физически это можно
объяснить тем, что при малых сопротивлениях
(а именно, меньших, чем
 ) цепь имеет индуктивный характер при
любой частоте вследствие того, что
сопротивление «нейтрализует» действие
ёмкости.
Вопрос 5:
Как
проконтролировать АЧХ, ФЧХ и АФХ
цепи при
) цепь имеет индуктивный характер при
любой частоте вследствие того, что
сопротивление «нейтрализует» действие
ёмкости.
Вопрос 5:
Как
проконтролировать АЧХ, ФЧХ и АФХ
цепи при
 ?
Ответ:
При
воспользуемся
схемой замещения:
?
Ответ:
При
воспользуемся
схемой замещения:
 то есть
АЧХ
то есть
АЧХ ФЧХ
ФЧХ (очевидно, что это точка
(очевидно, что это точка
 )
) то
есть АЧХ
то
есть АЧХ ,
ФЧХ
,
ФЧХ .
.
Выводы:
В ходе лабораторной работы были исследованы амплитудно-частотные и фазочастотные характеристики входных сопротивлений - и -двухполюсников.
