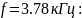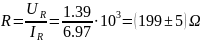Лабы (4 сем) / Иванов_Серафим_0392_6

Федеральное государственное автономное образовательное учреждение высшего образования «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ»

им. В. И. Ульянова (Ленина)»

Кафедра ТОЭ

ОТЧЕТ

По лабораторной работе № 6

«ИССЛЕДОВАНИЕ УСТАНОВИВШЕГОСЯ СИНУСОИДАЛЬНОГО

РЕЖИМА В ПРОСТЫХ ЦЕПЯХ»

Выполнил: Иванов С. К

Группа № 0392

Преподаватель: Езеров К. С

Вопросы		Задачи ИДЗ					Даты коллоквиума		Итог

Санкт-Петербург, 2022

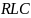Цель работы: практическое ознакомление с синусоидальными режимами в простых -, - и - цепях.

6.1. Подготовка к работе.

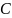При анализе электрических цепей в установившемся синусоидальном режиме важно помнить амплитудные и фазовые соотношения между токами и напряжениями элементов цепи: ток в -элементе совпадает по фазе с напряжением, ток в -элементе отстает, а в -элементе опережает напряжение на четверть периода . Следует учитывать, что комплексные сопротивления индуктивности и емкости есть функции частоты:

Следовательно, комплексные сопротивления -, - и - цепей функции частоты. Так, для -цепи, изображенной на рис. 6.1, в, комплексное сопротивление

Реактивная составляющая этого сопротивления равна разности модулей индуктивного и емкостного сопротивлений и поэтому может принимать различные знаки: если она положительна, реакция цепи имеет индуктивный характер, если отрицательна – емкостный, если обращается в нуль ( ), цепь будет находиться в состоянии резонанса.

Как модуль и аргумент комплексного сопротивления

так и определяемые ими по закону Ома действующее значение и начальная

фаза тока

зависят от соотношения значений индуктивного и емкостного сопротивлений.

Токи и напряжения цепи в установившемся синусоидальном режиме наглядно представляют с помощью векторной диаграммы. Такая диаграмма для -цепи приведена на рис. 6.2 а, где рассматривается случай , т. е. ток опережает напряжение на , что соответствует емкостной реакции и временной диаграмме, представленной на рис. 6.2 б.

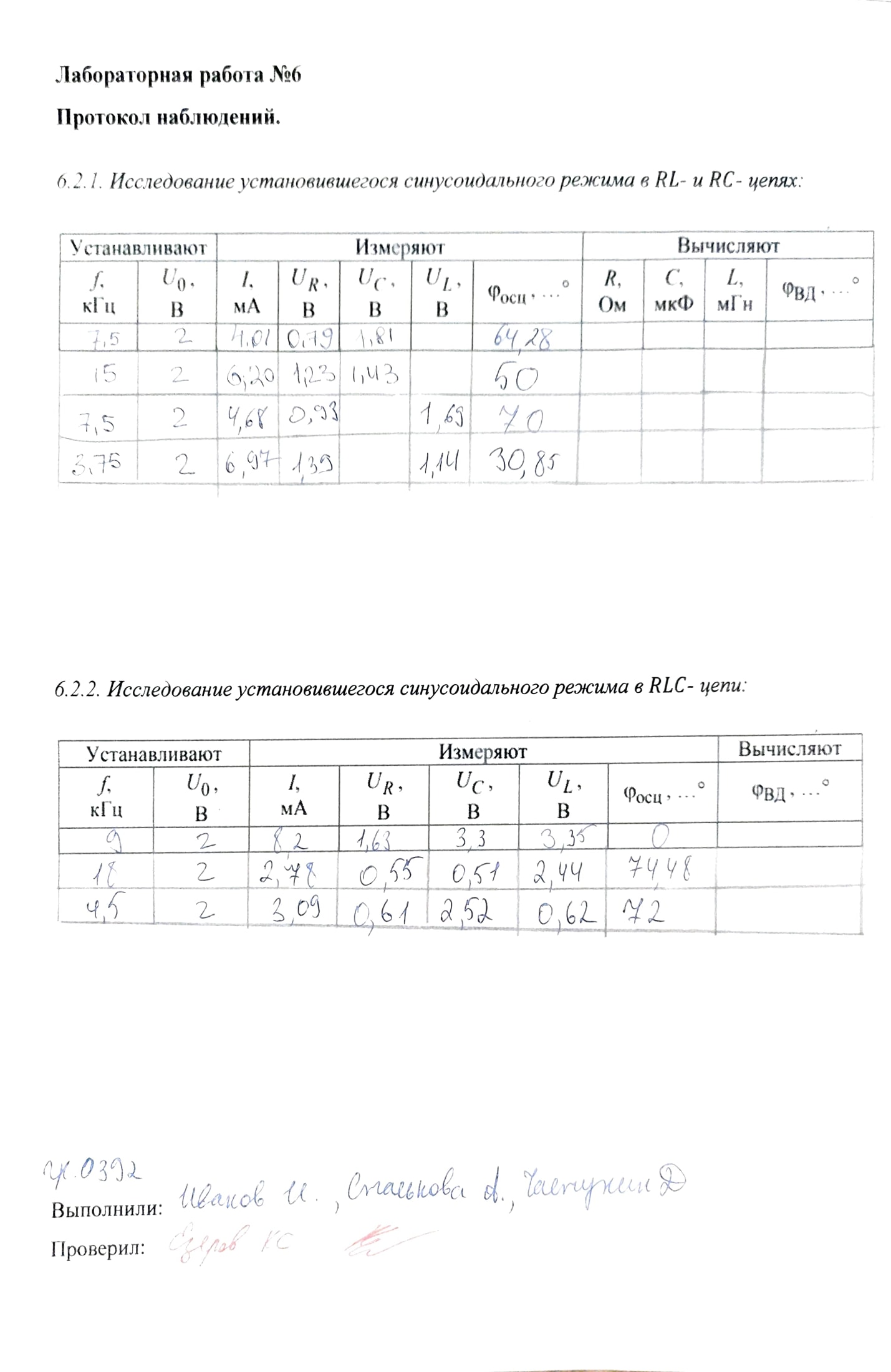
6.2. Экспериментальные исследования и обработка результатов.

Для выполнения работы использовалась катушка индуктивности, конденсатор и набор резисторов. Источником питания служил ГС. Осциллограммы напряжения и тока снимались с помощью осциллографа.

6.2.1. Исследование установившегося синусоидального режима в RL- и RC-цепях.

6.2.1.C-

Собрана схема 6.3, где сопротивление резистора, включаемого параллельно выходу ГС для приближения свойств последнего к свойствам идеального ИН.

Напряжение на выходе установлено на частоты ГС

Результаты измерений тока и напряжений 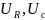, а также результат вычисления угла можно наблюдать в протоколе наблюдений.

Получим аналитическое выражение для , в случае схемы 6.3.

Замечание: известно, что 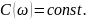Значит, должно быть равным для всех экспериментов.

Рассчитаем :

1. 

2. 

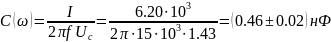
Значения ёмкости совпали с точностью до погрешности.

Получим аналитическое выражение для

1. 

2. 

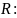
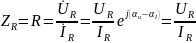
Значения сопротивлений совпали с точностью до допустимой погрешности.

Построим векторную диаграмму (качественно):

Найдем по ВД значение угла

1. Для упрощения вычислений можем сдвинуть фазу на Откуда что совпадает с измеренными значениями с точностью до погрешности в .

2. Аналогично п1 избавимся от 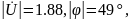что совпадает с измеренными значениями с точностью до погрешности в для модуля и фазы соответственно.

6.2.1 Вопросы:

1. Почему Ответ: потому что это только модули соответствующих напряжений, в законе Кирхгофа для комплексных напряжения суммируются векторы (комплексные числа):

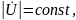
2. Почему с ростом частоты значения и увеличились, а и уменьшились? Ответ: потому что с ростом частоты уменьшается комплексное сопротивление ёмкости , а значит уменьшается и модуль комплексного сопротивления. С другой стороны, причем Но модуль входного сопротивления уменьшился, а значит, модуль тока увеличился. Отсюда очевидно, что тоже увеличится. 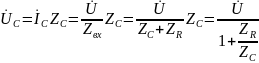откуда ясно, что при уменьшении модуля тоже уменьшится. Из геометрических соображений: вектор стал длиннее, вектор короче, все углы, кроме сохранились. Следовательно, уменьшился. что было доказано аналитически и подтверждено экспериментально.

6.2.1.L-

Собрана схема 6.4, где сопротивление резистора, включаемого параллельно выходу ГС для приближения свойств последнего к свойствам идеального ИН.

Напряжение на выходе установлены на частоты ГС

Результаты измерений тока и напряжений , а также результат вычисления угла можно наблюдать в протоколе наблюдений.

Получим аналитическое выражение для , в случае схемы 6.4.

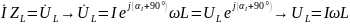
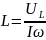
Замечание: известно, что Значит, должно быть равным для всех экспериментов.

Рассчитаем :

1. 

2. 

Значения индуктивности совпали с точностью до погрешности.

Для расчета воспользуемся уже готовыми формулами, выведенными в пунктах для

1. 

2. 

Значения сопротивлений совпали как внутри данной серии экспериментов, так и между данной серией и серией с емкостью.

Построим векторную диаграмму (качественно):

Найдем по ВД значение угла

1. Для упрощения вычислений можем сдвинуть фазу на Откуда что совпадает с измеренными значениями с погрешностью в 4% и 13% соответственно.

2. что совпадает с измеренными значениями с погрешностью в 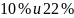соответственно.

1. Вопросы:

3. Почему Ответ: потому что это только модули соответствующих напряжений, в законе Кирхгофа для комплексных напряжения суммируются векторы (комплексные числа):

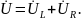
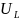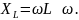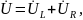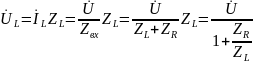4. Почему с уменьшением частоты значения и увеличились, а и уменьшились? Ответ: с уменьшением частоты уменьшается комплексное сопротивление ёмкости С другой стороны, причем Но модуль входного сопротивления уменьшился, а значит, модуль тока увеличился. Отсюда очевидно, что тоже увеличится. откуда ясно, что при уменьшении модуля тоже уменьшится. Из геометрических соображений: вектор стал длиннее, вектор 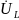короче, все углы, кроме сохранились. Следовательно, уменьшился. что было доказано аналитически и подтверждено экспериментально.

6.2.2. Исследование установившегося синусоидального режима в RLC-цепи

Собрана схема 6.5.

На выходе ГС установлено напряжение . По фигуре Лиссажу, полученной на экране осциллографа после включения режима определена точка резонанса:

Построим ВД для цепи (качественно):

1. Резонанс:

2. Индуктивный режим

3. Ёмкостной режим

Проведя рассуждения, аналогичные рассуждениям в предыдущих пунктах, получим аналогичные аналитические выражения. Из них

1. 

2. 

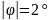
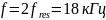
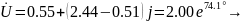
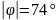
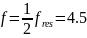
3. Для всех частот значения углов совпали с точностью до допустимой погрешности.

Вопросы:

5. Почему 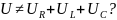Ответ: потому что для получения равенства необходимо складывать комплексные напряжения, а не их модули. По закону второму закону Кирхгофа можно получить, что

6. Почему при уменьшении и увеличении частоты относительно резонансной уменьшаются, увеличивается? Ответ: Максимум тока при последовательном соединении достигается при При выполнении условия, входное сопротивление становится чисто действительным, а значит, т. к. ,

Вывод:

практически ознакомились синусоидальными режимами в -, -, -цепях.