Нелинейные СУ (6 семестр) / Лабы по нелинейным СУ / Лаб5 / Лаб5_0392_ИвановСтаськоваЧастухин

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В. И. Ульянова (Ленина)

Кафедра АПУ

отчет

по лабораторной работе №5

по дисциплине ТАУ

Тема: Анализ устойчивости положения равновесия

Студенты гр. 0392		Иванов С. К.
		Стаськова А. Р.
		Частухин А. Р.
Преподаватель		Жеронкин К. М.

Санкт-Петербург

2023

Цель работы.

Анализ устойчивости нелинейных систем методами Ляпунова.

Выполнение работы.

Задание 1. Проанализируем первым методом Ляпунова нелинейный осциллятор, заданный системой дифференциальных уравнений.

У системы единственное положение равновесия в точке (0, 0).

Матрица состояний линеаризованной системы:

ХП: . Собственные значения центр.

Собственные значения лежат на мнимой оси. В этом критическом случае по линеаризованной модели нельзя судить об устойчивости положения равновесия нелинейной системы.

В данном примере первый метод Ляпунова не позволяет судить об устойчивости положения равновесия. Обратимся ко второму методу Ляпунова.

Введём положительно-определённую функцию

Продифференцируем её по времени

Получили отрицательно-определённую функцию, что означает асимптотическую устойчивость. Так как , то положение равновесия устойчиво в целом.

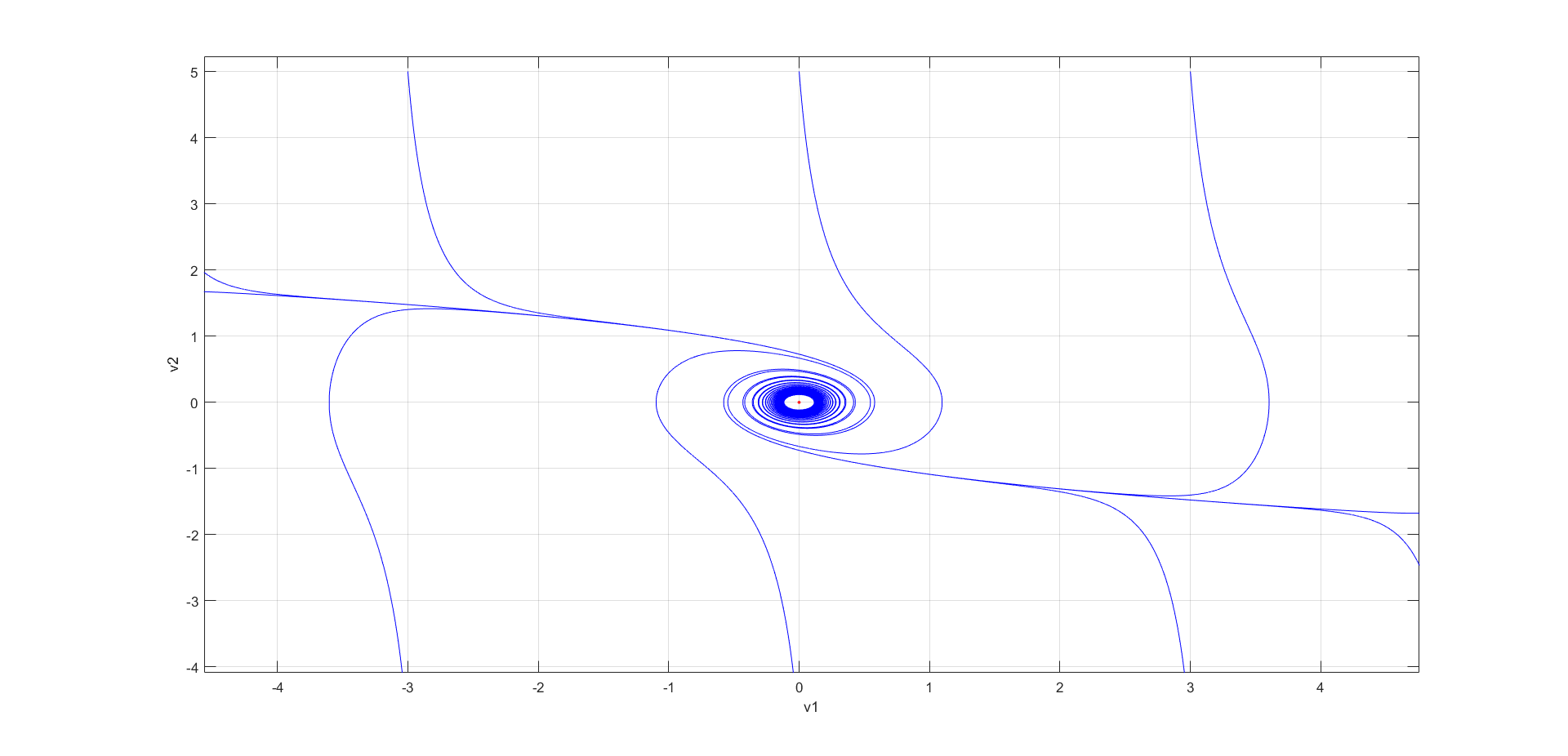
Рис.1 Фазовый портрет осциллятора

Задание 2.

Проанализируем первым методом Ляпунова систему, заданную структурной схемой:

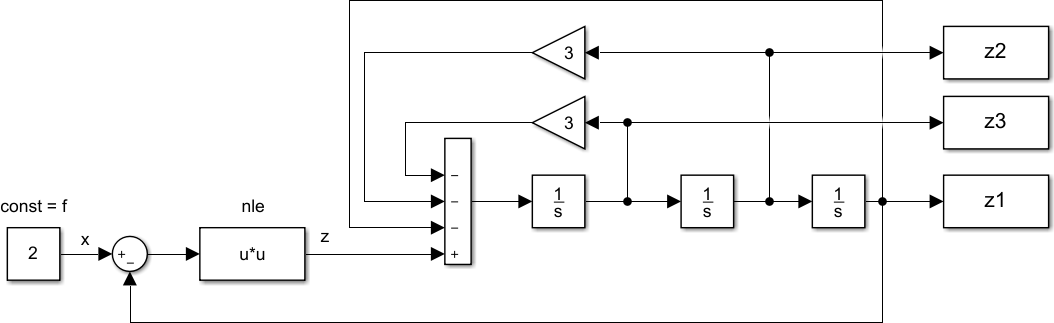
Рис. 2 Структура модели

Система ДУ данной системы:

Положение равновесия в точках (1, 0, 0) и (4, 0, 0).

Матрица состояний линеаризованной системы:

ХП: в точке (1, 0, 0)

Корни: устойчивое положение равновесия

ХП: 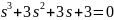в точке (4, 0, 0)

Корни: неустойчивое положение равновесия

Система устойчива «в малом».

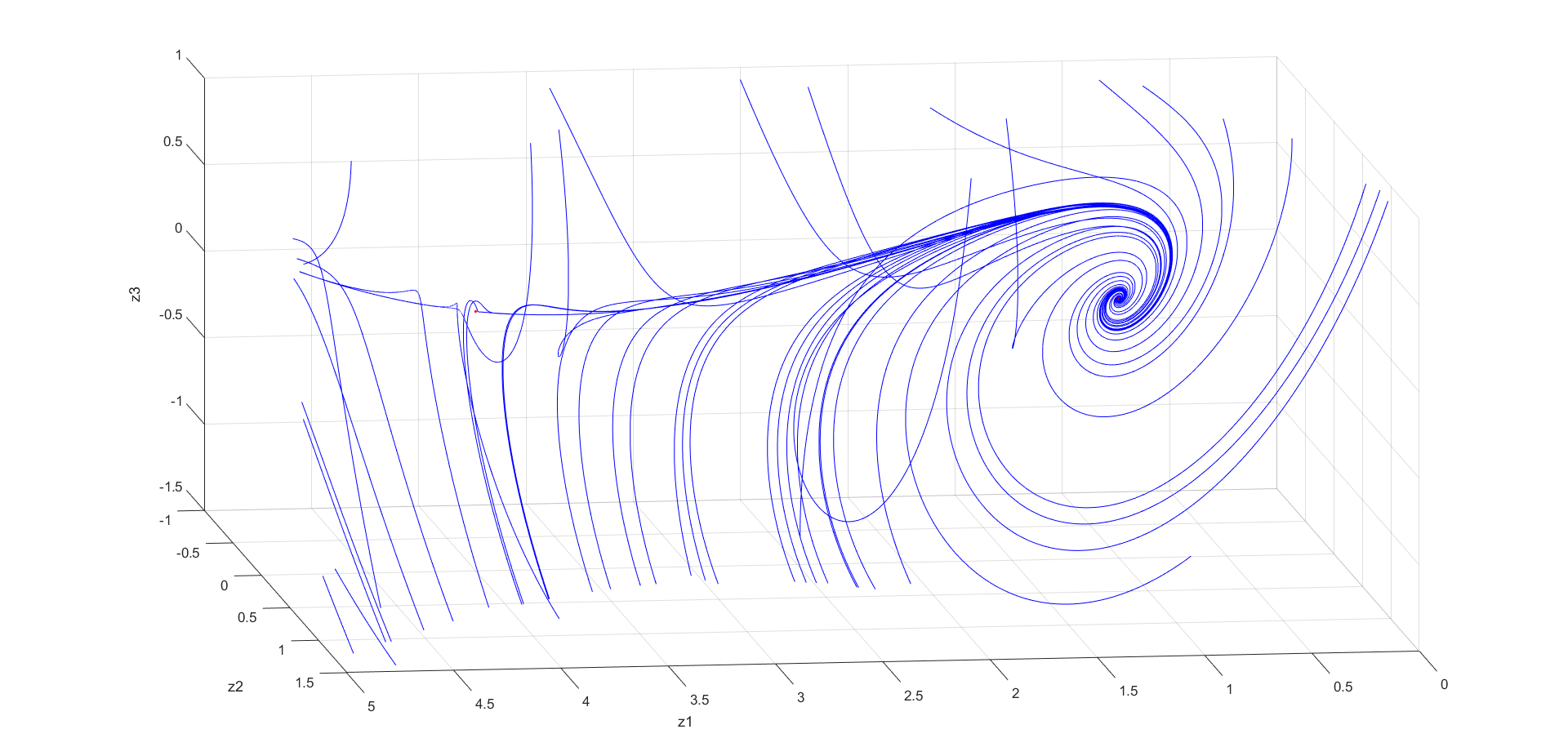
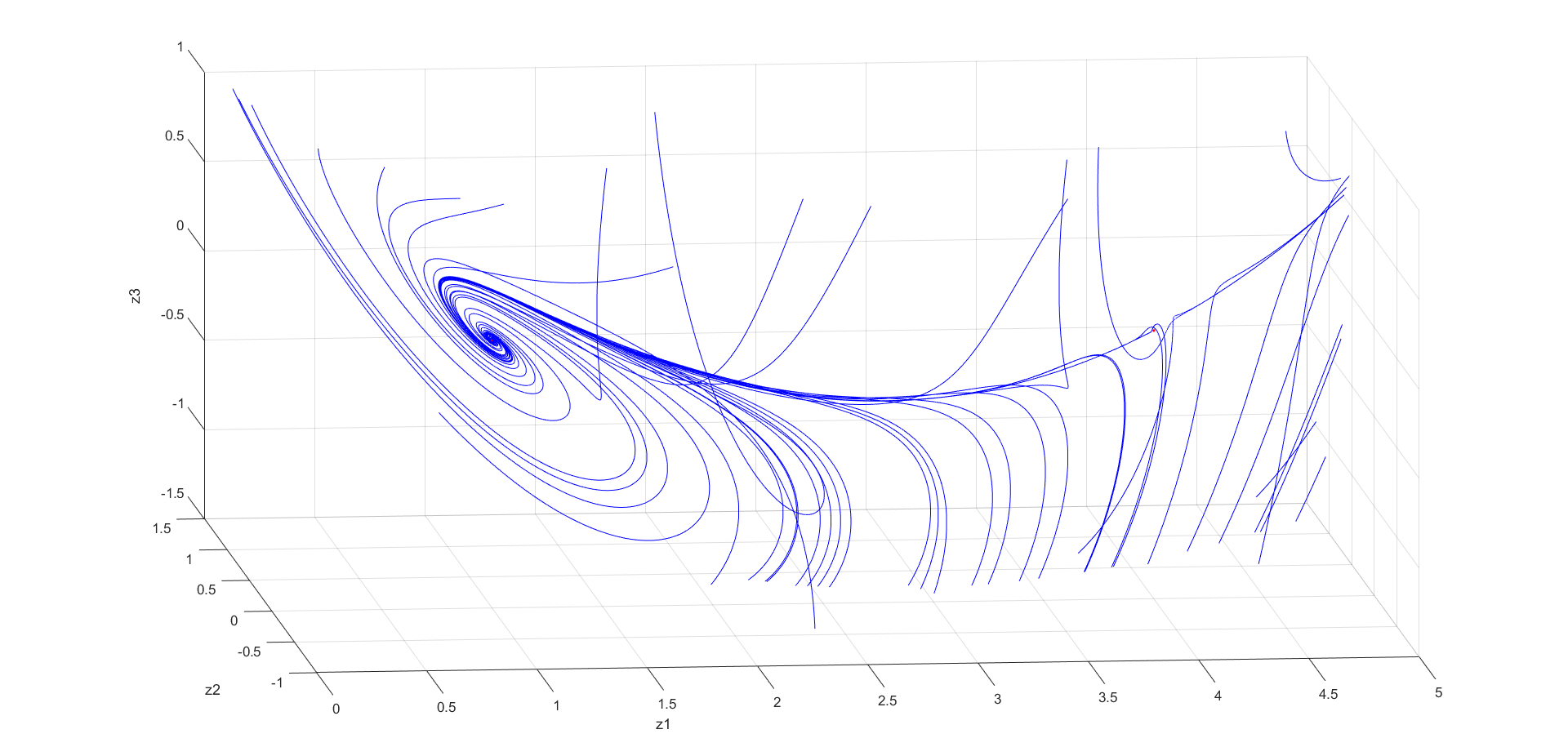
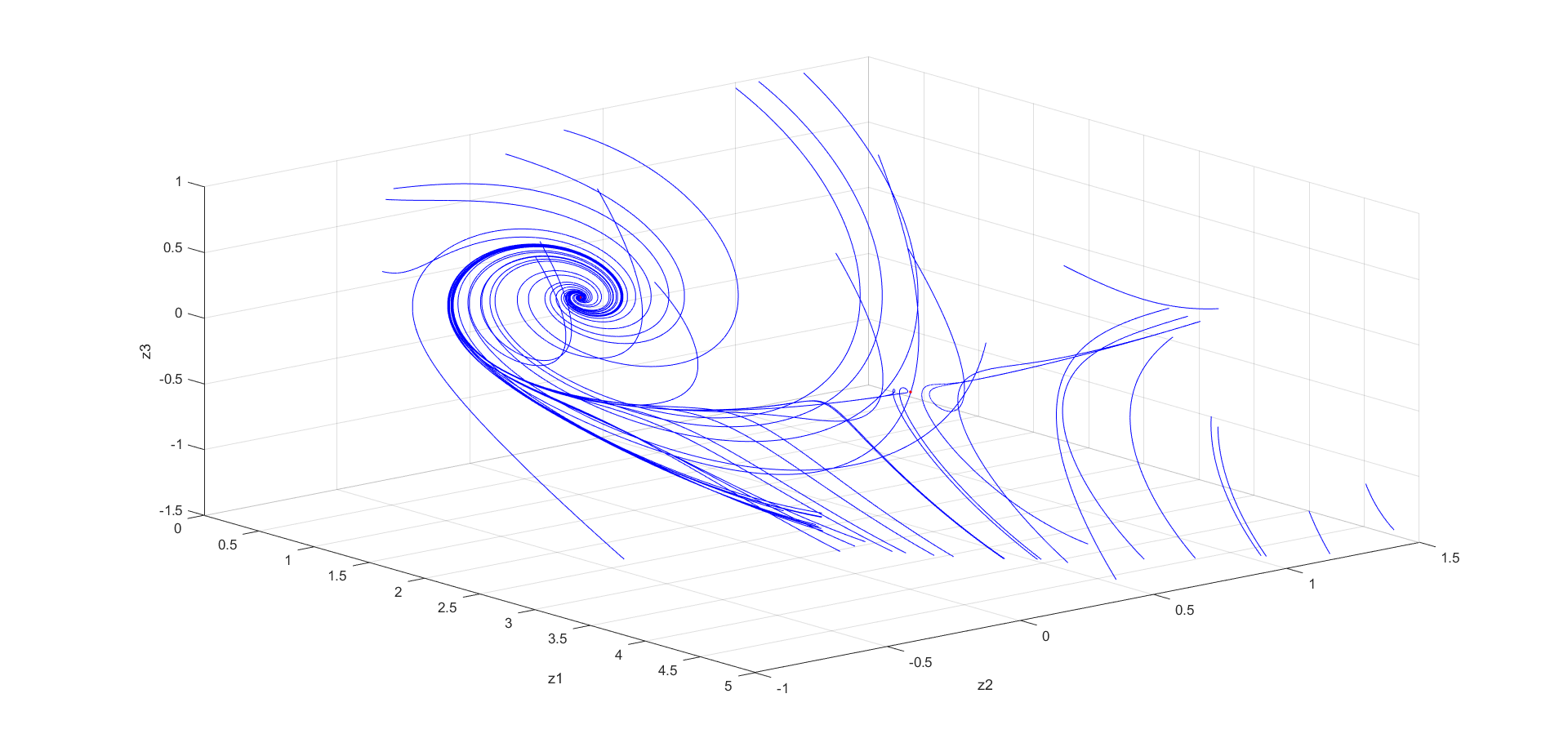
Рис. 3-5 Фазовый портрет системы

Цель работы.

Был произведен анализ устойчивости двух нелинейных систем первым и вторым методом Ляпунова.