МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В. И. Ульянова (Ленина)
Кафедра АПУ
отчет
по лабораторной работе №2
по дисциплине ТАУ
Тема: Логические алгоритмы управления
Студенты гр. 0392 |
|
Иванов С. К. |
|
|
Стаськова А. Р. |
|
|
Частухин А. Р. |
Преподаватель |
|
Жеронкин К. М. |
Санкт-Петербург
2023
Цель работы.
Изучение логических систем управления на примере модели реле с гистерезисом.
Выполнение работы.
Описание системы
Рассмотрим
систему, представленную на Рис. 1
Рис. 1 Принципиальная схема релейной системы стабилизации температуры
Датчик температуры
θ доставляет информацию о достижении
пороговых значений
,
и, тем самым, выделяет три ситуации
(события):
1
—
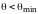(«Прохладно»);
2
—
(«Комфортно»);
3
—
(«Тепло»).
Управляющее воздействие
— напряжение, приложенное к нагревательному
элементу, может принимать два значения
0 В (выключен) и 220 В (включен).
Состояние температуры в доме может быть описано в виде системы ДУ в форме Коши:
Где
температура,
– мощность нагревателя (в нашем случае
принимает
значения из множества
),
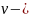не
интерпретируемая переменная. Тем не
менее, заметим, что при
то
есть
в
силу инертности системы. Параметры
системы установим
мин,
мин,
.
Исследуем систему на устойчивость.
Коэффициенты
разного знака, система неустойчива.
Регулятор может быть
описан в виде конечного автомата,
реализующего реле с гистерезисом (Рис.
2). В этом случае система становится
гибридной
(Рис. 3)
Рис. 2 СХ релейного регулятора
Рис. 3 Гибридная модель системы управления
Для реализации
автомата введем вектор событий
,
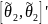введя следующие состояния:
– «прохладно»,
- «комфортно»,
- «тепло».
Выходом регулятора
будет состояние
принимающее
значение 0, если регулятор выключен и
1, если включен.
Функции перехода автомата будут выглядеть следующим образом:
Функции перехода автомата
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
Компьютерная модель.
В
результате моделирования системы
средствами Python
был получен график
(Рис. 4). Начальные условия приняты
нулевыми.
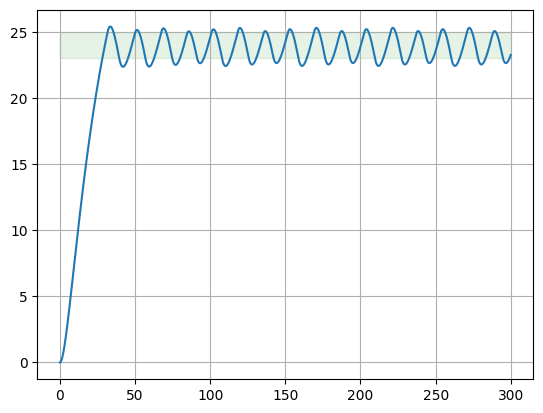
Рис. 4 Зависимость температуры от времени
Обращаем
внимание на колебания в зоне
.
Проведем более глубокий анализ графика.
Нас в первую очередь интересует амплитуда и период получившихся колебаний, поэтому будем анализировать установившуюся часть сигнала.
Для
того, чтобы найти параметры период
и амплитуду
будем применять преобразование Фурье,
поэтому сначала опустим синусоиду,
посредством вычитания из сигнала его
математического ожидания (Рис. 5)
Рис. 5 Частично нормированные данные
Теперь применяем преобразование Фурье:
spec = np.abs(np.fft.fft(period_try))
spec = 2/len(time_try)*spec
freqs = np.fft.fftfreq(period_try.shape[0], dt)
plt.grid()
plt.xlabel('Частота, Гц')
#plt.xlim(-10, 10)
plt.plot(freqs, spec)
plt.grid()
plt.xlim(-0.5, 0.5)
Спектр представлен на Рис. 6
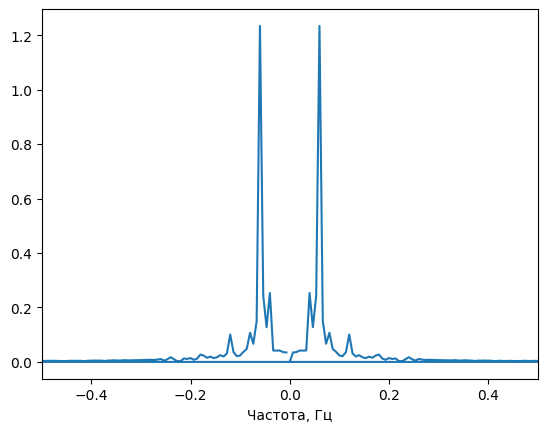
Рис. 6 Спектр сигнала
По спектру определяем частоту и амплитуду. Поскольку мы заранее «опустили» синусоиду, пик соответствует частоте сигнала.
f = freqs[np.argmax(spec)]
A = np.max(spec)
Получаем
,
Идеальное реле.
Заменим реле с гистерезисом на идеальное реле.
Это можно сделать двумя способами:
«Схлопнуть» гистерезис у уже существующей модели
Написать новый, но более простой автомат
Пойдем вторым путем.
def ode_sys_2_control(theta):
return int(theta < 22)
def ode_sys_2(x, t):
v, theta = x
u = 220 * ode_sys_2_control(theta)
dv_dt = (u - v)/T_1
dtheta_dt = (k*v - theta) / T_2
return (dv_dt, dtheta_dt)
Теперь, запустив модели, получаем принципиально другую картину:
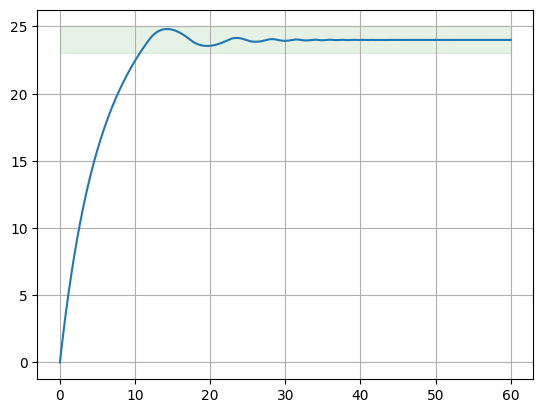
Рис. 7 График при использовании идеального реле
Здесь видим быстро затухающие колебания. Однако, кажущееся улучшение, относительно предыдущего результата, обманчиво. Поскольку амплитуда с каждым периодом экспоненциально падает (а модель поведения температуры остается той же), частота включения – выключения нагревателя неуклонно растет, что рано или поздно приведет к его отказу. Поэтому такой регулятор неприменим.
Этот факт может быть продемонстрирован следующим кодом:
x = sol_ode_sys_2[:,1]
peaks, _ = find_peaks(x, height=0)
plt.plot(x)
plt.plot(peaks, x[peaks], "x")
plt.grid()
plt.show()
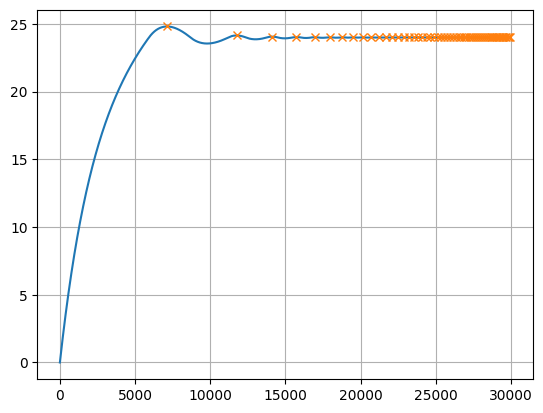
Рис. 8 Пики затухающей синусоиды
diff = [peaks[i + 1] - peaks[i] for i in range(len(peaks) - 2)]
plt.plot(diff)
plt.grid()
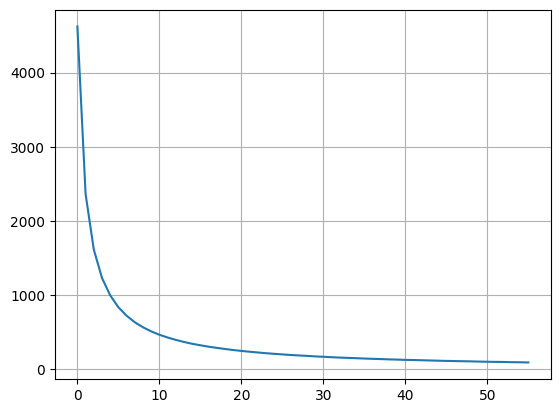
Рис. 9 Демонстрация убывания периода
Из Рис. 8 и Рис. 9 очевидно, что скорость переключения нагревателя растет со временем. В реальных системах это недопустимо.
Выводы
В результате работы были рассмотрены логические алгоритмы управления: регулятор, представленный в виде конечного автомата, реализующего реле с гистерезисом, конечный автомат, реализующий идеальный гистерезис.
В случае с идеальным реле можно достичь лучшего результата – колебания получаются затухающими, а температура оказывается в нужном промежутке.