
Задание 4
Для системы из задачи 3 определим установившуюся ошибку при экспоненциальном воздействии
1 |
|
|
|
|||
g(t) = e−αgt, G(s) = G(s) = |
|
. |
|
|||
s + αg |
|
|||||
Согласно варианту №5 αg = 0.8, значит воздействие примет вид |
|
|||||
1 |
|
|
|
|||
g(t) = e−0.8t, G(s) = G(s) = |
|
. |
(9) |
|||
s + 0.8 |
||||||
E(s) = Φeg(s)G(s) = |
s(s + 10)(3s + 10) |
(10) |
||||
|
||||||
(3s3 + 40s2 + 14100s + 140000)(s + 0.8) |
||||||
Для нахождение установившейся ошибки воспользуемся теоремой о конечном
значении оригинала во временной области: |
|
|
||||
|
|
|
|
s2(s + 10)(3s + 10) |
||
eg уст = lim e(t) = lim sE(s) = lim |
|
|
|
= 0. |
||
(3s3 |
+ 40s2 |
|
||||
t→∞ |
s→0 |
s→0 |
+ 14100s + 140000)(s + 0.8) |
|||
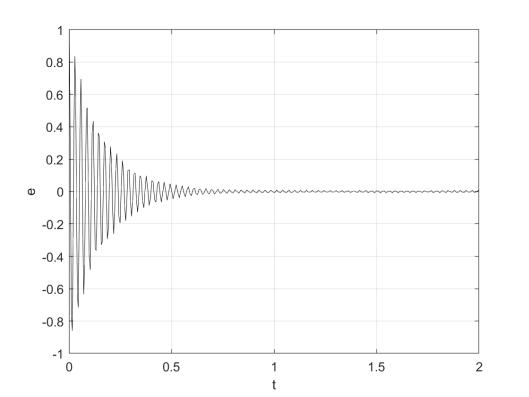
Рис. 12: Ошибка при экспоненциальном воздействии.
18
Ответы нв вопросы;
•Какой характер (монотонный, апериодический, колебательный) имеет реакция системы на выходе на такое воздействие? Подтвердить графиком процесса.
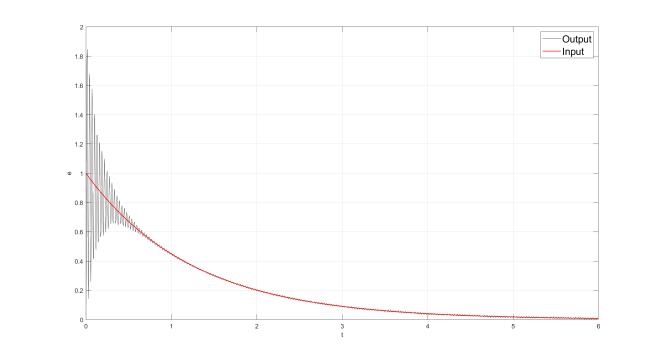
Ответ: реакция системы на выходе имеет колебательный характер, см. Рис 13.
Рис. 13: Реакция системы на экспоненциальное воздействие.
•Будет ли система селективно абсолютно инвариантна по ошибке к задающему воздействию? Можно ли в данной системе обеспечить указанное свойство? Если да, то какие изменение в системе следует произвести (со-
храняя при этом структуру операторов звеньев W0(s), Wp(s), но не ограничивая структуру системы), чтобы обеспечить указанное свойство? Ответ: Система при заданных параметрах не является абсолютно инвариантной по ошибке к задающему воздействию, что видно из (10) – полюс
sg = −0.8 не является нулём ПФ контура по ошибке Φeg(s).
Однако, меняя параметры регулятора, добиться этого свойства можно. Для этого воспользуемся выражением (8): числитель должен быть равен нулю на спектре воздействия, то есть
(0.8T1 − 1)(0.8T2 − 1) = 0,
T1 = 1.25, T2 = 1.25.
19

•Какой будет величина установившейся ошибки, если регулятор реализует
П-закон, т. е. Wr(s) = kr? Ответ: Если Wr(s) = kr, то
14kr
Wp(s) = W0(s)Wr(s) = (0.1s + 1)(0.3s + 1),
Φeg(s) = |
1 |
|
= |
(s + 10)(3s + 10) |
, |
(11) |
|
|
|
||||
1 + Wp(s) |
3s2 + 40s + 100 + 1400kr |
|||||
eg уcт(s) = lim s Φeg(s) G(s) = 0.
s→0
20

Задание 5
Определим установившуюся ошибку в системе и ответим на поставленные в задаче 4 вопросы, рассматривая вместо задающего возмущающее воздействие вида
1 |
|
|
|
||
f(t) = 1 − e−αf t, F (s) = |
|
|
|
|
|
s(s + αf ) |
|
||||
при использовании П- и ПИ-регулятора. kr = 100. |
|
||||
Согласно варианту №5 αg = 0.6, тогда |
|
||||
1 |
|
|
|
||
f(t) = 1 − e−0.6t, F (s) = |
|
|
(12) |
||
s(s + 0.6) |
|||||
.
•Для расчета ошибки при использовании П-регулятора воспользуемся выражением (11), учитывая изменение знака (пoскольку теперь рассматривается возмущение):
e |
lim s |
(s + 10)(3s + 10) 1 |
|
|
= − |
5 |
0.0165. |
|||||
|
|
|
|
|
|
|||||||
3s2 + 40s + 10100 s(s + |
0.6) |
303 |
||||||||||
|
f уст = − s |
→ |
0 |
≈ − |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
Замечание 1: ошибка при заданной топологии не зависит от параметров
звеньев и равна ef уст = −α (k1 +1).
g r
• Ошибку при ПИрегулировании рассчитаем, используя (8):
e |
lim s Φ |
eg |
F (s) = |
lim |
Φeg(s) |
|
= 0, |
|||||
s + 0.6 |
||||||||||||
|
f уст = − s |
→ |
0 |
|
− s |
→ |
0 |
|
||||
|
|
|
|
|
|
|
|
|
|
|||
поскольку Φeg(0) = 0.
Ответы на вопросы:
•Какой характер (монотонный, апериодический, колебательный) имеет реакция системы на выходе на такое воздействие? Подтвердить графиком процесса.
Ответ: При обоих видах регулирования на выходе наблюдается колебательный характер реакции (Рис. 14).
•Будет ли система селективно абсолютно инвариантна по ошибке к задающему воздействию? Можно ли в данной системе обеспечить указанное свойство?
Ответ: Система не будет селективно абсолютно инвариантна к задающему воздействию по той же причине, что и в предыдущем задании. Обеспечить селективную абсолютную инвариантность к данному воздействию можно тем же методом. Полюсы воздействия s1 = 0, s2 = −0.6.
21
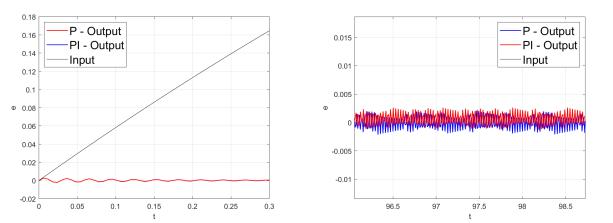
(a) Реакция системы. |
(b) Сравнение реакций. |
Рис. 14: Реакция системы.
a. При П-регулировнии невозможно:
DΦeg = (T1s + 1)(T2s + 1) ̸= 1 при s = 0.
b. При ПИ-регулировнии:
DΦeg = s(T1s + 1)(T2s + 1) = 0
на спектре возмущения только тогда, когда
T1 = 5/3, T2 = 5/3.
22
