

Задание 3
Для той же системы с ПИ-регулятором (см. ПФ Wr(s) в задаче 2) и ПФ объекта:
W0(s) = |
k0 |
|
, Wr(s) = kr |
Tиs + 1 |
(6) |
|
|
|
|
|
|||
(T1s + 1)(T2s + 1) |
s |
|||||
Приняты kr = 100, Tи = 1.
Значения постоянных времени T1 = 0.1, T2 = 0.3 и k0 = 14 (согласно варианту №5). Тогда
1400 (s + 1) |
|
Wp(s) = s(0.1s + 1)(0.3s + 1). |
(7) |
1.Определим диапазоны частот Ω1 и Ω2 задающего гармонического воздействия g(t) = Ag sin(ω0t), для которых относительная амплитуда устано-
вившейся ошибки Ag |
≤ 0.01 и Ag |
≈ 1. |
Ae |
Ae |
|
Для установления диапазонов воспользуемся ЛАЧХ разомкнутого контура 20 lg |Wp(jω)| (Рис. 7), имея в виду, что
1
|Φeg(jω)| = |1 + Wp(jω)|.
•При значительном усилении разомкнутого контура, единицей в знаменателе можно пренебречь, получив выражение
Ag |
= |
1 |
|
≤ 0.01, |
Ae |
|Wp(jω)| |
|||
откуда |Wp(jω)| ≥ 100. Поскольку проще работать с ЛАЧХ, это условие стоит интерпретировать как требование
Lp(ω) ≥ 20 lg(100) = 40 дБ. |
( ) |
Частоты, удовлетворяющие этому условию, образуют искомый диапазон Ω1 (Рис. 7, зеленая часть АЛАЧХ графика)
•При усилении меньше −20 дБ напротив, можно пренебречь Wp(jω). Тогда
Ag ≈ 1,
Ae
А значит услоие для ЛАЧХ имеет вид |
|
Lp(ω) ≤ −20 дБ. |
( ) |
Частоты, удовлетворяющие этому условию, образуют искомый диапазон Ω2 (Рис. 7, красная часть АЛАЧХ).
12
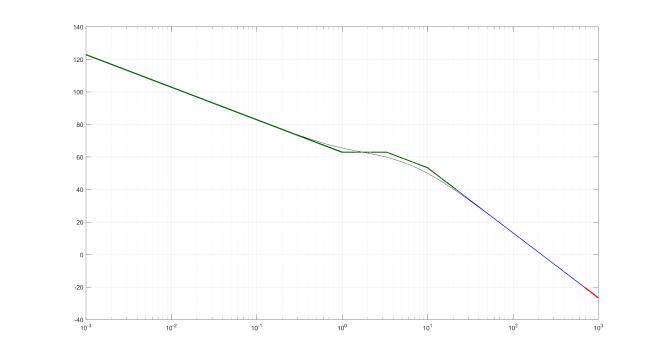
Рис. 7: ЛАЧХ разомкнутого контура.
Из графика получаем ответ:
Ω1 = (0, 20] Гц Ω2 = [683, +∞) Гц
2.Определм абсолютные значения амплитуды ошибки Ae для двух значений частоты ω0 воздействия в каждом из диапазонов, при Ag = 1. Проведем вычислительные эксперименты, подав на вход системы гармонические сигналы соответствующих частот и построим графики временных процессов.
Для начала найдем ответ аналитически.
|
|
Ae(ω) = |Φeg(jω)| = |
|
1 |
|
|
= |
|
|
|
1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
1 + W |
(jω) |
| |
|
|
1400(jω+1) |
|
|
||||||
Возьмем частоты |
|
| |
p |
|
|
1 + jω(0.1jω+1)(0.3jω+1) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ω11 |
= 5 |
рад, ω12 = 15 |
рад для диапазона Ω1 |
|
|
|
|
|
||||||||
|
|
с |
с |
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω21 |
= 800 рад, ω22 = 1000 рад для Ω2. |
|
|
|
|
|
|
|
|
|
||||||
|
|
с |
|
с |
|
|
|
|
|
|
|
|
|
|
|
|
Подставляя, получаем |
|
|
|
|
(Ae(ω21) |
|
|
|
|
|
||||||
|
|
Ω1 (Ae(ω12) |
≈ |
0.008 < 0.01. |
Ω2 |
≈ |
0.999 |
≈ |
1. |
|
||||||
|
|
Ae(ω11) |
≈ |
0.002 < 0.01, |
|
|
Ae(ω21) |
≈ |
0.997 |
≈ |
1, |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
13
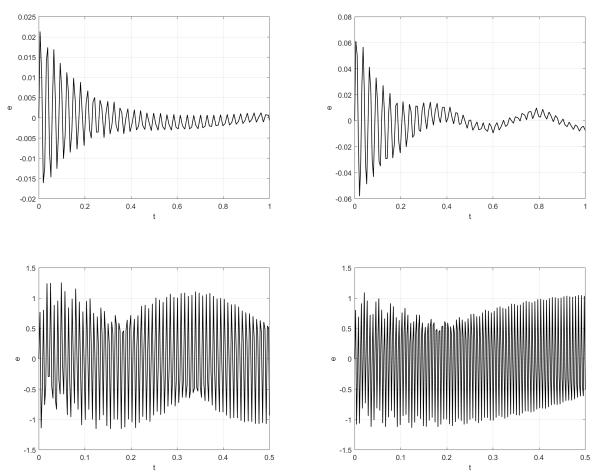
(a) ω11 |
(b) ω12 |
(c) ω21 |
(d) ω22 |
Рис. 8: Переходные процессы.
Проверим результаты с помощью Matlab. На Рис. 8 приведены графики переходных процессов, на Рис. 9 – результаты прохождения синусоид заданных частот через систему. Медианное значение амплитуды ошибки в результате эксперимента:
Ω1 |
(Ae(ω12) |
≈ |
0.0067. |
Ω2 |
(Ae(ω21) |
≈ |
0.9641. |
|
Ae(ω11) |
≈ |
0.0013, |
|
Ae(ω21) |
≈ |
0.9433, |
|
|
|
|
|
|
14
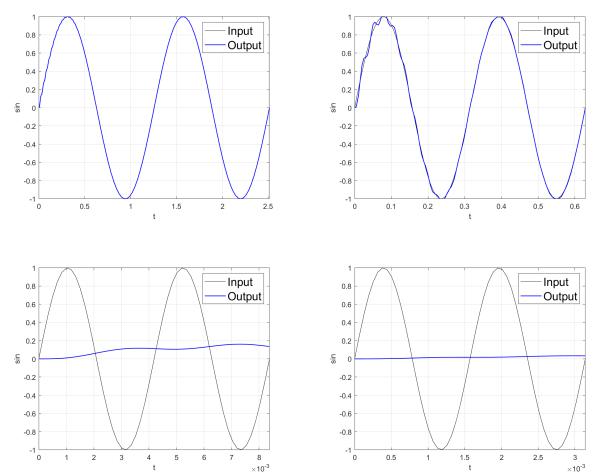
(a) ω11 |
(b) ω12 |
(c) ω21 |
(d) ω22 |
Рис. 9: Вход - выход.
Ответы на вопросы:
•Какой вид имеют АЧХ и ЛАЧХ замкнутой системы по ошибке Ответ: Построим график АЧХ и ЛАЧХ системы по ошибке, используя средства MATLAB (Рис. 10).
•Как изменятся рассчитанные диапазоны частот Ω1 и Ω2 при увеличении
(уменьшении) kr в 10 раз?
Ответ: При увеличении (уменьшении) kr в 10 раз график ЛАЧХ разомкнутого контура поднимется (опустится) на 20 log10 10 = 20 Дб. Значит определить новые диапазоны можно по исходному графику, увеличив (уменьшив) правую границу ( ) и левую границу ( ) на 20 Дб. Новые границы, полученные таким образом для увеличения и уменьшения kr соответственно:
Ω1 = (0, 68] Гц, Ω2 = [2160, +∞) Гц
и
Ω1 = (0, 3.25] Гц, Ω2 = [216, +∞) Гц.
15
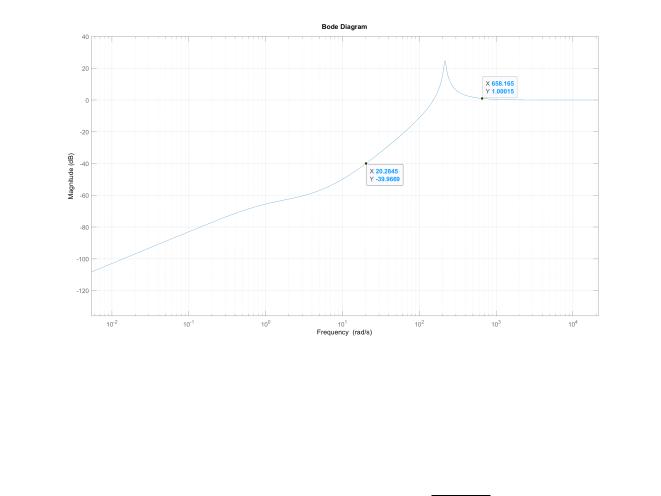
Рис. 10: ЛАЧХ замкнутого контура по ошибке
•Можно ли в данной системе обеспечить селективную абсолютную инвариантность по ошибке при гармоническом воздействии:
Ag ω0 g(t) = Ag sin ω0t, G(t) = s2 + ω02
где Ag – произвольная амплитуда, ω0 Ω1 – произвольная частота из найденного диапазона? Если да, то, какие изменения в системе следует произвести (сохраняя при этом структуру операторов звеньев Wo(s), Wp(s), но не ограничивая структуру (топологию) системы), чтобы обеспечить указанное свойство? Результаты подтвердить графиками.
Ответ: Для селективной абсолютной инвариантности по ошибке необходимо, чтобы ошибка Φeg(sj) = 0 на спектре sj воздействия g(t).
То есть в составе нулей передаточной функции Φeg(s) должны быть все полюса изображения воздействия g(t). Найдем точное выражение для Φeg (пока не меняем топологию системы), воспользовавшись (6):
Φeg(s) = |
1 |
|
= |
|
s(T1s + 1)(T2s + 1) |
(8) |
1 + Wp(s) |
T1T2s3 + (T1 + T1)s2 + (k0krTи)s + k0kr |
|||||
Полюса заданного воздействия s1, 2 = ±jω0, они должны входить в число корней числителя дроби (8). Для нахождения таких параметров T1 и T2 необходимо решить систему
(
jω0(jω0T1 + 1)(jω0T2 + 1) = 0,
−jω0(jω0T1 − 1)(jω0T2 − 1) = 0.
16
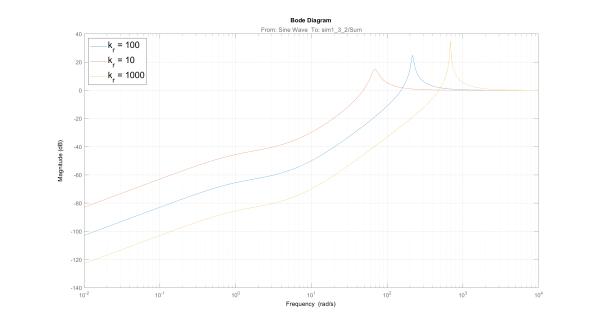
Рис. 11: ЛАЧХ при различных kr.
относительно T1 и T2, которая не имеет действительных решений. Значит обеспечить селективную инвариантность к данному типу воздействий, не изменяя топологию системы, невозможно.
17
