
Задание 2
Теперь для системы со струкрурной схемой на Рис. 1 примем
W0(s) = |
k0 |
, Wr(s) = kr |
Tиs + 1 |
, |
|
s(T0s + 1) |
|
s |
|||
cогласно варианту №5: k0 = 2, T0 = 1.
Определим условия параметрической настройки регулятора (коэффициент передачи kr и постоянную времени изодрома Tи), обеспечивающие устойчивость замкнутой системы.
Для это сначала найдем ПФ разомкнутой системы. |
|
||||||
|
Gp(s) |
|
2kr (Tиs + 1) |
|
|||
Wp(s) = |
|
|
= |
|
|
. |
(3) |
Dp(s) |
s2 (s + 1) |
||||||
Далее используем критерий Гурвица (необходимые условия выполнены при положительных параметрах звеньев)
D(s) = Dp(s)Gp(s) = s3 + s2 + 2krTиs + 2kr.
Для устойчивости необходимо и достаточно выполнения
∆ = 2krTи − 2kr = 2kr(Tи − 1) > 0. |
(4) |
Значит на параметры накладываются ограничения kr > 0; Tи > 1.
Построим зависимость установившейся ошибки при параболическом воздей-
ствии g(t) = |
g0 |
t2 = 0.5t2 от коэффициента kr. |
|
|
|||||
2 |
|
|
|||||||
1 |
Wp (s) = |
1 2kr (Tиs + 1) |
|||||||
|
|
Wp(s) = |
|
|
|
|
|
, |
|
|
|
|
s2 |
|
|||||
|
|
sν |
|
s + 1 |
|||||
k = Wp (0) = 2kr.
Степень астатизма системы ν = 2, степень воздействия l = 2 – астатическая система. Для нее
eg уст = |
g0 |
= |
|
1 |
= |
1 |
k |
|
2kr |
||||
|
|
2kr |
||||
– с увеличением kr установившаяся ошибка уменьшается по гиперболе (см. Рис. 2). Критический коэффициент устойчивости для системы
kr кр = 0,
что следует из выражения (4) для определителя Гурвица. Увеличение коэффициента делает систему устойчивой, уменьшение нарушает необходимое условие устойчивости.
8
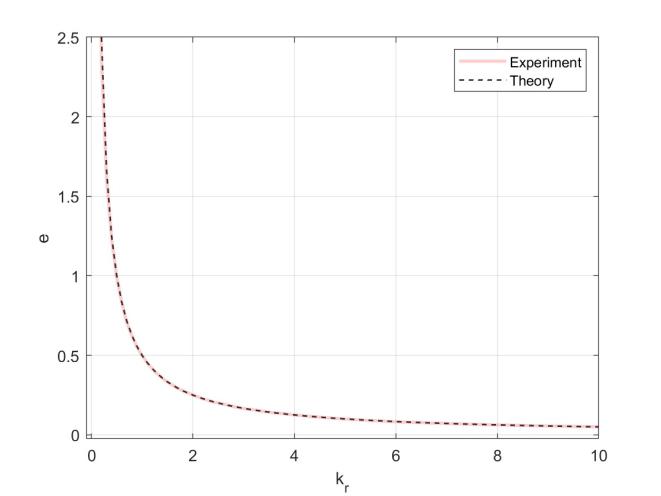
Рис. 4: Зависимость e(kr).
Ответы на вопросы:
•Какое минимальное значение установившейся ошибки при заданном воз-
действии можно обеспечить в этой системе за счёт Wr(s) регулятора? Ответ: Увеличение kr ведет к уменьшению ошибки. При kr → ∞, eg уст →
0.
•Показать, как изменяется характер (монотонный, апериодический, колебательный) переходного процесса в системе на воздействие вида g(t) =
0.5t2 при возрастании коэффициента kr, начиная с некоторого выбранного значения (выбор значений определяется требованием изменчивости характера процессов)? Ответ сопроводить графиками.
Ответ: Характер переходных процессов зависит не только от kr, но и от Tи. Проанализируем систему при Tи = 14.5 (из тех соображений, что при Tи = 14.5 и kr = 0.01 корни характеристического полинома замкнутой системы будут действительными, а знчит, ожидается монотонный переходный процесс).
Заметим, что при kr = 0 реакция будет расходящейся апериодической:
9
E(s) = |
1 |
L {g(t)} |
= |
|
s + 1 |
|
|
, |
(5) |
|||
|
|
|
|
|
|
|||||||
1 + Wp(s) |
s(s3 + s2 + 2Tиkrs + 2kr) |
|||||||||||
e0(s) = L−1 |
s + 1 |
|
= L−1 |
1 |
= |
t2 |
|
|
||||
|
|
. |
|
|
||||||||
s(s3 + s2) |
s2 |
2 |
|
|
||||||||
Второй предельный случай kr → ∞ см. в ответе на первый вопрос.
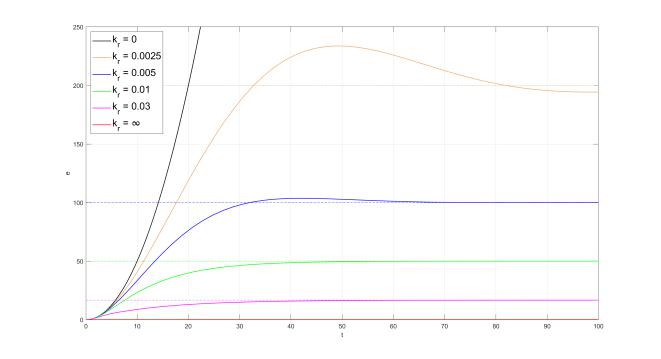
Для выбранного Tи, строго монтонный процесс при kr = 0.01, соответсвенно, уменьшая kr от 0.01 − ε до 0 + ε получим сначала апериодический, а затем колебательный процессы.
Рис. 5: Вид переходных процессов при различных kr.
•Каким будет установившийся режим в системе при выборе Tи = T0 kr = k0−1? Дать необходимые пояснения, привести график.
Ответ: подставляя Tи = 1 и kr = 0.5 в (4) имеем
∆ = 2kr(Tи − 1) = 0.
Следовательно, система находится на границе устойчивости.
Из (5) : |
|
|
|
|
||
E(s) = |
s + 1 |
= |
|
1 |
, |
|
|
|
|
||||
s(s3 + s2 + s + 1) |
s(s + i)(s − i) |
|||||
e(t) = L−1 {E(s)} = XRes |
E(s)est |
= 1 − cos(t). |
||||
|
|
|
|
|
||
То есть получаем незатухающие колебания относительно единицы. 10
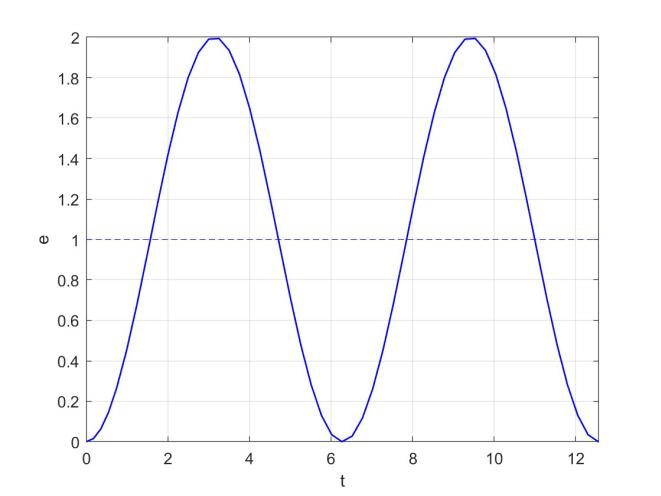
Рис. 6: kr = k0−1, Tи = T0.
11
