
МИНОБРНАУКИ РОССИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)
Факультет КТИ
Кафедра Автоматики и процессов управления
ОТЧЁТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №1
По дисциплине «Теория автоматического управления»
Вариант 5
Выполнил студент:
Иванов С. К. группа 0392
Проверил:
д.т.н., проф. Душин С. Е.
Санкт-Петербург, 2022.
Содержание
Лабораторная работа №1 |
3 |
Цель работы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
3 |
Задание 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
4 |
Задание 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
8 |
Задание 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
12 |
Задание 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
18 |
Задание 5 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
21 |
Задание 6 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
23 |
Вывод . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
25 |
2
Исследование типовых установившихся режимов систем автоматического регулирования.
Цель работы
Исследование типовых установившихся режимов систем автоматического регулирования (САР). Определение установившихся ошибок систем с обратной связью при степенных и гармонических воздействиях.
3
Задание 1
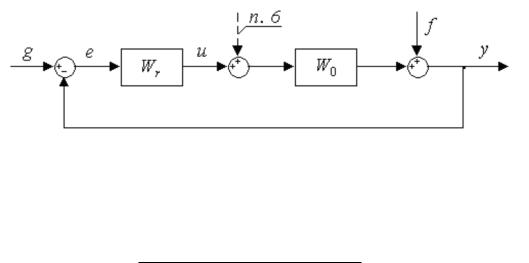
Рис. 1: Структурная схема.
Для структурной схемы на Рис.1 примем
k0
W0(s) = (T1s + 1)(T2s + 1)(T3s + 1), Wr(s) = kr
согласно варианту №5: T1 = 0.02, T1 = 0.8, T3 = 1.4, kr = 4.
Wp(s) = Wr(s)W0(s) = |
38 |
. |
(1) |
|
|||
(0.02s + 1)(0.8s + 1)(1.4s + 1) |
Определим ошибки при ступенчатом и линойном воздействиях.
Заметим, что степень астатизма данной системы ν = 0, поскольку в системе нет интеграторов. Тогда Wp (s) = Wp(s).
eg уст = lim |
sν−l |
|
, |
(2) |
||
|
|
|||||
s |
→ |
0 sν + W |
(s) |
|
||
|
|
p |
|
|||
где ν – степень астатизма системы, а l – степень воздействия.
1.Ступенчатое возмущающее воздействие f(t) = f01(t), f0 = 1
ν = l = 0 – статическая система. Поскольку рассматриваем ошибку по возмущению, в выражении (2) изменится знак
e |
lim |
|
1 |
|
1 |
|
. . |
|||
|
|
|
|
|
|
|||||
|
38 |
|
|
|
|
|||||
|
f уст = − s |
→ |
0 |
1 + |
|
= −39 ≈ −0 |
0256 |
|||
|
(0.02s+1)(0.8s+1)(1.4s+1) |
|
||||||||
|
|
|
|
|
|
|
||||
2.Линейное воздействие g(t) = g0t, g0 = 1. ν < l, а значит eg уст → ∞.
4
Ответы на вопросы:
•Система статическая или астатическая?
Ответ: система статическая (порядок астатизма ν = 0).
•Какие параметры ПФ Wp(s) определяют величину установившейся ошибки по возмущению?
Ответ: На величину установившейся ошибки влияет kr – увеличение kr ведет к уменьшению ошибки.
•В чём заключается противоречивость требований к малости установившейся и переходной составляющих ошибки системы?
Ответ: Уменьшение установившейся составляющей ведет к увеличению колебательности контура, следовательно, время установления стремится к бесконечности, при стремлении установившейся составляющей к нулю.
•Какое минимальное значение установившейся ошибки по возмущению за-
данного вида можно обеспечить в этой системе за счёт kr регулятора? Увеличение kr до бесконечности невозможно, поскольку система потеряет устойчивость. Найдем kr кр, используя критерий устойчивости Гурвица.
D(s) = Dp(s) + Gp(s) = 0.0224s3 + 1.164s2 + 2.22s + (1 + 9.5kr кр),
где 9.5kr кр - критический коэффициент устойчивости.
∆ = d2 d1 − d3 d0 = 1.164 · 2.22 − 0.0224 · (1 + 9.5kr кр) = 0.
Откуда |
32021 |
|
|
|
||||
|
|
|
|
|
||||
kr кр = |
|
|
≈ 12.037 |
|
||||
|
2660 |
|
||||||
Причем ошибка, которая достигается в этом случае |
||||||||
1 |
|
|
1000 |
|
|
|||
eg уст min = − |
|
= − |
|
|
≈ −0.009. |
|||
1 + kr кр k0 |
115361 |
|||||||
Ответ: eg уст min ≈ −0.009.
5
Подтвердим последний пункт экспериментально.
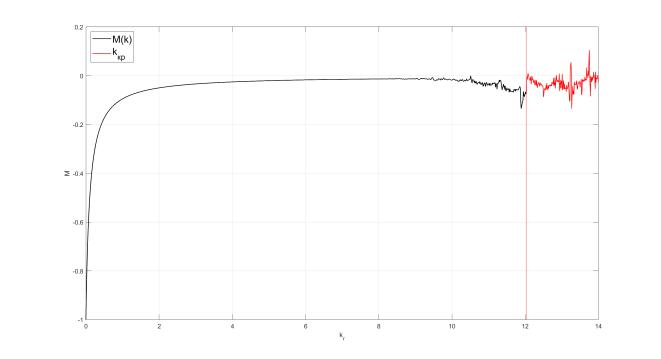
Поскольку характер переходного процесса для данных параметров колебательный, при достаточном времени наблюдения установившейся ошибкой можно считать медиану выборки, полученной симуляцией системы. Будем перебирать параметр kr от 0 до 14 и построим график зависимости медианы M от kr, см. Рис. 2.
Рис. 2: Установившаяся ошибка системы при различных kr
При kr, достаточно близком к kr кр слева, процесс становится сильно колебательным Рис. 3 (b), а значит время, необходимое для установления ty → ∞ и оценка установившейся составляющей через медиану может быть некорректной. При kr > kr кр ≈ 12 происходит потеря устойчивости, процесс становится колебательным расходящимся Рис. 3 (d). Поэтому на графике в районе kr кр видны скачки, а при kr > kr кр результат не интерпретируем.
6
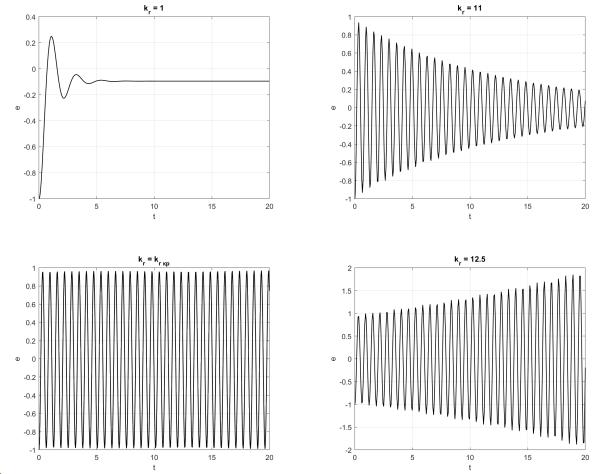
(a) |
(b) |
(c) |
(d) |
Рис. 3: Переходные процессы.
7
