
МИНОБРНАУКИ РОССИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА)
Факультет КТИ
Кафедра Автоматики и процессов управления
ОТЧЁТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №2
По дисциплине «Теория автоматического управления»
Вариант 5
Выполнил студент:
Иванов С. К. группа 0392
Проверил:
д.т.н., проф. Душин С. Е.
Санкт-Петербург, 2022.
Содержание
Лабораторная работа №1 |
3 |
Цель работы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
3 |
Задание 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
4 |
Задание 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
14 |
Задание 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
16 |
Выводы. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
19 |
Приложения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
20 |
2
Aнализ качества переходных процессов в системах автоматического регулирования.
Цель работы
Анализ качества переходных процессов в системах автоматического регулирования. Определение прямых и косвенных показателей качества.
3
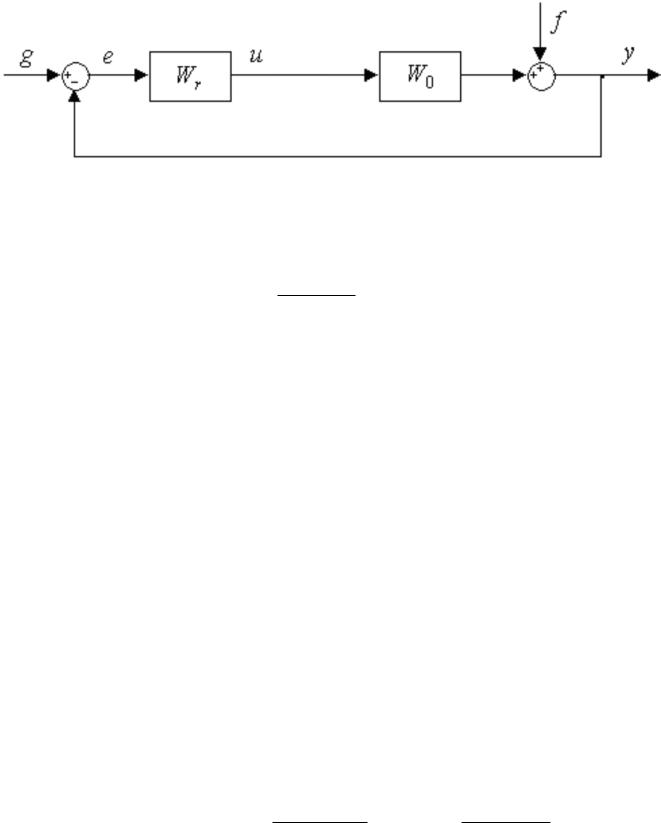
Задание 1
Рис. 1: Структурная схема.
Для системы автоматического регулирования, структурная схема которой приведена на Рис. 1, принято:
1
W0(s) = s(T s + 1), Wr(s) = kr
Согласто варианту №5: T = 1.1. |
|
||
Тогда |
|
||
|
kr |
|
|
Wp = |
|
. |
(1) |
s(1.1s + 1) |
|||
•Построим корневой годограф при изменении kr т нуля до бесконечности. Результат построения приведен на Рис. 2.
1 |
T = 1 |
. 1 ; |
2 |
sys = |
t f ( [ 1 ] , [T 1 0 ] ) ; |
3 |
r l o c u s ( sys ) |
|
4 |
grid on ; |
|
|
|
|
•Найдем аналитические зависимости косвенных показателей качества µ и η от значения коэффициента передачи kr.
Разрешим уравнение, полученное путем приравнивания к нулю характеристического полинома замкнутой системы:
D(s) = Dp(s) + Gp(s) = T s2 + s + kr = 0.
Решая уравнение в общем виде получаем |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
√ |
|
|
s |
|
= |
− |
1 |
± |
1 − 4 T kr |
|
= |
− |
|
1 |
± |
1 − 4.4kr |
. |
|||
1,2 |
2 T |
|
|
2.2 |
|
||||||||||||
|
|
|
2T |
|
|
|
2.2 |
|
|||||||||
По определению |
|
|
|
µ = maxi |
Re(si) |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
Im(si) |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4
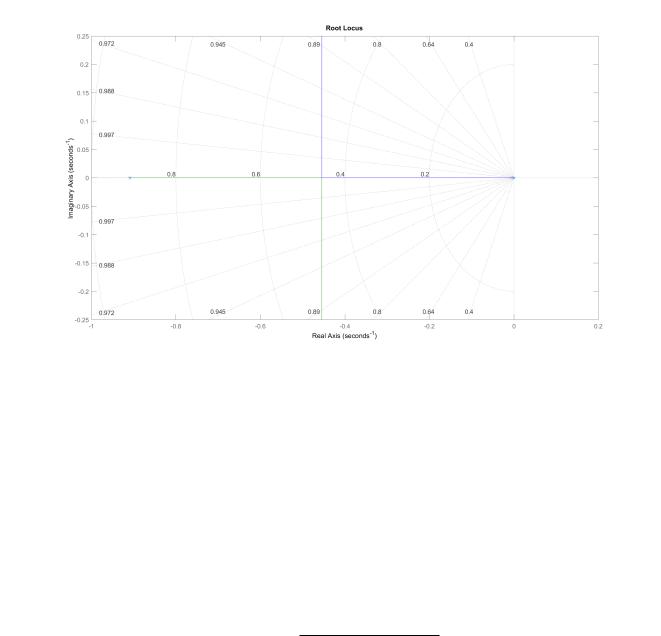
|
|
|
|
|
Рис. 2: Корневой годограф. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
При kr ≤ |
5 |
|
оба корня чисто действительные, а значит µ = 0. При kr > |
5 |
|
||||||||||||||||||||||||||||||||||||
22 |
22 |
||||||||||||||||||||||||||||||||||||||||
имеем |
|
|
|
|
|
p |
|
|
|
|
|
|
|
p |
|
|
|
|
|
|
= |
|
p |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
µ = max |
4.4 kr |
− 1 |
, − |
4.4 kr − 1 |
|
4.4 kr − 1 |
. |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
По определению |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
η = mini |
|Re(si)| , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
При kr ≤ |
5 |
корни чисто действитальные, а значит |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
22 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
η = |
−1 + 1 − 4.4 kr |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Иначе – значение под корнем отрицательное, а значит η = |
1 |
|
|
= |
|
5 |
. Обо- |
||||||||||||||||||||||||||||||||||
2.2 |
11 |
||||||||||||||||||||||||||||||||||||||||
щая: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
(√4.4 kr |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
r |
|
|
1, kr |
> |
5 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
|
|
kr |
≤ |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
µ(k |
) = |
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
5 |
|
|
√ |
|
|
|
|
|
|
|
|
|
|
≤ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
η(kr) = |
|
|
|
2.2 |
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
(11 , |
|
|
|
|
|
|
|
|
|
kr > |
22 . |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
−1+ 1−4.4 kr |
|
, kr |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.Определим корневые показатели µ и η при нескольких значениях kr, взятых из интервала 0 < kr < 5000. Построим графики аналитических зависимостей показателей качества µ и η от kr. Здесь и далее: все рассчитанные
5
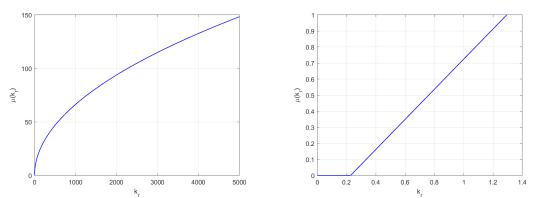
(a) |
(b) |
Рис. 3: µ(kr).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
значения занесены в таблицу Табл. 1. Графики зависимостей коэффициентов µ и η от kr см. на Рис. 3 и Рис. 4 соответственно.
%mu: |
|
|
|
|
|
N = 1000; |
|
|
|
||
k_r |
= |
l i n s p a c e (5/22 , 5000 , N) ; |
|||
mu = s q r t (4 T k_r − 1) ; |
|
||||
k_l |
= |
l i n s p a c e (0 , |
5/22 , |
N/100) ; |
|
mu_l = 0 k_l ; |
|
|
|||
plot (k_r , |
mu, ’ LineWidth ’ , 1) |
||||
hold |
on |
|
|
|
|
plot ( k_l , |
mu_l , ’ LineWidth ’ , 1) |
||||
grid |
on |
|
|
|
|
%eta : |
|
|
|
|
|
N = 500; |
|
|
|
||
k_r |
= |
l i n s p a c e (0 , |
5/22 , |
N) ; |
|
eta |
= |
abs((−1+ s q r t (1 − 4.4 k_r) ) /2 . 2 ) ; |
|||
k_l |
= |
l i n s p a c e (5/22 ,1 , |
N/100) ; |
||
eta_l |
= zeros (1 , |
N/100) |
+ 5/11; |
||
plot (k_r , |
eta , ’ LineWidth ’ , 1) ; |
||||
hold |
on |
|
|
|
|
plot ( k_l , |
eta_l , |
’ LineWidth ’ , 1) ; |
|||
grid |
on |
|
|
|
|
|
|
|
|
|
|
6
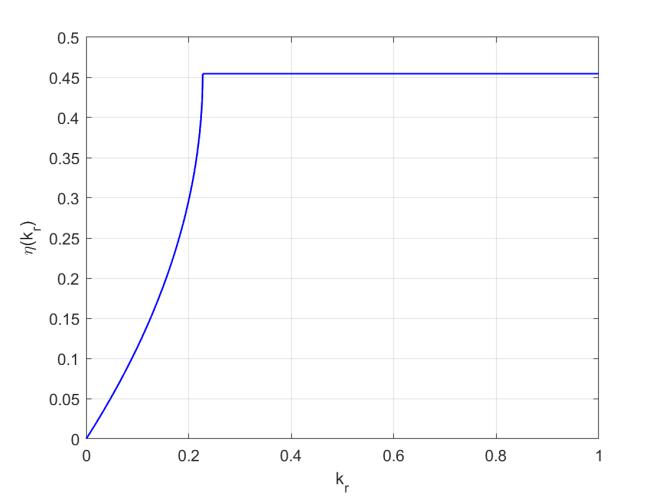
Рис. 4: η(kr).
2.Определим прямые показатели качества tp и σ% при нескольких значениях kr, построим графики. Воспользуемся теоремой о конечном значении оригинала для нахождения установившегося значения:
|
Wp(s) |
|
kr |
|
|
W (s) = |
|
= |
|
. |
(2) |
1 + Wp(s) |
T s2 + s + kr |
||||
Тогда
h |
lim s W (s)H(s) = lim s |
· |
kr |
· |
1 |
= |
kr |
= 1. |
|||
T s2 + s + kr |
|
|
|
|
|||||||
|
уст = s→0 |
s→0 |
|
s |
kr |
|
|||||
Теперь построим графики зависимостей tp(kr) и σ(kr) (Рис. 5 и Рис. 6 соотвественно). Вид переходного процесса при различных kr можно наблюдать на Рис. 7. Код к графикам в виду его громоздкости приведен в приложении 1.
7
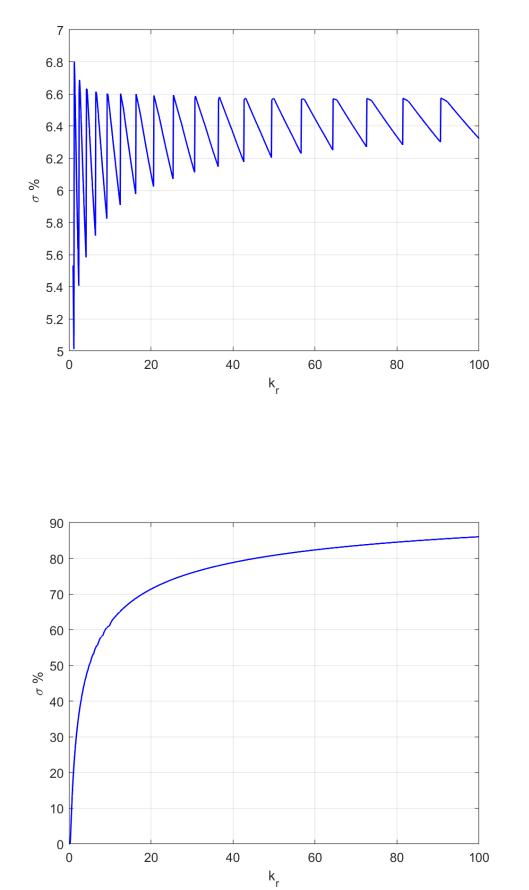
Рис. 5: tp(kr).
Рис. 6: σ(kr).
8
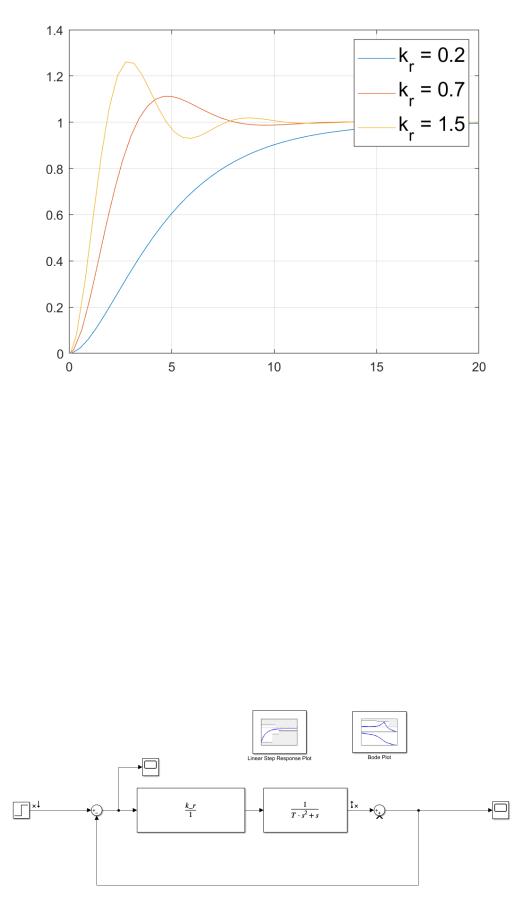
Рис. 7: Переходные процессы.
3.Определим частотные показатели качества ∆L, ∆φ и ωср по ЛЧХ разомкнутой системы Lp(ω), φp(ω) при значениях kr, приведенных в табл. 1.
Заметим, что поскольку разомкнутая система описывается одним инте-
гратором и одним апериодическим звеном, частота ωπ пересечения ФЧХ с прямой −π лежит в бесконечности, а значит запас устойчивости по амплитуде не ограничен.
Все зависимости построены с помощью Matlab, модель Simulik приведена ниже. Код см. в приложении 2.
Рис. 8: Используемая модель Simulink "sim1.slx".
9
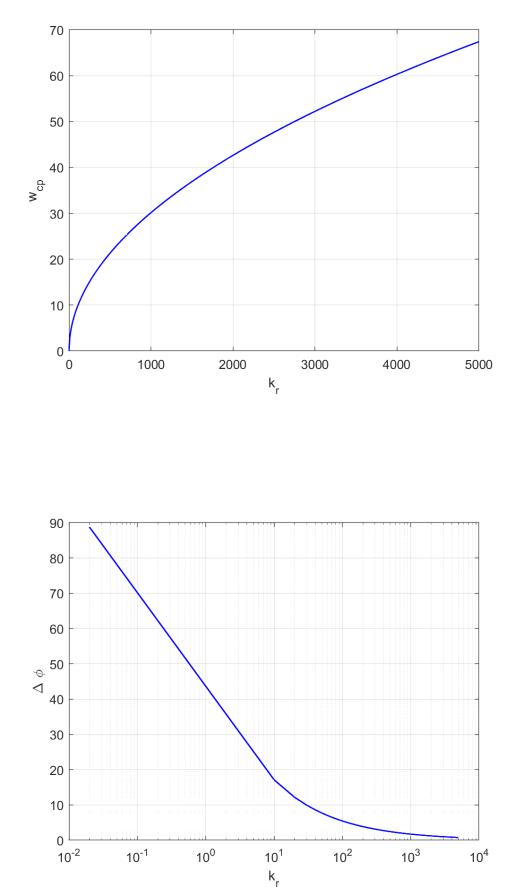
Рис. 9: Зависимость ωср(kr).
Рис. 10: Зависимость ∆φ(kr).
10
