
Часть II
.docxЧасть II
Тройные интегралы.
Вспомним,
как мы определили двойной интеграл:
объем под поверхностью, заданной
уравнением
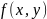 .
Тогда можно было бы сказать, что тройной
интеграл – гиперобъем «под» поверхностью
.
Тогда можно было бы сказать, что тройной
интеграл – гиперобъем «под» поверхностью
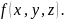 Однако, проще сделать несколько иначе.
Однако, проще сделать несколько иначе.
Вернемся
к двойным интегралам: пусть теперь
функция
на множестве (в области)
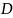 задает распределение плотности (например,
задает распределение плотности (например,
 означает, что в точке с координатами
означает, что в точке с координатами
 плотность равна
плотность равна
 ).
Тогда двойной интеграл от
вернет массу области
.
Это называется физическим
смыслом двойного интеграла:
).
Тогда двойной интеграл от
вернет массу области
.
Это называется физическим
смыслом двойного интеграла:
 – масса пластины
с распределением плотности
– масса пластины
с распределением плотности

И
вот экстраполяция физического смысла
двойного интеграла на тройной интеграл
уже понятна: тройной интеграл по
поверхности
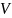 от функции
от функции
 равен массе тела
равен массе тела
( – функция распределения плотности,
только теперь не на плоскости
– функция распределения плотности,
только теперь не на плоскости
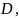 а внутри поверхности
).
а внутри поверхности
).
 –
масса тела
с распределением плотности
–
масса тела
с распределением плотности

Замечание:
здесь и далее: поверхность записывается
как
 однако общепринятого обозначения нет,
что может вызвать некоторые трудности.
–
не объем! Буква выбрана так лишь чтобы
подчеркнуть, что интегрирование
происходит по трехмерной замкнутой
поверхности.
однако общепринятого обозначения нет,
что может вызвать некоторые трудности.
–
не объем! Буква выбрана так лишь чтобы
подчеркнуть, что интегрирование
происходит по трехмерной замкнутой
поверхности.
Свойства двойных интегралов полностью переносятся и на тройные, поэтому расписывать их нет смысла.
Перейдем к расчетам.
Чтобы взять двойной интеграл, мы сводили его к повторному. Для того, чтобы взять тройной интеграл – сначала надо его свести к двойному, а затем двойной свести к повторному.
Пусть имеется поверхность и функция распределения плотности внутри этой поверхности
О братите
внимание: оси не подписаны, поскольку
их можно поменять местами заменой
переменных. Без ограничений общности
будем считать, что вверх направлена ось
братите
внимание: оси не подписаны, поскольку
их можно поменять местами заменой
переменных. Без ограничений общности
будем считать, что вверх направлена ось
 ,
а «тень» поверхность отбрасывает на
плоскость
,
а «тень» поверхность отбрасывает на
плоскость
 .
.
План расстановки пределов тройных интегралов в декартовой системе координат тривиален:
Выбрать ось «направления» - то есть ось высоты. Повторюсь: эта ось может быть любой, и
 и
и
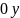 и
и
 .
Выбирается исходя из ситуации. (см
пример
2).
.
Выбирается исходя из ситуации. (см
пример
2).Найти пределы по данной оси. Поступаем по аналогии с двойными интегралами: нужно провести прямую, параллельную выбранной оси (в нашем случае ), из минус бесконечности, и найти количество точек пересечения с поверхностью (Поверхность называется правильной в выбранном направлении, если пересечений не больше двух). Далее всевозможные точки первого пересечения будут некоторой поверхностью
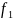 (
(
 в нашем случае), а вторые -
в нашем случае), а вторые -
 (
(
 в нашем случае)
Грубо
говоря, поверхность разбивается на две
половины – нижнюю и верхнюю. Можно
придумать ассоциацию: если поверхность
– это орех, то нижняя граница интегрирования
по ореху – нижняя половина скорлупы,
а верхняя граница – верхняя.
в нашем случае)
Грубо
говоря, поверхность разбивается на две
половины – нижнюю и верхнюю. Можно
придумать ассоциацию: если поверхность
– это орех, то нижняя граница интегрирования
по ореху – нижняя половина скорлупы,
а верхняя граница – верхняя.
Найти проекцию поверхности на плоскость, перпендикулярную оси, выбранной в пункте 1 Например если в пункте 1 была выбрана ось , то надо найти проекцию на плоскость
 .
.Перейти к двойному интегралу:
 где
где
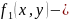 уравнение
«входа»,
уравнение
«входа»,
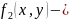 уравнение
«выхода»
уравнение
«выхода»
Замечания:
Аналогично замечанию (a) из предыдущего конспекта: в выражении (7) между
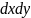 и
и
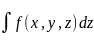 не
стоит знак умножения:
не
стоит знак умножения:

А
 налогично
замечанию (b):
Результатом
тройного интеграла является масса,
то есть число.
Значит пределы интегрирования внутреннего
интеграла – функции от тех же переменных,
по которым берется внешний двойной
интеграл
налогично
замечанию (b):
Результатом
тройного интеграла является масса,
то есть число.
Значит пределы интегрирования внутреннего
интеграла – функции от тех же переменных,
по которым берется внешний двойной
интеграл
Не стоит забывать, что в трехмерном пространстве есть выбор из трех осей, соответственно, за направляющую ось можно выбрать как , так и или . Для удобства пара рекомендаций: 1. Выбирайте ось, в направлении которой поверхность правильная 2. Если поверхность правильна в нескольких направлениях – выбирайте то, при котором проекция на перпендикулярную ему плоскость представляет собой простейшую область .
Пример 1:
(Сложность
-
 АВ)
АВ)
Расставить
пределы интегрирования в декартовой
системе координат для нахождения массы
тела
,
заданного функцией
 с
распределением плотности
с
распределением плотности
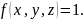
Решение:
 поверхность второго
рода. Для таких поверхностей есть золотое
правило – если сразу непонятно, какая
именно перед нами поверхность – смотрим
сечения плоскостями, параллельными
поверхность второго
рода. Для таких поверхностей есть золотое
правило – если сразу непонятно, какая
именно перед нами поверхность – смотрим
сечения плоскостями, параллельными
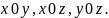
Сечение плоскостью

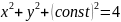 – это уравнения окружностей
– это уравнения окружностейСечение плоскостью

 – уравнения окружностей
– уравнения окружностейСечение плоскостью
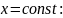
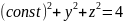 – тоже уравнения окружностей
– тоже уравнения окружностей
- во всех сечениях
окружности -
сфера
с радиусом
 и центром в
и центром в

Изобразим ее:
О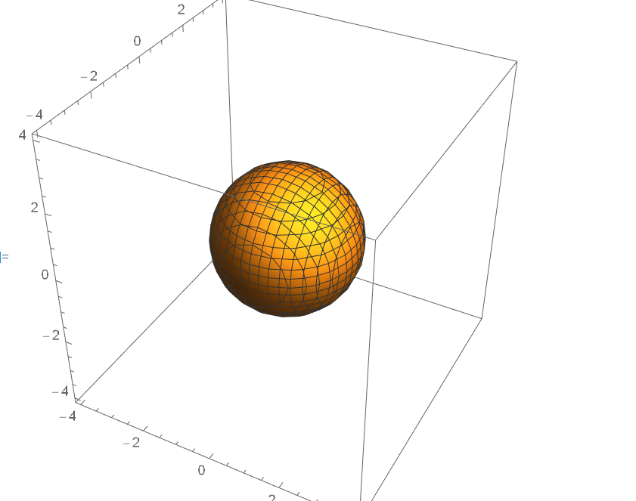 чевидно,
что сфера правильна во всех трех
направлениях. Выберем, например,
направление
.
Тогда внутренний интеграл по
чевидно,
что сфера правильна во всех трех
направлениях. Выберем, например,
направление
.
Тогда внутренний интеграл по
 а
меняется от нижней половины сферы до
верхней:
а
меняется от нижней половины сферы до
верхней:
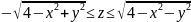
Проекция
на
плоскость, перпендикулярную
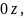 представляет из себя
представляет из себя
 - окружность радиуса 2
- окружность радиуса 2
Получаем
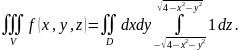
Теперь надо расставить
пределы интегрирования по
(по
проекции на ось, перпендикулярной
выбранному направлению), а это мы уже
делать умеем. Например, будем интегрировать
сначала по
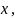 затем
по
затем
по
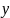 .
Значит
.
Значит

Если вы не понимаете, почему это так – обратитесь к первой части конспекта, сейчас я полагаюсь на то, что материал по двойным интегралам усвоен.
Запишем окончательно:
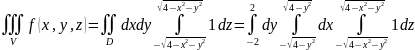
Предлагаю обратить
особое внимание на замечания (b)
из обоих конспектов: это может спасти
вас от ошибок. Например, произведем
проверку в нашем решении: пределы
внутреннего интеграла зависят от
 и
дальнейшее интегрирование производится
по
и
дальнейшее интегрирование производится
по
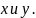 Пределы внутреннего повторного интеграла
зависят только от
Пределы внутреннего повторного интеграла
зависят только от
 и
внешний интеграл берется по
.
Пределы же внешнего интеграла – числа.
Задание алгебраически решено верно.
и
внешний интеграл берется по
.
Пределы же внешнего интеграла – числа.
Задание алгебраически решено верно.
Пример 2:
(Сложность –
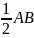 )
)
Расставить пределы
интегрирования и найти массу тела
 С распределением плотности
С распределением плотности
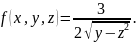
Для начала найдем сечения поверхности второго порядка (необходимо по очереди построить все уравнения, которыми задано затем найти замкнутую область).
Сечение плоскостью
 – внутренние области парабол
– внутренние области парабол
Сечение плоскостью
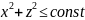 – внутренняя область окружностей
радиуса
– внутренняя область окружностей
радиуса

Сечение плоскостью
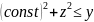 – внутренняя область парабол.
– внутренняя область парабол.
В сечениях имеются две параболы и окружности. Перед нами эллиптический параболоид1.
 положительные
полупространства,
отсекаемые плоскостями
положительные
полупространства,
отсекаемые плоскостями
 Изобразим
Изобразим


Из построения (рис 1) видно, что поверхность - светло – зеленая часть эллиптического параболоида. (рис 2)
Теперь надо выбрать направляющую ось.
Понятно, правильна во всех трех направлениях (прямые, параллельные любой из осей пересекают не более, чем в двух точках. Замечание: бесконечное количество точек в пересечении отсекаем открытым промежутком)
Все
проекции эллиптического цилиндра на
координатные плоскости мы уже рассмотрели
– это параболы и окружности. Однако,
плоскости
 «отрежут» часть проекции:
«отрежут» часть проекции: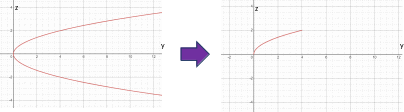

Здесь
не все так просто. В этом и прелесть
данных задач – нужно найти оптимальный
вариант. Посмотрите внимательно: если
мы выберем за направляющую ось
,
расставить пределы по
 будет проблематично. Действительно,
будет меняться от левой (на рис 2) части
до правой:
будет проблематично. Действительно,
будет меняться от левой (на рис 2) части
до правой:
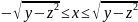 ,
и интеграл будет иметь вид
,
и интеграл будет иметь вид
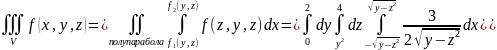
Если
же выбрать за направляющую ось
,
то
 ,
но расставлять пределы по окружности
неприятно:
,
но расставлять пределы по окружности
неприятно:
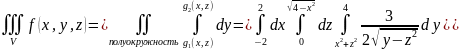
А теперь я смело заявляю: первый интеграл вы возьмёте за минуту, а второй не возьмёте.
Очень важно обращать внимание на интегрируемую функцию: в данном случае она подозрительно похожа на пределы интегрирования во внутреннем интеграле первого выражения…


Пример 3 (для самостоятельного решения)
(Сложность
–
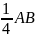 )
)
замкнутая поверхность,
ограниченная следующими уравнениями:

Распределение
плотности

Р асставить
пределы интегрирования оптимальным
способом и найти массу
.
асставить
пределы интегрирования оптимальным
способом и найти массу
.
Замена переменных в тройном интеграле. Сферическая и цилиндрическая замены.
Предупреждение: если вы еще не прочитали и не усвоили замену в двойном интеграле – самое время прочитать конспект №1. Здесь будет много ссылок на уже объясненный материал.
Пусть
функция распределения плотности
 интегрируема внутри поверхности
.
интегрируема внутри поверхности
.
Произведем замену переменных:
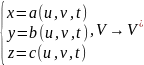
( функции от трех переменных).
функции от трех переменных).
Так же, как и в двойных интегралах, придется считать якобиан, который так же не должен быть вырожденным:
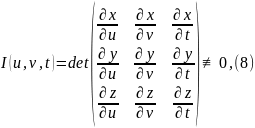
Свойство
обратимости:

Формула замены переменных2:

Системы координат
Декартова система координат в трехмерном пространстве всем хорошо известна – точка задается радиус-вектором, имеющим три координаты – длины проекций на оси
 .
.Ц
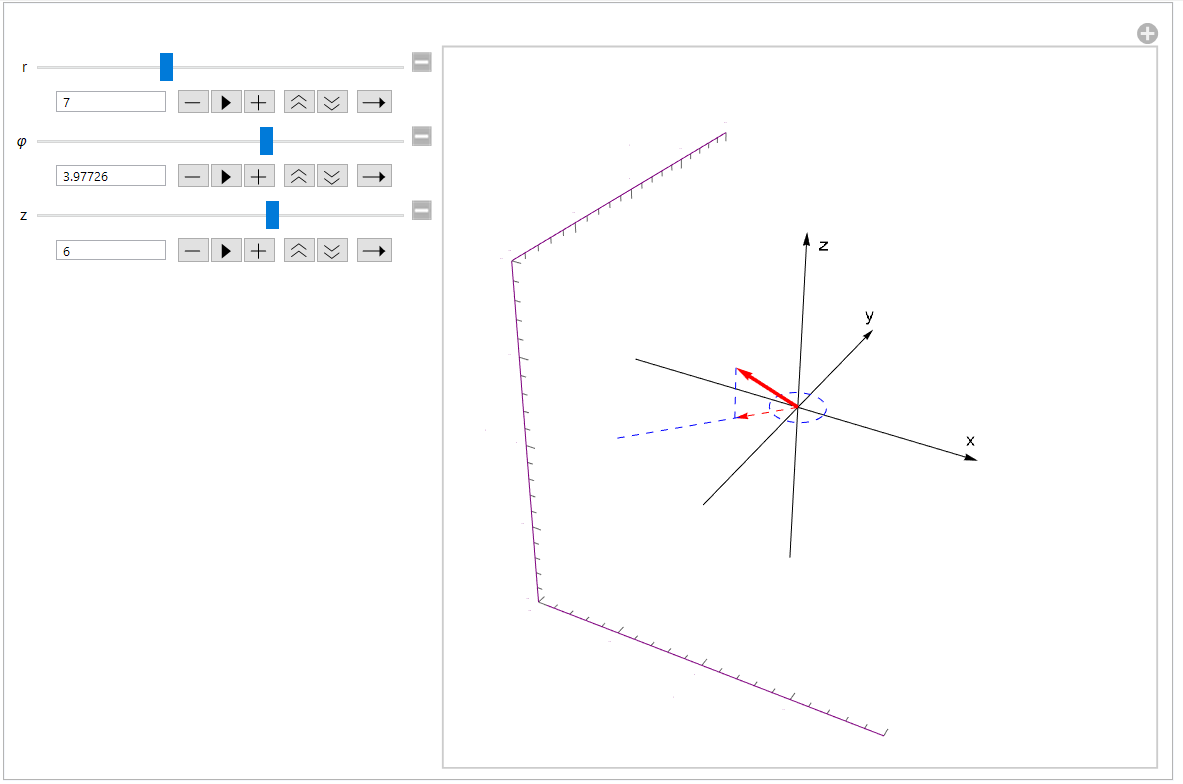 илиндрическая
система координат.
По
сути – это полярная система координат,
с добавлением третьей координаты –
«высоты» над плоскостью полярных
координат.
Таким образом точка
пространства задаётся при помощи
1.
Расстояния
илиндрическая
система координат.
По
сути – это полярная система координат,
с добавлением третьей координаты –
«высоты» над плоскостью полярных
координат.
Таким образом точка
пространства задаётся при помощи
1.
Расстояния
 от центра координат до проекции точки
на плоскость
2.
Углом
от центра координат до проекции точки
на плоскость
2.
Углом
 между осью
и проекцией радиус–вектора на плоскость
3.
Высоты
точки
над плоскостью
между осью
и проекцией радиус–вектора на плоскость
3.
Высоты
точки
над плоскостью
 Обратите
внимание: точно так же, как и в полярной
системе
Обратите
внимание: точно так же, как и в полярной
системе

С
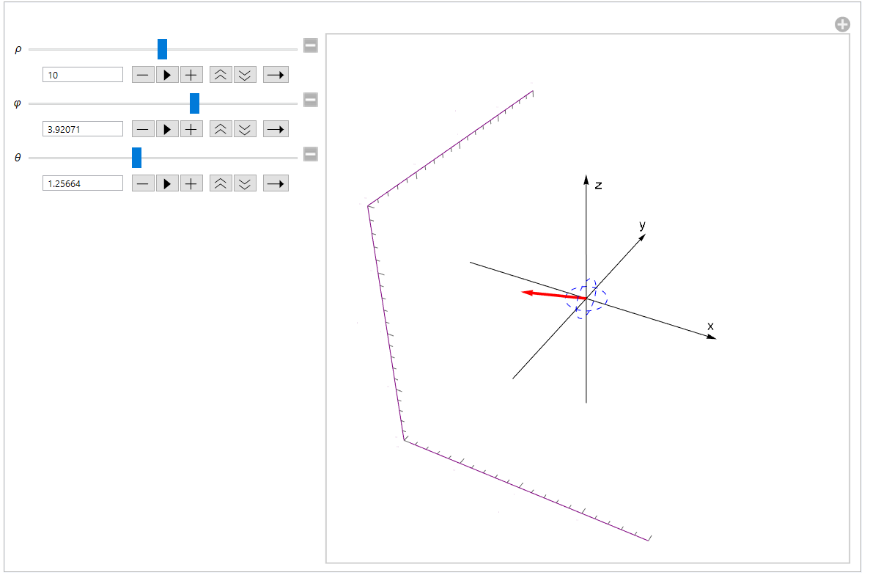 ферическая
система координат
Точка
в пространстве определяется с помощью
1. Расстояния
до
нее от центра координат
2. Угла
между
осью
и проекцией радиус-вектора точки на
плоскость
ферическая
система координат
Точка
в пространстве определяется с помощью
1. Расстояния
до
нее от центра координат
2. Угла
между
осью
и проекцией радиус-вектора точки на
плоскость
 3. Угла
3. Угла
 между
остью
и
радиус-вектором.
между
остью
и
радиус-вектором.
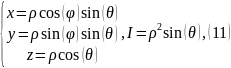 Важное
замечание:
Очевидно,
что
Важное
замечание:
Очевидно,
что
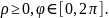 Но есть еще одно ограничение:
Но есть еще одно ограничение:
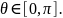 Объясняется
этот факт достаточно несложно, (но в
первый раз может взорвать мозг): точка,
с координатой
Объясняется
этот факт достаточно несложно, (но в
первый раз может взорвать мозг): точка,
с координатой
 ),
если
),
если
 ,
это то же самое, что и точка
,
это то же самое, что и точка
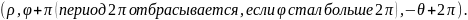 Поэтому,
чтобы избежать неоднозначности, вводится
ограничение
Поэтому,
чтобы избежать неоднозначности, вводится
ограничение
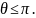
Я понимаю, что понять материал по сухому тесту и паре картинок невозможно. Поэтому предлагаю опробовать системы координат туть. Особо важным является замечание в предыдущем пункте, его необходимо осознать. Если непонятно – бейте тревогу.
Еще один крайне важный момент: следует понимать, что, например, замена вида
 – тоже будет
цилиндрической заменой.
Совершенно все равно, какую плоскость
мы выберем в качестве полярной. Но как
только мы выбрали плоскость – ось,
перпендикулярная ей, становится остью
«высоты».
В сферической системе
координат то же самое – никакой
привязки к декартовым осям на
самом деле нет!
Замена
– тоже будет
цилиндрической заменой.
Совершенно все равно, какую плоскость
мы выберем в качестве полярной. Но как
только мы выбрали плоскость – ось,
перпендикулярная ей, становится остью
«высоты».
В сферической системе
координат то же самое – никакой
привязки к декартовым осям на
самом деле нет!
Замена
 -
тоже сферическая.
-
тоже сферическая.
Расставлять пределы в цилиндрической системе координат не сложнее, чем в декартовой: сначала необходимо произвести цилиндрическую замену (пользуясь (10)), затем перейти к двойному интегралу точно так же, как и в декартовой системе координат. Отличие в том, что расставлять пределы в двойном интеграле нужно будет уже в полярной системе координат.
В
сферической же системе необходимо найти
всевозможные точки «входа» и «выхода»
радиус векторов
(обратите
внимание, не прямых, параллельных
направляющей оси, а радиус-векторов),
затем «зажать» поверхность между
крайними углами
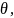 после найти предельные углы
после найти предельные углы
 Подробнее
это будет рассмотрено в следующем
примере.
Подробнее
это будет рассмотрено в следующем
примере.
Итак,
Пример 3: (нет, я не украл у АВ, я реквизировал)

Расставить пределы интегрирования тремя способами (в трех системах координат)
Решение:
По уже отработанной схеме, сначала рассматриваем сечения
Сечение плоскостью
 –
внутренняя области гипербол с асимптотами
–
внутренняя области гипербол с асимптотами
 .
.
*напоминаю, как находятся сечения: фиксируем переменную, заменяем ее на и строим кривые. const – это зафиксированная переменная.
Сечение плоскостью
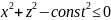 – внутренняя область окружностей
радиуса
– внутренняя область окружностей
радиуса

Сечение плоскостью
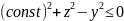 – внутренняя область гипербол с
асимптотами
– внутренняя область гипербол с
асимптотами
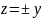 .
.
Уравнение
 соответствует внутренней части конуса.
Однако, каноническое уравнение конуса
соответствует внутренней части конуса.
Однако, каноническое уравнение конуса
 (у
нас он повернут). В таких случаях, чтобы
не путаться, я рекомендую сделать замену
переменных таким образом, чтобы свести
поверхность к каноническому виду. Таким
образом оси
(у
нас он повернут). В таких случаях, чтобы
не путаться, я рекомендую сделать замену
переменных таким образом, чтобы свести
поверхность к каноническому виду. Таким
образом оси
 надо поменять местами.
надо поменять местами.
Очевидно,
что якобиан такой замены тождественно
равен единице (поворот ничего не меняет).
Поэтому можно записать новую поверхность
 .
.
Я
намеренно переставил местами
 и
в уравнении распределения плотности,
чтобы подчеркнуть, что замена производится
и в ней. И
еще напоминаю,
что поменять местами переменные надо
будет и в сечениях.
и
в уравнении распределения плотности,
чтобы подчеркнуть, что замена производится
и в ней. И
еще напоминаю,
что поменять местами переменные надо
будет и в сечениях.
Полагаю,
что уравнение
 всем известно – это сфера радиуса 2. В
данном случае ее поверхность будет
«шапкой» конуса. Теперь изобразим
поверхность. Сначала все проекции,
затем аккуратно объединяем3:
всем известно – это сфера радиуса 2. В
данном случае ее поверхность будет
«шапкой» конуса. Теперь изобразим
поверхность. Сначала все проекции,
затем аккуратно объединяем3:
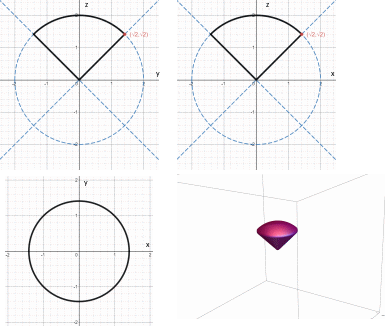
Полагаю,
требуется некоторое пояснение к
проекциям. Проекцией
на
будет окружность, по которой пересекаются
сфера и конус. Ее уравнение можно найти
аналитически:

Это означает, что
пересечение происходит на «высоте»
.
Уравнение пересечения
 или
или
 .
.
Проекции
на плоскости
 одинаковы, и получаются путем подстановки
в полученных на первом этапе решения
сечениях 0 вместо
одинаковы, и получаются путем подстановки
в полученных на первом этапе решения
сечениях 0 вместо

Здесь можно пощупать поверхность. Теперь расставим пределы интегрирования.
Декартова система координат.
З аметим,
что поверхность симметрична относительно
плоскости
аметим,
что поверхность симметрична относительно
плоскости
 ,
а функция плотности четна относительно
всех осей и координатных плоскостей.
Значит достаточно посчитать массу
только левой половины:
Здесь
будет меняться от левой половины конуса
до шапки:
,
а функция плотности четна относительно
всех осей и координатных плоскостей.
Значит достаточно посчитать массу
только левой половины:
Здесь
будет меняться от левой половины конуса
до шапки:
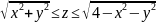 .
.
Т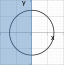 еперь
надо расставить пределы двойного
интеграла:
еперь
надо расставить пределы двойного
интеграла:
поскольку
проекция половины поверхности на
плоскость
есть полуокружность
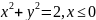 (уравнение окружности было найдено
здесь)
то
(уравнение окружности было найдено
здесь)
то
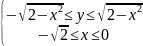
В результате
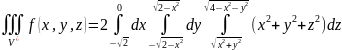
Цилиндрическая система координат
Все отличие от декартовой в том, что пределы двойного интеграла расставляются полярной системе координат.
Все уравнения должны быть переведены в цилиндрические координаты:
 – уравнение сферы
– уравнение сферы
 – уравнение конуса
– уравнение конуса
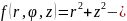 уравнение распределения
плотности
уравнение распределения
плотности
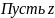 все так же меняется
от левой половины конуса до сферы:
все так же меняется
от левой половины конуса до сферы:
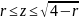 .
.
Пределы двойного интеграла по проекции на :
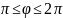 (левая половина
полуокружности, см изображение выше),
(левая половина
полуокружности, см изображение выше),
 .
.
Теперь
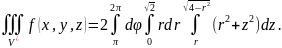
Сферическая система координат.
И
вот выясняется, что это тот пример, где
сферическая система координат на коне
(не придумал шутку про сферического
коня в вакууме, pardon).
меняется от нуля до радиуса сферы:
 Углы
Углы
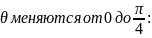
 Углы
определяются по проекции на плоскость,
перпендикулярную оси направления (нашем
случае по проекции
Углы
определяются по проекции на плоскость,
перпендикулярную оси направления (нашем
случае по проекции
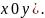 Но эта проекция – окружность. Значит
принимает
все возможные значения:
Но эта проекция – окружность. Значит
принимает
все возможные значения:
 .
.
Осталось
перевести
 в сферические координаты:
в сферические координаты:

Тогда интеграл будет иметь вид

Попробуйте расставить пределы интегрирования в примере 2, используя сферическую и цилиндрическую системы координат, для закрепления материала.
1
Если такие рассуждения Вам непонятны
– вот еще подсказка:

2
Для тренировки рекомендую доказать,
что якобиан цилиндрической замены
равен
,
а сферической
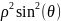
3 Когда это будет происходить автоматически – так подробно расписывать будет не нужно. В решении просто указаны все шаги, чтобы читатель смог полностью уловить суть.
