2.3.Дискретный режим работы НР, СМ без запаса комплекта деталей
Рис. 2.7. Граф третьей модели
При этом
|
|
|
λ |
k |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pk = Cnk |
µ |
|
P0 = CnkαkP0, k = 0, m |
|
|
|
||||||
|
|
( ) |
n! |
m+r |
|
|
(5) |
||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pm+r = |
|
|
|
|
α |
P0, r = 1 , n |
|
m, |
||||
|
|
|
|
|
− |
||||||||
|
|
mrm!(m − n − r)! |
|
|
|
|
|
|
|||||
аP0 находится из условия (3). Граф модели изображен на Рис. 2.8.
Уравненения Колмагорова модели:
dp0 |
= −3λp0 + µp1 |
|
dt |
||
dp1 |
= −(2λ + µ)p1 + 3λp0 + 2µp2 |
|
|
||
dt |
||
dp2 |
(6) |
|
= −(λ + 2µ)p2 + 2λp1 + 2µp3 |
||
dt |
||
dp3 |
= −2µp3 + λp2. |
|
|
||
dt |
Рис. 2.8. Расчетный граф третьей модели
Таблицы установившихся значений ненормированных и нормированных вероятно-
стей приведены в Табл. 2.5 и Табл. 2.6 соответственно, графики переходных процессов на Рис. 2.9.
10
Таблица 2.5: Распределение вероятностей, третья модель, без нормировки
|
k |
|
0 |
|
|
1 |
|
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pk |
|
1 |
45 |
≈ 6.43 |
675 |
≈ 13.78 |
10121 |
≈ 14.76 |
||||
|
|
|
|
|
|
|
|
|
|
||||
|
P0 |
|
7 |
49 |
686 |
||||||||
Таблица 2.6: Распределение вероятностей (третья модель, с точностью 10−2)
k |
|
0 |
1 |
2 |
3 |
|
|
|
|
|
|
Pk |
|
0.03 |
0.18 |
0.38 |
0.41 |
Рис. 2.9. Переходные процессы третьей модели
Характеристики замкнутой СМО:
1. Среднее число технических устройств, находящихся в очереди на обслуживание
n∑−m
r¯ = rPm+r ≈ 0.41.
r=1
2. Среднее число обслуживаемых технических устройств
∑k |
∑ |
m |
n−m |
¯ |
Pm+r ≈ 1.76. |
k = kPk + m |
|
=0 |
r=1 |
11
3. Среднее число неработающих технических устройств
¯ ¯
l = r¯ + k ≈ 2.17.
4. Вероятность того, что техническое устройство будет простаивать
β= nl ≈ 0.72.
5.Вероятность того, что техническое устройство будет работать
γ= 1 − β ≈ 0.28.
6.Среднее число каналов, занятых обслуживанием¯
∑k |
∑ |
m−1 |
n |
z¯ = |
kPk + m Pk ≈ 1.76. |
=0 |
k=m |
7.Среднее число технических устройств, обслуживаемых в единицу времени (произ-
водительность системы массового обслуживания или абсолютная пропускная спо-
собность СМО)
λ0 = zµ¯ ≈ 0.35.
12
2.4.Дискретный режим работы НР, СМ с запасом комплекта деталей
Модель системы приведена на Рис. 2.10.
Рис. 2.10. Граф четвертой модели
Для нее
dp02 = −3λp02 + 2µp01 dt
dp02 = −(3λ + 2µ)p01 + 3λp02 + µp0 dt
dp0 |
= −(3λ + µ)p0 + 3λp01 + µp1 |
|
dt |
||
dp1 |
(7) |
|
= −(2λ + µ)p1 + 3λp0 + 2µp2 |
||
dt |
||
dp2 |
= −(λ + 2µ)p2 + 2λp1 + 2µp3 |
|
|
||
dt |
dpdt3 = −2µp3 + λp2.
На основании численного решения (Рис. 2.11, Рис. 2.12) составлена таблица веро-
ятсностей Табл. 2.7.
Рис. 2.11. Расчетный граф четвертой модели
13
Рис. 2.12. Переходные процессы четвертой модели
Таблица 2.7: Распределение вероятностей (четвертая модель)
k |
|
0 |
1 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
|
Pk, % |
|
0.1 |
0.4 |
2.8 |
17.8 |
38.1 |
40.8 |
|
|
|
|
|
|
|
|
14
3.Оптимизация выбранного режима работы сбороч-
ного цеха
Для дальнейшего анализа выбрана модель №2. Для нее при заданных параметрах достигаются наилучшие значения метрик: вероятность отказа меньше 1%, среднее число занятых каналов близко к максимально возможному. По сравнению с первой моделью достигаются лучшие пропускные способности, а по сравнению с третьей — меньшая вероятность простоя.
Экспериментальные данные и рассчитанные по ним значения характеристик СМО приведены в Табл. 3.1.
Таблица 3.1: Характеристики СМО как функции от варьируемого параметра
λ |
|
1 |
0.25 |
0.2 |
0.1 |
0.05 |
0.01 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P0, % |
|
0.76 |
21.69 |
40.32 |
60.61 |
78.13 |
95.24 |
|
|
|
|
|
|
|
|
P1, % |
|
3.79 |
32.54 |
36.29 |
30.30 |
19.53 |
4.76 |
|
|
|
|
|
|
|
|
P2, % |
|
9.48 |
24.51 |
16.53 |
7.88 |
2.34 |
0.00 |
|
|
|
|
|
|
|
|
P3, % |
|
15.79 |
12.15 |
4.84 |
1.21 |
0.00 |
0.00 |
|
|
|
|
|
|
|
|
P31, % |
|
26.32 |
6.07 |
1.61 |
0.00 |
0.00 |
0.00 |
|
|
|
|
|
|
|
|
P32, % |
|
43.86 |
3.04 |
0.40 |
0.00 |
0.00 |
0.00 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
pотк, % |
|
43.87 |
1.23 |
0.75 |
0.04 |
0.00 |
0.00 |
q, % |
|
56.13 |
98.77 |
99.25 |
99.96 |
100.00 |
100.00 |
|
|
|
|
|
|
|
|
A, % |
|
56.13 |
24.69 |
19.85 |
10.00 |
5.00 |
1.00 |
|
|
|
|
|
|
|
|
¯ |
|
2.81 |
1.45 |
0.90 |
0.50 |
0.24 |
0.05 |
k |
|
||||||
r¯ |
|
114.05 |
12.15 |
2.42 |
0.00 |
0.00 |
0.00 |
|
|
|
|
|
|
|
|
¯ |
|
3.95 |
5.42 |
5.08 |
5.00 |
5.00 |
5.00 |
tc |
|
||||||
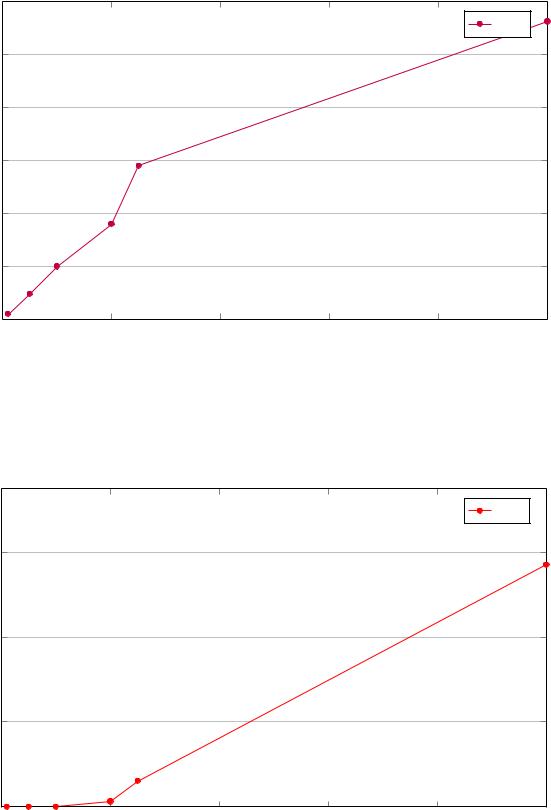
Графики зависимостей характеристик приведены на рисунках ниже.
Исходя из наблюдений можно сделать вывод, что для оптимизации работы следует увеличить время обработки одной заявки или интенсивность потока заявок (уменьшить
λ). Это позволит повысить число занятых каналов и максимизировать все метрики.
15
|
100 |
|
|
|
|
Pотк(λ) |
|
|
|
|
|
q(λ) |
|
|
|
|
|
|
|
|
|
80 |
|
|
|
|
|
/ q, % |
60 |
|
|
|
|
|
, % |
|
|
|
|
|
|
отк |
40 |
|
|
|
|
|
P |
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
|
|
|
λ |
|
|
|
|
|
|
Рис. 3.1 |
|
|
|
|
70 |
|
|
|
|
|
|
|
|
|
|
|
A(λ) |
60
50
40 %, A 30
20
10
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
λ
Рис. 3.2
16
|
3 |
|
|
|
|
|
|
|
|
|
|
|
¯ |
|
|
|
|
|
|
k(λ) |
|
2.5 |
|
|
|
|
|
|
2 |
|
|
|
|
|
k¯ |
1.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
|
|
|
λ |
|
|
|
|
|
|
Рис. 3.3 |
|
|
|
|
|
|
|
|
|
r¯(λ) |
|
120 |
|
|
|
|
|
r¯ |
80 |
|
|
|
|
|
|
|
|
|
|
|
|
|
40 |
|
|
|
|
|
|
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
|
|
|
λ |
|
|
|
|
|
|
Рис. 3.4 |
|
|
|
|
|
|
17 |
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
t¯c(λ) |
|
5 |
|
|
|
|
|
|
4 |
|
|
|
|
|
c |
|
|
|
|
|
|
¯ |
3 |
|
|
|
|
|
t |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
0 |
0.2 |
0.4 |
0.6 |
0.8 |
1 |
|
|
|
λ |
|
|
|
|
|
|
Рис. 3.5 |
|
|
|
18