Лаб3 / МОТС_лабка3

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В. И. Ульянова (Ленина)

Кафедр АПУ

отчет

по лабораторной работе №3

по дисциплине «Математические основы теории систем»

Тема: Спектр. Ряд Фурье.

Студенты гр. 0392		Стаськова А. Р.
		Частухин Д. А.
		Иванов С. К.
Преподаватель		Гульванский В.В.

Санкт-Петербург

2022

Цель работы:

• Знакомство со спектральным представлением периодических и случайных процессов;

• Изучение взаимосвязи преобразований сигналов во временной и частотной областях;

• Оценка дефектов дискретного преобразования Фурье и методы их подавления.

Теоретические положения. Поставим задачу: представить некоторый сложный периодический процесс , заданный на интервале , в виде суммы простых периодических функций вида

.

Периодичность гарантирует, что в таком разложении будут присутствовать только гармоники кратных частот , – целое, . При 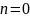получим постоянную составляющую, обычно записываемую в форме , а все разложение будет иметь вид:

Данное разложение называется рядом Фурье.

Коэффициенты этого ряда рассчитываются по формулам:

Если воспользоваться формулой Эйлера , получим более простую запись ряда Фурье в комплексной форме:

– коэффициенты ряда Фурье или спектр.

Совокупность функций называется базисом Фурье.

Комплексные коэффициенты обычно представляют в форме

– амплитудный спектр; – фазовый спектр; – реальная составляющая спектра; – мнимая составляющая спектра.

Для анализа непериодических процессов служит преобразование Фурье:

Широкое распространение спектрального представления сигналов объясняется следующими причинами:

• Гармонические функции – единственные, не меняющие своей формы при прохождении через линейную систему: может измениться только их амплитуда и фаза, но не форма, а, значит, не частота;

• Простота синтеза гармонического колебания – для этого достаточно иметь колебательный контур или любую другую резонансную систему. Разложить в спектр Фурье оптический сигнал может любая двояковыпуклая линза, радиосигналы в эфире тоже представлены электромагнитными волнами – гармониками ряда Фурье;

• Графическое представление спектральных коэффициентов на частотной оси – спектра сигнала – позволяет получить наглядную картину распределения в сигнале низких и высоких частот;

• Частотные характеристики используются не только для анализа сигналов, но и для анализа свойств динамических систем.

Чтобы построить спектр с помощью ДПФ (БПФ), надо определить следующие параметры:

• количество спектральных составляющих ;

• шаг между соседними частотами – разрешение по частоте ;

• частоту дискретизации ;

• минимальную (нижнюю) частоту спектра ;

• верхнюю частоту ;

• временной интервал анализа .

На самом деле, эти параметры жестко связаны друг с другом, и для однозначного построения спектра достаточно задать всего две величины.

Как правило, анализ начинается с выбора временной базы анализа и частоты дискретизации . При этом оказываются определенными и количество отсчетов сигнала , и минимальная частота спектра: . А поскольку количество спектральных коэффициентов равно количеству отсчетов сигнала , оказываются определенными и верхняя частота преобразования , и шаг между соседними частотами ƒ= .

Спектр сигнала (сейчас мы рассматриваем только вещественные функции) будет состоять из двух зеркально отраженных картин. Для комплексного спектра этого не происходит, однако в спектре появляются отрицательные частоты.

Теорема Котельникова: Любой сигнал , спектр которого не содержит составляющих с частотами выше некоторого значения , может быть без потерь информации представлен своими дискретными отсчетами , взятыми с интервалом , удовлетворяющим следующему неравенству: .

Преобразование Фурье в дискретной форме (ДПФ) имеет и другие недостатки. Главный из них – растекание спектра. Растекание спектра (англ. spectrum leakage) – эффект, возникающий вследствие финитности анализируемого сигнала (фактически бесконечный сигнал взвешивается финитным прямоугольным окном). Для подавления этого эффекта используют взвешивание сигнала специальными оконными функциями (окна Чебышева, Ханна, Парзена и т.д.).

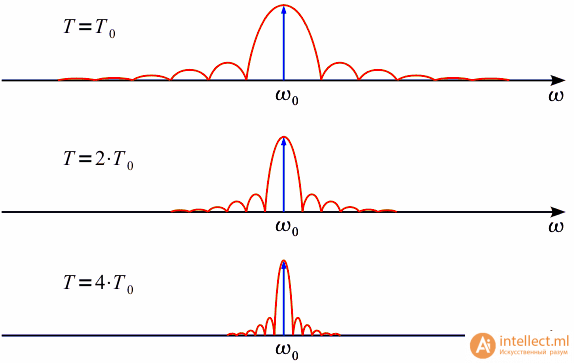
Рис. 1.1. Растекание спектра

При спектральном преобразовании сигнала могут использоваться и другие – не гармонические – функции. В этом случае говорят об обобщенном преобразовании Фурье: .

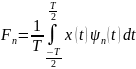Главные требования к функциям – их ортогональность и полнота.

Два вектора , называют взаимноортогональными, если их скалярное произведение равно нулю,

Если при этом норма каждого вектора равна 1, векторы называют ортонормальными.

Для любого вектора размерности (длины) можно найти и только ортогональных векторов. Такой набор векторов называют полной ортонормальной системой, или базисом -мерного линейного пространства.

Рассмотрим пример базиса (базис Уолша) в пространстве

Первый базис задается матрицей

или в графической форме (каждая функция – одна из строк матрицы )

Рис. 1.2. Базис Уолша

Исследуем его. Прежде всего, бросается в глаза равенство всех элементов матрицы . Это очень удобное свойство базисных функций: при умножении на такую функцию временные затраты минимальны. Первая строка базиса служит для выделения постоянной составляющей из исследуемого сигнала и в классических базисах все ее элементы равны единице. При этом все остальные функции не реагируют на постоянную составляющую вследствие симметричности их относительно нуля.

Приведем еще один весьма широко используемый базис – базис Хаара (Рис. 1.4):

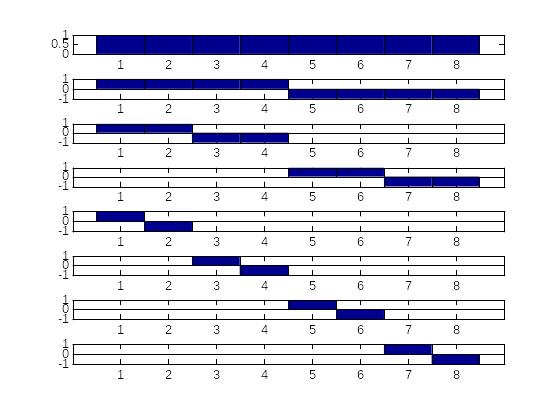
Рис. 1.3. Базис Хаара

Его главное достоинство – большое количество нулевых элементов. Это не только ускоряет вычисления спектра, но и обеспечивает сжатое представление сигналов с резкими перепадами. Это объясняется тем, что каждая функция (за исключением первых двух) выделяет только некоторую локальную область существования сигнала.

Для упрощения здесь базис Хаара приведен в ненормированной форме: чем уже импульс, тем меньше его энергия.

Выполнение работы.

1. Создали два сигнала Временной интервал – выбран так, чтобы более низкочастотный сигнал имел на нем 5 периодов, а частота дискретизации – чтобы на периоде сигнала высокой частоты укладывалось 10 отсчетов. Получен модуль спектра сигнала.

Рис. 2.1 Сигнал

Рис. 2.2 Сигнал

2. Построены спектры еще двух сигналов . Их вид определяется элементарными формулами тригонометрии.

Рис. 2.3 Сигнал

Рис. 2.4 Сигнал

3. Построили спектры функции Дирака. При смещении импульса меняется только фаза.

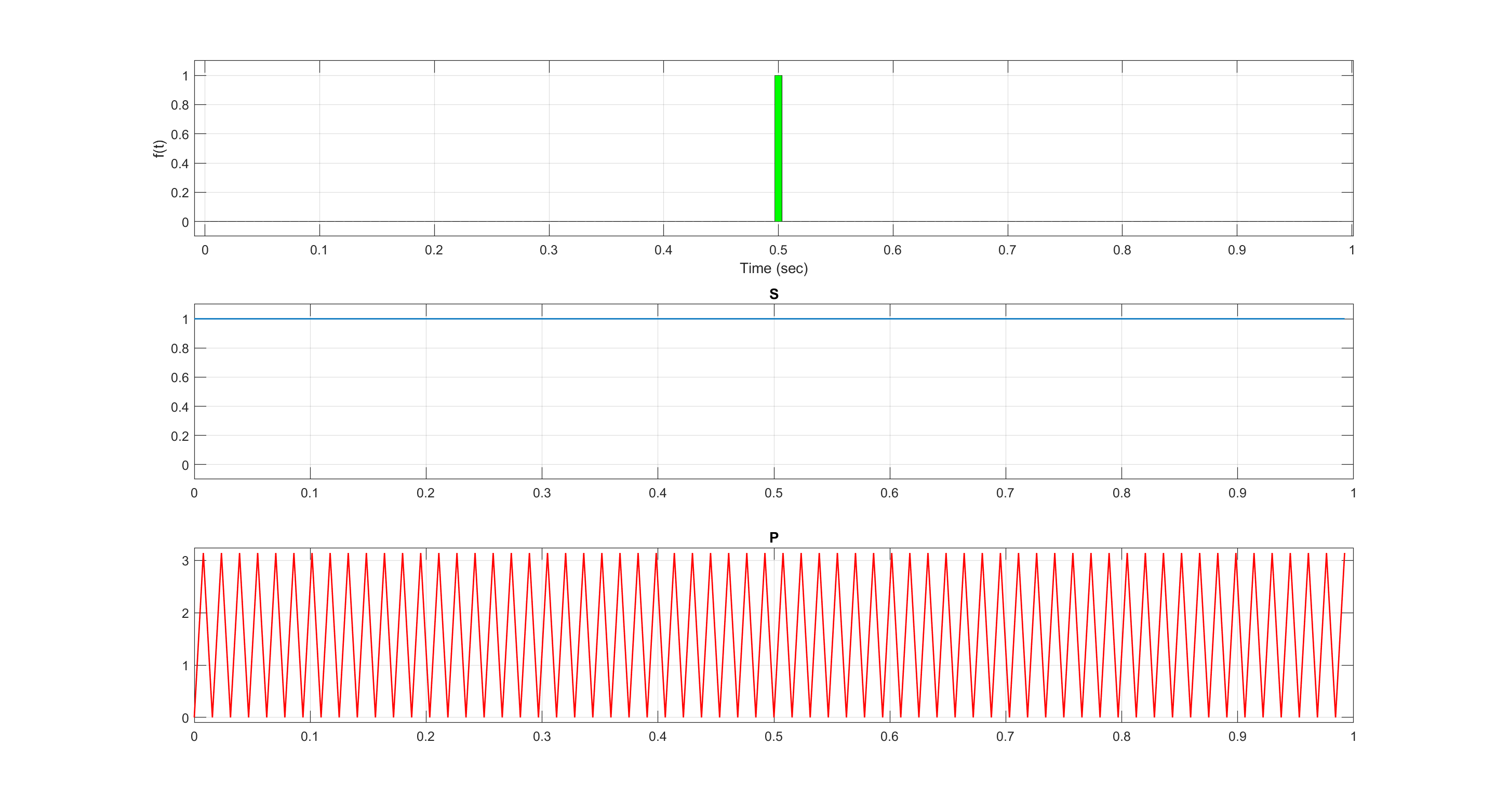
Рис. 2.5 импульс

4. В цикле последовательно увеличивая ширину нормированного (таким образом, чтобы площадь оставалась равна 1) импульса от отсчетов, пронаблюдали изменения его спектра.

Рис. 2.6 Спектры различных по длине импульсов.

5. На том же временном интервале построен спектр периодического прямоугольный сигнала со скважностью 2 (меандр) и количеством периодов, кратным двум.

Рис. 2.7 Периодический прямоугольный сигнал.

6. Построен спектр того же сигнала в базисе Уолша.

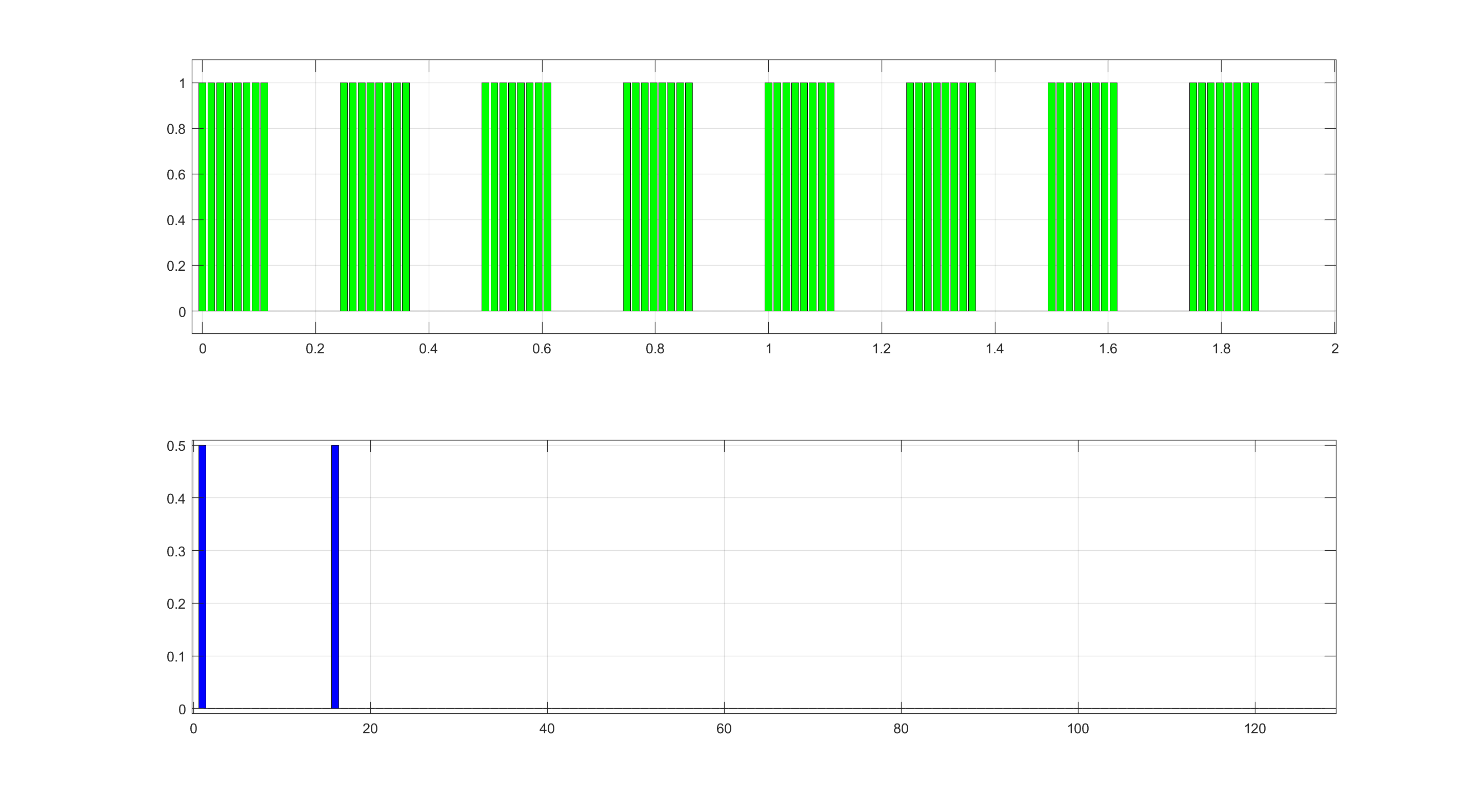
Рис. 2 8 Спектр импульса из 5) в базисе Уолша.

Вывод.

• Ознакомились со спектральным представлением периодических и случайных процессов;

• Изучили взаимосвязь преобразований сигналов во временной и частотной областях;

• Оценили дефекты дискретного преобразования Фурье.

Рис. 2.9 Кот.