
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедр АПУ
отчет
по лабораторной работе №1
по дисциплине «Математические основы теории систем»
Тема: Матричные преобразования и трехмерная графика.
Студенты гр. 0392 |
|
Стаськова А.Р. |
|
|
Частухин Д.А. |
|
|
Иванов С.К. |
Преподаватель |
|
Гульванский В.В. |
Санкт-Петербург
2022
Цель работы: освоение специфики матричных преобразований MATLAB и сравнительный анализ различных форм графического отображения результатов.
Теоретические
положения.
Пусть
дана функция двух аргументов
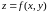 .
В области определения
.
В области определения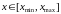 ,
,
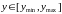 командой [X,Y]
= meshgrid(xgv,ygv)
создайте координатную сетку с заданным
шагом. Теперь можно создавать саму
функцию, например:
командой [X,Y]
= meshgrid(xgv,ygv)
создайте координатную сетку с заданным
шагом. Теперь можно создавать саму
функцию, например:
>>[x,y]=meshgrid(-10:0.3:10,-10:0.3:10);
>> z=(sin(x)./x).*(sin(y)./y);
>> surf(x,y,z)
Полученная поверхность приведена на рисунке 1.1. Можно произвольно выбрать шкалу цветовых оттенков (см. help colormap).
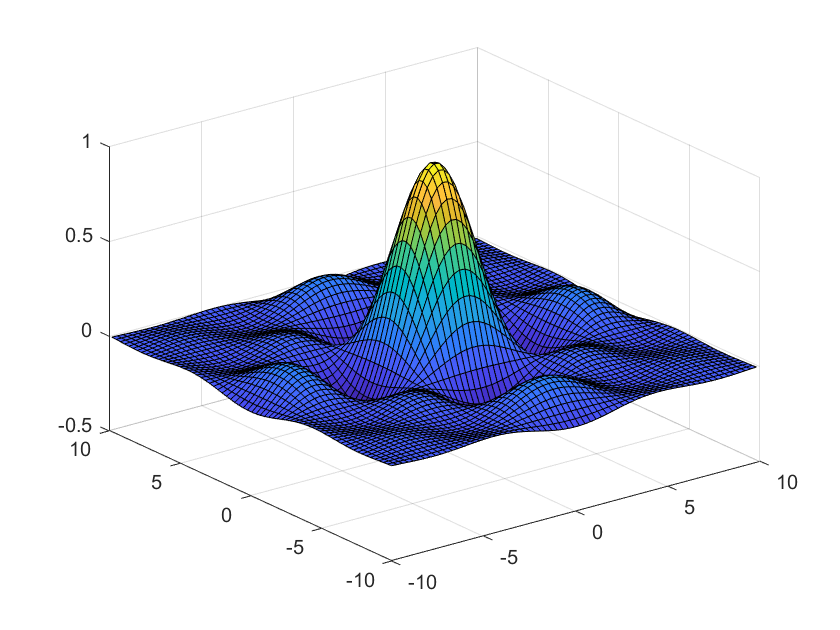
Рис. 1.1. Трехмерная поверхность
Второй способ состоит в формировании двух взаимно перпендикулярных плоскостей X и Y – аналогов двумерных осей ординат.
>> x=-10:10;
>> y=ones(1,21);
>> X=x'*y;
>> Y=y'*x;
Теперь используем координатные плоскости для построения конуса:
>> R1=sqrt(X.^2+Y.^2);
>> surf(X,Y,-R1);
или пирамиды (рис. 3.2):
>> R2=max(abs(X),abs(Y))
>> surf(X,Y,-R2);
Матричные операции, вычисление функций от матриц. Кратко напомним основные матричные операции.
Определитель
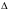 .
.
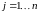 ,
,
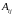 –
алгебраическое дополнение;
–
алгебраическое дополнение;
Обратная
матрица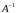 .
.
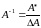
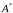 – союзная матрица;
– союзная матрица;
Умножение
матриц
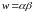 .
Элемент результирующей матрицы
.
Элемент результирующей матрицы
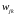 на
пересечении строки
на
пересечении строки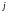 и столбца
и столбца
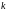 равен
сумме
попарных произведений элементов строки
матрицы
равен
сумме
попарных произведений элементов строки
матрицы
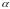 и столбца
матрицы
и столбца
матрицы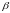 :
:
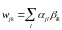
Возведение
в степень
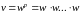 осуществляется
осуществляется
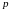 ‑кратным
умножением матрицы на себя.
‑кратным
умножением матрицы на себя.
Выполнение работы.
clear all
close all
x = -10:10;
y = ones(1, 21);
X = x'*y;
Y = y'*x;
Строим пирамиду, приавляя к матрице пирамиды единичную матрицу, чтобы определитель был отличен от нуля.
R = max(abs(X), abs(Y));
d = det(R);
R1 = R+eye(21);
d1
= det(R1);

Рис 2.1 Определитель.
Сравниваем результаты двух операций – обращения матрицы командой inv и поэлементного деления матрицы ones(n,n) на R.

Рис 2.2 Сравнение обращение и поэлементного деления.
R_inv = inv(R1);
R_ones = ones(21, 21)./R1;
figure('Name','?????????','NumberTitle','off');
%title('?????????');
subplot(1, 2, 1)
surf(X, Y, -R_inv)
title('inv');
subplot(1, 2, 2);
surf(X, Y, -R_ones)
title('./')
Сравниваем матричные операции sqrtm(A), logm(A), expm(A) с аналогичными операциями, выполняемыми поэлементно.
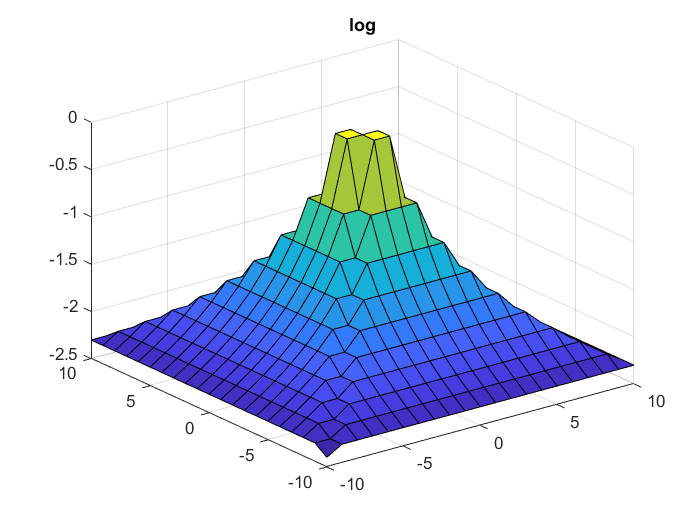
Рис 2 3 Матричный логарифм.
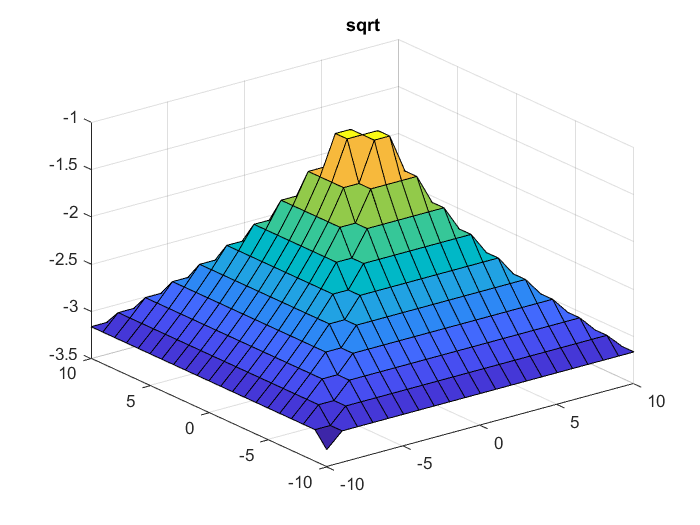
Рис 2.4 Матричное извлечение корня.
Поэлементные
операции логарифма и извлечение корня
невозможны, поскольку в матрице есть
отрицательные элементы.
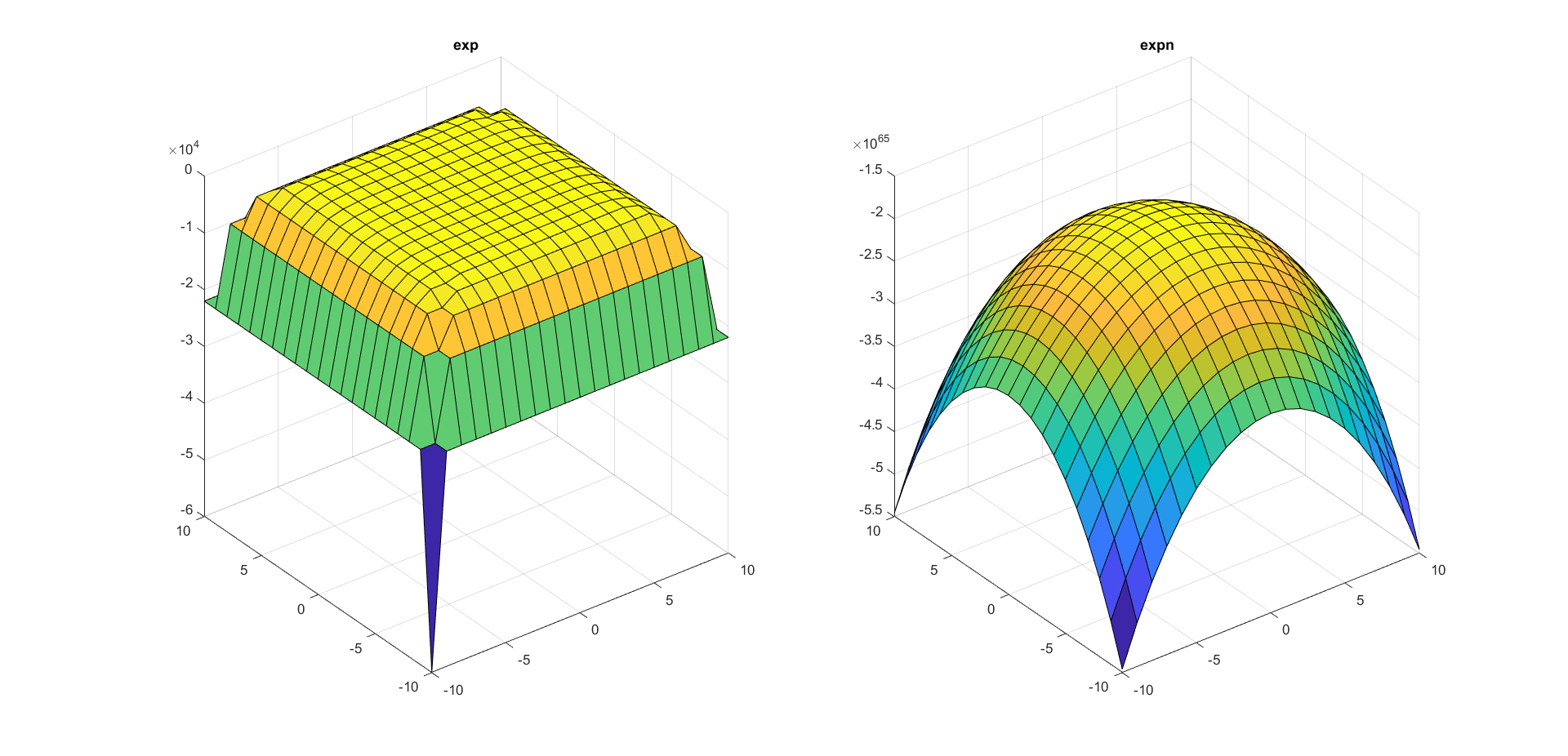
Рис 2.5 Сравнение матричного экспоненциала и поэлементной экпоненты
R_sqrtm = sqrtm(R1);
R_sqrt = sqrt(R1);
figure('Name','??????????','NumberTitle','off');
%subplot(2, 1, 1)
surf(X, Y, -R_sqrt);
title('sqrt');
%subplot(2, 1, 2)
%surf(X, Y, -R_sqrtm);
%title('sqrtm');
R_logm = logm(R1);
R_log = log(R1);
figure('Name','????????','NumberTitle','off');
%subplot(2, 1, 1)
surf(X, Y, -R_log);
title('log');
%subplot(2, 1, 2)
%surf(X, Y, -R_logm);
%title('logm');
R_expm = expm(R1);
R_exp = exp(R1);
figure('Name','??????????','NumberTitle','off');
subplot(1, 2, 1)
surf(X, Y, -R_exp);
title('exp');
subplot(1, 2, 2)
surf(X, Y, -R_expm);
title('expn');
Преобразуем пирамиду R операциями врезки, «отрезав» какой-нибудь из углов.
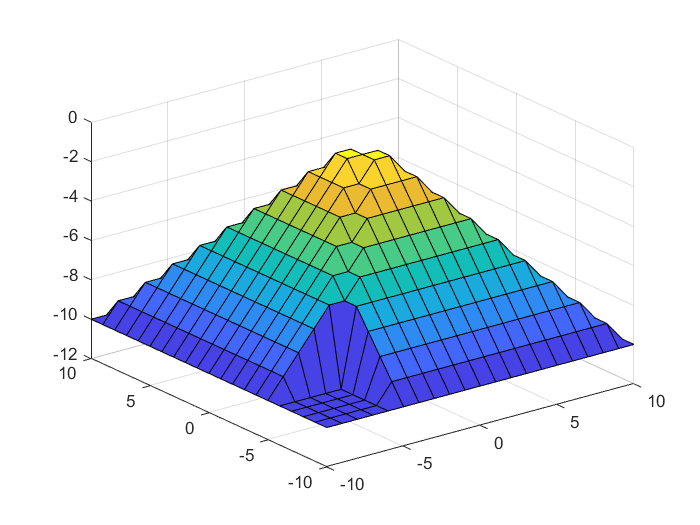
Рис 2 6 Пирамида с отрезанным углом.
Создаем 9 конусов c помощью матрицы 3*3
x = -10:10;
y = ones(1, 21);
X = x'*y;
Y = y'*x;
R = sqrt(X.^2 + Y.^2);
ons = ones(3, 3);
%ons(2, 2) = 0;
R_kron = kron(ons, R);
figure('Name','???????????','NumberTitle','off');
x = -31:31;
y = ones(1, 63);
X = x'*y;
Y = y'*x;
surf(X, Y, -R_kron);
axis
equal
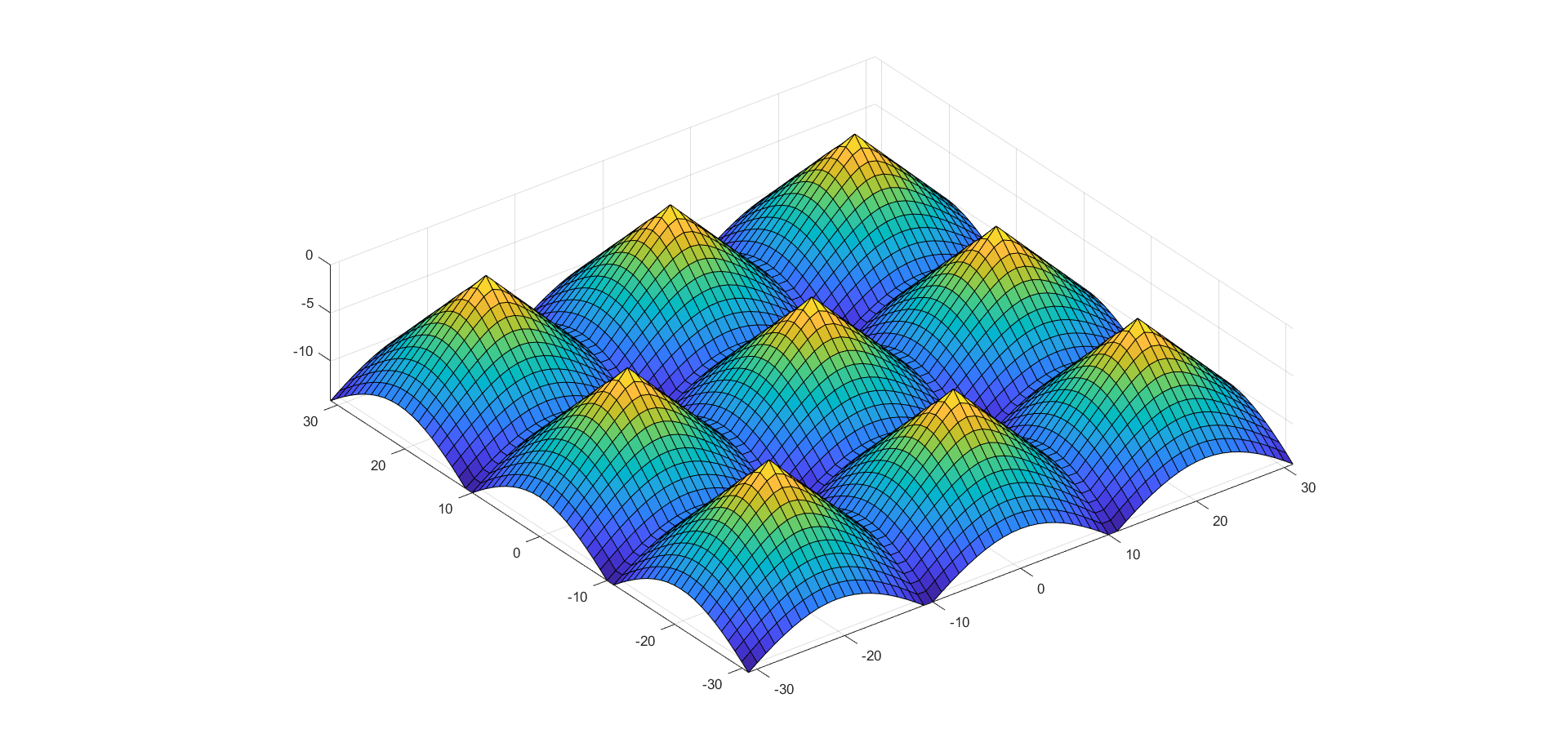
Рис 2.7 Конус, размноженный с помощью тензорного произведения.
Делаем центральный конус в два раза выше соседей.
x1 = -10:10;
y1 = ones(1, 21);
X1 = x1'*y1;
Y1 = y1'*x1;
ons1 = ones(3, 3);
ons1(2, 2) = 0;
R_kron1 = kron(ons1, R);
R2 = sqrt(X1.^2 + Y1.^2);
R2 = 2*R2 - 10*sqrt(2);
ond = [0, 0, 0; 0, 1, 0; 0, 0, 0];
R_kron2 = kron(ond, R2);
figure('Name','??????????','NumberTitle','off');
x1 = -31:31;
y1 = ones(1, 63);
X1 = x1'*y1;
Y1 = y1'*x1;
surf(X1, Y1, -R_kron1-R_kron2);
axis equal

Рис 2.8 Центральный конус увеличен.
Строим тепловые карты на основе графиков из предыдущего пункта.
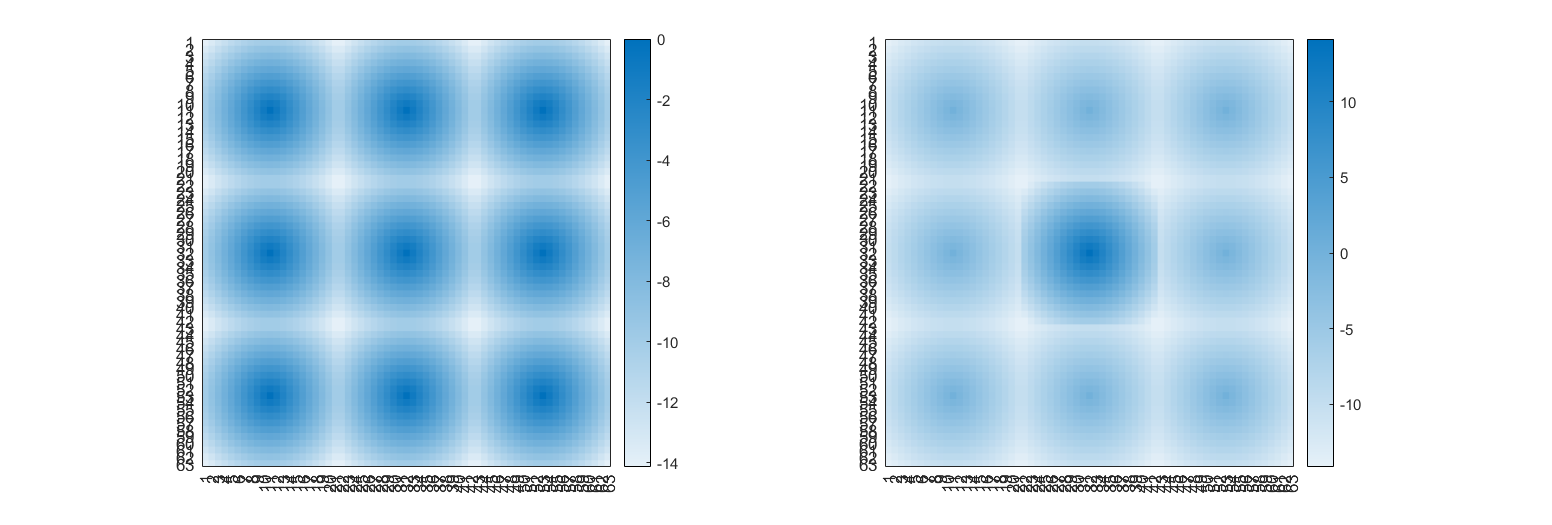
Рис 2.9 Heatmap

Рис 2.10 Imagesc.
figure('Name','heatmap','NumberTitle','off');
subplot(1, 2, 1);
heatmap(-R_kron)
grid off
subplot(1, 2, 2);
heatmap(-R_kron1-R_kron2)
grid off
figure('Name','imagesc','NumberTitle','off');
subplot(1, 2, 1);
imagesc(-R_kron)
grid off
subplot(1, 2, 2);
imagesc(-R_kron1-R_kron2)
grid off
Выводы.
Освоили специфику матричных преобразований MATLAB и сравнительный анализ различных форм графического отображения результатов.
