3. Синтез регуляторов
3.1. ПИ регулятор
()
W4(s) = k4 |
1 + |
1 |
= |
k4(T4s + 1) |
|
T4s |
T4s |
||||
|
|
|
Желаемая характеристика имеет наклон -20 дб/дек вблизи нулевых амплитуд и сов-
падает в низких и высоких частотах с исходной, для сохранения инвариантности и устой-
чивости.
Интегратор исходной системы вносит наклон АЛЧХ -20 дБ/дек, а интегратор регу-
лятора внесет дополнительный наклон (т.е. характеристика в нижних частотах имеет
наклон -40 дБ/дек).
Поскольку нулей у характеристики нет, уменьшить наклон можно только регулято-
ром. Но у него один ноль, соответствущий частоте 1/T4. Таким образом, принципиально
улучшить качество ПИ регулятором не получится.
3.2. ПИД регулятор
Отметим, что классический ПИД-регулятор (ПФ которого приведена выше) никогда не реализуется из-за чрезвычайно высокой чувствительности к шуму. Дифференциру-
ющая часть ПИД-регулятора заменяется на звено вида
W (s) = Ns s + N
где N - коэффициент фильтра. Подобное звено ведет себя как дифференцирующее до частоты ω = N. Если принять N > ω, то на интересующий нас участоа АЧХ подобная замена не повлияет. Поэтому будем искать ПФ ПИД-регулятора в виде
1 |
|
s |
τT4 |
+ T4 |
s2 |
+ T4 + |
1 |
s + 1 |
||||||
|
N |
|||||||||||||
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
) |
|
|
WP ID(s) = k4 (1 + T4s + τN s/N + 1) = k4 ( |
|
T)4s |
1 |
s( |
+ 1 |
|
) |
|||||||
|
N |
|
||||||||||||
При N → ∞ получаем классическую ПФ ПИД-регулятора.
Частота среза исходной системы ωcp ≈ 0.03, а значит нас устроит любое N > 0.03 (с
поправкой на новую частоту среза).
Желаемая передаточная характеристика системы Φwish(s) = Φ(s)WP ID(S) должна иметь такую АЧХ, которая пересекает нуль с наклоном -20 дб/дек, причем чем больше длина отрезка частот с наклоном -20 дб/дек - тем больше запас устойчивости.
9
Для обеспечения подобного поведения системы необходимо получить диполи, кото-
рые "нейтрализуют" неудобные для нас корни ПФ, соответсвующее частотам ω1 = 1/3
иω = 1/30.
Вверхних частотах наклон характеристики будет равняться -40 дб/дек за счет двух интеграторов (первый - от ОУ, второй - от ПИД-регулятора), затем, следует "поднять"
характеристику до -20 дб/дек. Например, это можно сделать, получив в числителе ноль кратности два, равный −1/30. Но чтобы обеспечить наилучший запас устойчивости,
первый нуль следует взять в более низких частотах, а вторым создать диполь.
Пусть длина отрезка с наклоном -20 дб/дек будет примерно 1.5 декады. Есть огра-
ничение в области высоких частот корнем ω2 = 1/3. Тогда следует взять первым корнем числителя ПФ регулятора, например, s = −ωp1 = −1/100, а вторым, s = −ωp2 = −ω1 =
−1/30. В итоге получаем
τT4 + TN4 = T02
1
T4 + N = 2T0
Подставляя выбранные ранее значения
T4 = 150, τ = 26
Это удовлетворяет условиям, описанным в п. 1. Выбрать коэффициент k4 можно про-
извольно. Сделаем это исходя из желаемых показателей качества: перерегулирования
(σ ≤ 10%) и времени регулирования (tp ≤ 50с). Подобным требованиям лучше всего удовлетворяет k4 = 2.76 (найдено эмпирически).
Полученная ЛАЧХ представлена ниже
1.Время регулирования tp = 71.30 c
2.Перерегулирование σ = 4.77%
3.Частота среза ωср = 0.13 рад/с
4.Частота фазового перехода ωпи = 2.22 рад/с
5.Запас по амплитуде ∆L = 40.7 дБ
6.Запас по фазе ∆φ = 66.7◦
Врезультате удалось уменьшить перерегулирование в 5 раз, а время регулирования
в3.
10
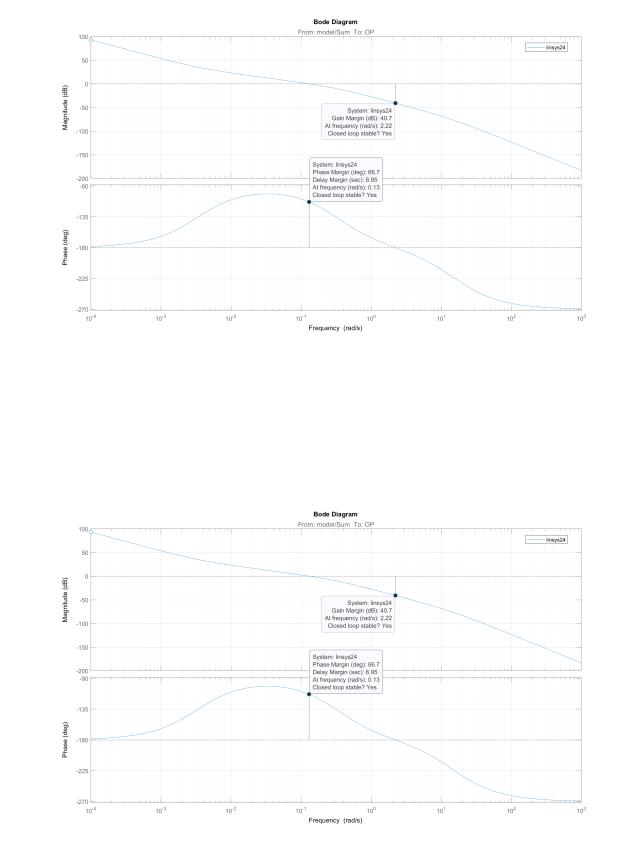
Рис. 3.1. Частотные характеристики с ПИДрегулятором.
Рис. 3.2. Переходная характеристика с ПИД-регудятором.
11
Более того, передаточная функция ПИДрегулятора содержит нулевой полюс. Зна-
чит скорректированная характеристика системы будет обладать астатизмом второго по-
рядка.
|
|
|
|
|
|
|
Wpid(s) = k4 |
T4τs2 + T4s + 1 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
T4s |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Теперь имеем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
Wp k(s) = Wp(s)Wpid(s) |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
eeg |
= lim sΦegG(s) = lim s |
|
1 |
|
|
1 |
= lim |
|
|
|
|
|
1 |
1 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
1 + Wp(s)Wpid(s) s |
|||||||||||||||||
|
|
|
|
s→0 |
|
s→0 |
1 + Wp k(s) s2 |
s→0 |
|
|||||||||||||||||
И окончательно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
eeg = lim sΦegG(s) = lim |
|
|
|
|
s2 |
|
|
|
1 |
= 0 |
(3) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
s2 + W ′ |
(s)W |
′ |
(s) s |
||||||||||||||||||
|
|
|
|
|
s |
→ |
0 |
s |
→ |
0 |
|
|
|
|
||||||||||||
|
W ′(s) |
|
W ′ |
|
|
|
|
|
|
|
p |
|
pid |
|
|
|
|
|
|
|
||||||
где |
и |
- передаточные функции с исключенными интеграторами. Проведя |
||||||||||||||||||||||||
p |
|
pid |
||||||||||||||||||||||||
аналогичные рассуждения для ошибки по возмущению получаем efg = 0.
12