ЛР / Лаб. 2 ТВиМС

Лабораторная работа № 2. Проверка гипотезы о законе распределения генеральной совокупности

Преподаватель: Епихин Валерий Николаевич. Оценка: 5- из 5.

Ошибки: округление должно быть до 2 знаков после запятой.

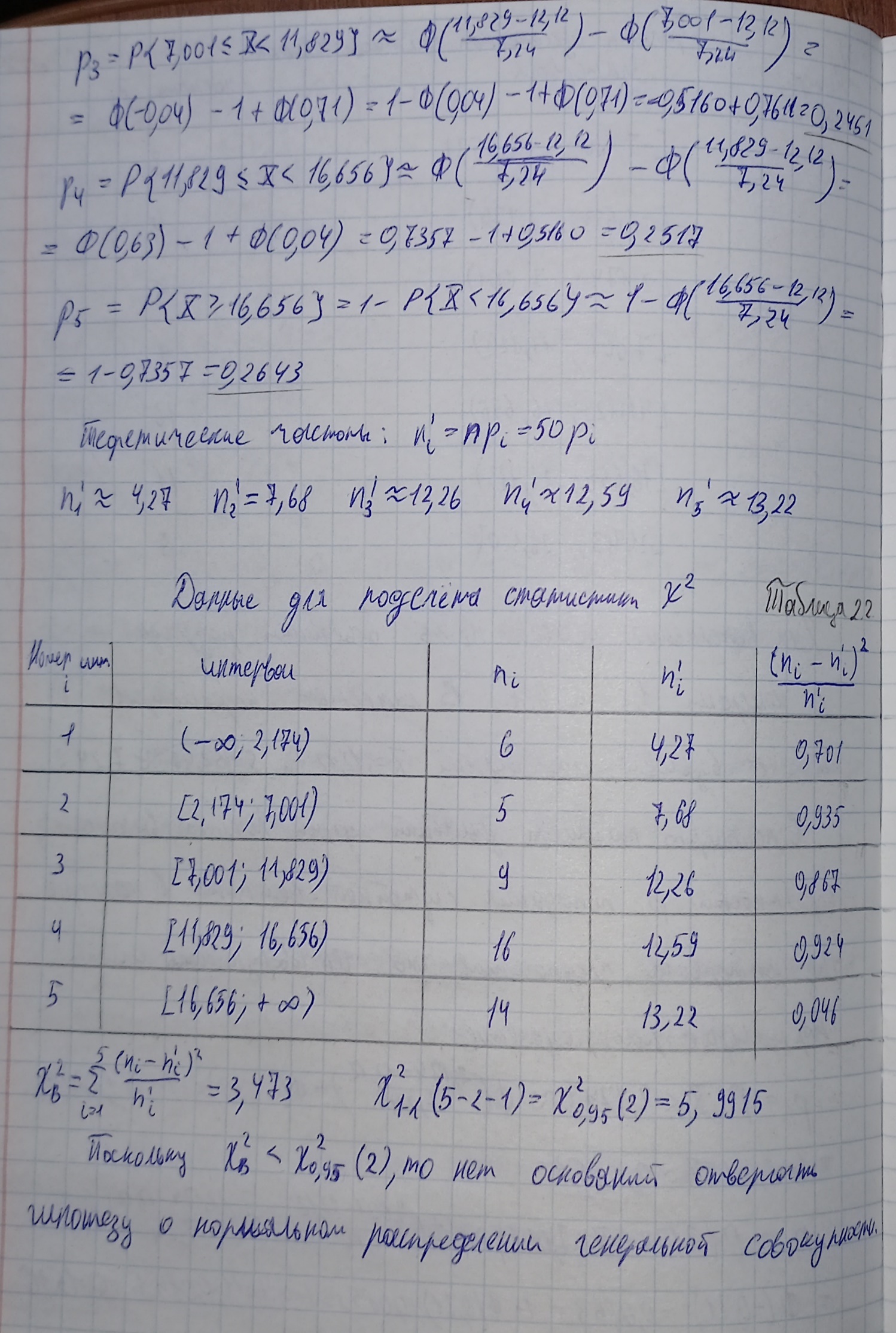
import openpyxl import numpy as np import matplotlib.pyplot as plt import statistics as stat from scipy.stats import t, chi2 def round2(x): return round(x, 2) workbook = openpyxl.load_workbook('BDZ3.xlsx') sheet = workbook['12'] var1 = [] for row in range(2, 52): cell_value = sheet['B' + str(row)].value var1.append(cell_value) #выборка selection = [round2(num) for num in var1] size_selection = len(selection) print(f'Выборка:\n{selection}\n') #вариационный ряд variation_series = sorted(selection) #print(f'Вариационный ряд:\n{variation_series}\n') #размах выборки max_selection = max(selection) min_selection = min(selection) scope = max_selection - min_selection #print(f'Размах выборки:\n{scope}\n') #статистический ряд n = 7 interval_len = scope / n #print(interval_len) interval1 = [min_selection, min_selection + interval_len] interval2 = [interval1[1], interval1[1]] intervals = np.zeros((n, 2)) start = min_selection for i in range(n): end = start + interval_len intervals[i][0] = start intervals[i][1] = end start = end intervals[6][1] = max_selection + 0.01 statistical_series = [] for i in range(n): statistical_series.append([]) for element in variation_series: for i in range(n): if intervals[i][0] <= element < intervals[i][1]: statistical_series[i].append(element) #break #print(f'Статистический ряд:\n{statistical_series}\n') #частоты #print(f'Разряды:\n{intervals}\n') middle_intervals = [] for i in range(n): middle_intervals.append((intervals[i][0] + intervals[i][1])/2) #print(f'Середины разрядов:\n{middle_intervals}\n') frequency = [] for i in range(n): frequency.append(len(statistical_series[i])) #print(f'Частота:\n{frequency}\n') #среднее и дисперсия mx1 = round2(sum(selection)/50) mx2 = 0 for i in range(7): mx2 += middle_intervals[i]*len(statistical_series[i]) mx2_ = mx2/50 mx2 = round2(mx2/50) print(f'Выборочное среднее исходной выборки:\n{mx1}') print(f'Выборочное среднее интервально группированной выборки:\n{mx2}\n') dx11 = 0 for i in range(50): dx11 += (selection[i] - mx1)**2 d1 = dx11 dx11 = d1/50 dx21 = 0 for i in range(7): dx21 += (len(statistical_series[i])*middle_intervals[i]**2) d2 = dx21 dx21 = (d2 - 50*mx2**2)/50 #print(f'Смещённая дисперсия исходной выборки:\n{dx11}') #print(f'Смещённая дисперсия интервально группированной выборки:\n{dx21}\n') dx12 = round2(d1/49) dx22 = round2((d2 - 50*mx2_**2)/49) print(f'Дисперсия исходной выборки:\n{dx12}') print(f'Дисперсия интервально группированной выборки:\n{dx22}\n') #доверительные интервалы p = [0.95, 0.99, 0.9, 0.8, 0.6] a = [round2(1 - i) for i in p] t_list = [round2(t.ppf(1 - a[i]/2, size_selection - 1)) for i in range(len(a))] chi2_list_1 = [round2(chi2.ppf(1 - a[i]/2, size_selection - 1)) for i in range(len(a))] chi2_list_2 = [round2(chi2.ppf(a[i]/2, size_selection - 1)) for i in range(len(a))] def CI_m(x, s2, t_, z): if z == 1: return round2(x - (np.sqrt(s2) * t_) / np.sqrt(size_selection)) if z == 2: return round2(x + (np.sqrt(s2) * t_) / np.sqrt(size_selection)) def CI_chi2(s2, chi2_): return round2((size_selection - 1) * s2 / chi2_) CI_m_selection = {x: [] for x in p} c = 0 for key in p: CI_m_selection[key].append(CI_m(mx1, dx12, t_list[c], 1)) CI_m_selection[key].append(CI_m(mx1, dx12, t_list[c], 2)) c += 1 CI_m_statistical_series = {x: [] for x in p} c = 0 for key in p: CI_m_statistical_series[key].append(CI_m(mx2, dx22, t_list[c], 1)) CI_m_statistical_series[key].append(CI_m(mx2, dx22, t_list[c], 2)) c += 1 print(f'Доверительные интервалы мат. ожидания НЕгруппированной выборки:\n{CI_m_selection}') print(f'Доверительные интервалы мат. ожидания группированной выборки:\n{CI_m_statistical_series}\n') CI_chi2_selection = {x: [] for x in p} c = 0 for key in p: CI_chi2_selection[key].append(CI_chi2(dx12, chi2_list_1[c])) CI_chi2_selection[key].append(CI_chi2(dx12, chi2_list_2[c])) c += 1 CI_chi2_statistical_series = {x: [] for x in p} c = 0 for key in p: CI_chi2_statistical_series[key].append(CI_chi2(dx22, chi2_list_1[c])) CI_chi2_statistical_series[key].append(CI_chi2(dx22, chi2_list_2[c])) c += 1 print(f'Доверительные интервалы дисперсии НЕгруппированной выборки:\n{CI_chi2_selection}') print(f'Доверительные интервалы дисперсии группированной выборки:\n{CI_chi2_statistical_series}\n') #выборочные числовые характеристики from scipy.stats import norm mean, std = norm.fit(selection) print(f"Оценка математического ожидания: {mean:.2f}") print(f"Оценка дисперсии: {std ** 2:.2f}\n") for a_ in a: alpha = a_ mean_ci = t.interval(1 - alpha, len(selection) - 1, loc=mean, scale=std/np.sqrt(len(selection))) std_ci = t.interval(1 - alpha, len(selection) - 1, loc=std, scale=std/np.sqrt(2*(len(selection)-1))) #std_ci = t.interval(1 - alpha, len(selection) - 1, loc=std, scale=std/np.sqrt(2*(len(selection)-1))) print(f"Alpha: {alpha}") print(f"Доверительный интервал для мат. ожидания: [{mean_ci[0]:.2f}, {mean_ci[1]:.2f}]") print(f"Доверительный интервал для дисперсии: [{std_ci[0]**2:.2f}, {std_ci[1]**2:.2f}]\n")

Выборка:

[11.36, 12.17, 10.37, 15.88, 12.96, 21.46, 12.63, 15.16, 2.95, 22.1, 10.86, -2.41, 9.72, 9.76, 16.63, 6.7, -7.48, 19.04, 17.88, 21.32, 12.91, 23.68, 20.53, 2.59, 26.31, 14.87, 19.4, 7.31, 11.06, 15.28, 13.31, 3.42, 9.43, 12.63, 5.91, 13.74, 1.4, 12.25, 19.95, 21.04, -2.02, 13.51, 12.46, 20.28, -3.57, 19.97, 11.61, 16.52, 18.48, 1.5]

Выборочное среднее исходной выборки:

12.3

Выборочное среднее интервально группированной выборки:

12.12

Дисперсия исходной выборки:

58.04

Дисперсия интервально группированной выборки:

52.47

Доверительные интервалы мат. ожидания НЕгруппированной выборки:

{0.95: [10.13, 14.47], 0.99: [9.41, 15.19], 0.9: [10.49, 14.11], 0.8: [10.9, 13.7], 0.6: [11.38, 13.22]}

Доверительные интервалы мат. ожидания группированной выборки:

{0.95: [10.06, 14.18], 0.99: [9.37, 14.87], 0.9: [10.4, 13.84], 0.8: [10.79, 13.45], 0.6: [11.25, 12.99]}

Доверительные интервалы дисперсии НЕгруппированной выборки:

{0.95: [40.5, 90.14], 0.99: [36.35, 104.37], 0.9: [42.87, 83.82], 0.8: [45.84, 77.24], 0.6: [49.82, 70.17]}

Доверительные интервалы дисперсии группированной выборки:

{0.95: [36.61, 81.49], 0.99: [32.87, 94.35], 0.9: [38.76, 75.77], 0.8: [41.44, 69.83], 0.6: [45.04, 63.44]}

Оценка математического ожидания: 12.30

Оценка дисперсии: 56.88

Alpha: 0.05

Доверительный интервал для мат. ожидания: [10.15, 14.44]

Доверительный интервал для дисперсии: [36.13, 82.31]

Alpha: 0.01

Доверительный интервал для мат. ожидания: [9.44, 15.15]

Доверительный интервал для дисперсии: [30.25, 91.84]

Alpha: 0.1

Доверительный интервал для мат. ожидания: [10.51, 14.08]

Доверительный интервал для дисперсии: [39.24, 77.77]

Alpha: 0.2

Доверительный интервал для мат. ожидания: [10.91, 13.68]

Доверительный интервал для дисперсии: [42.93, 72.78]

Alpha: 0.4

Доверительный интервал для мат. ожидания: [11.39, 13.20]

Доверительный интервал для дисперсии: [47.54, 67.05]

Контрольные вопросы

1.

Доверительный интервал:

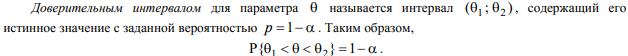
Доверительная вероятность и уровень значимости:

Квантиль – значение, которое заданная случайная величина не превышает с фиксированной вероятностью.

2.

Простые и сложные гипотезы:

Статистическая гипотеза H называется простой, если она однозначно определяет распределение случайной величины X; в противном случае гипотеза H называется сложной. Например, гипотеза о том, что X ~ N(0;1) – простая, а гипотеза о том, что X ~ N(m;1), где m [0; 3], – сложная.

Параметрические или гипотезы о законе распределения:

Если распределение случайной величины X известно и по выборке наблюдений необходимо проверить предположения о значении параметров этого распределения, то такие гипотезы называются параметрическими. Если же по выборке наблюдений необходимо проверить гипотезу о том, что она извлечена из генеральной совокупности X с функцией распределения Fx(x), то такие гипотезы называются гипотезами о законе распределения.

Нулевая и альтернативные гипотезы:

Уровень значимости:

Перед анализом выборки фиксируется некоторая малая вероятность 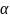, называемая уровнем значимости.

Критическая область:

Пусть W – множество значений статистики Z.

Ошибки первого и второго родов:

Связь с доверительными интервалами:

3.