
ЛР / Лаб. 1 ТВиМС
.docx
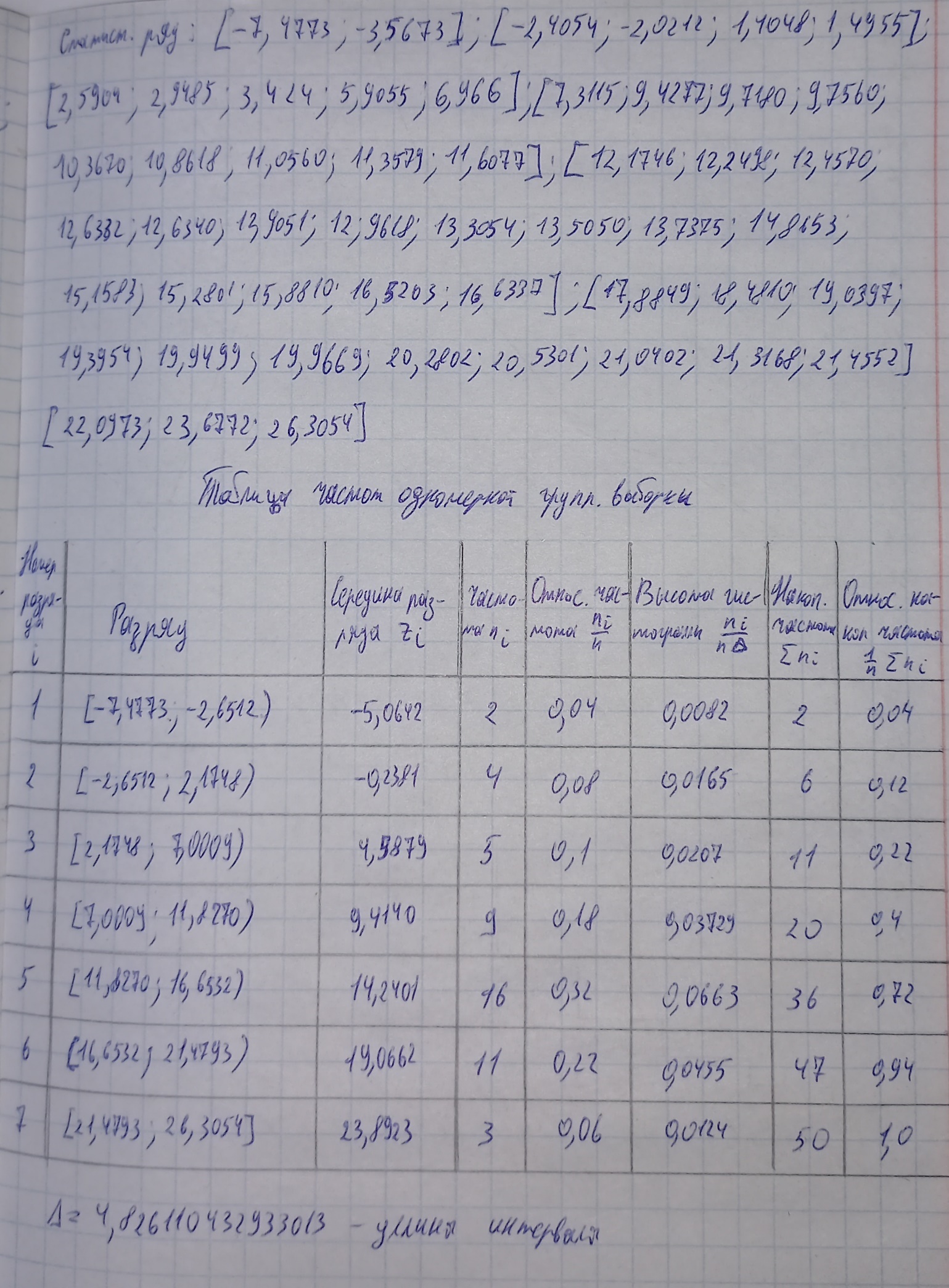
Лабораторная работа № 1. Статистическая обработка одномерной выборки
Преподаватель: Епихин Валерий Николаевич. Оценка: 4 из 5.
Ошибки: округление должно быть до 2 знаков после запятой; не подписаны таблицы и графики.



import openpyxl import numpy as np import matplotlib.pyplot as plt import statistics as stat #[11.357929227788, 12.1746725856113, 10.3670717973447, 15.8810330222863, 12.9618201236958, 21.4552413749681, 12.6322871172341, 15.1583685700916, 2.94858525983582, 22.0973333177357, 10.8618056657188, -2.40546231151357, 9.71801037049916, 9.7560512808964, 16.6337057935906, 6.69669015874598, -7.47734417688979, 19.0397802384291, 17.8849511912566, 21.3168909405277, 12.905196795262, 23.6772261942236, 20.5301197796223, 2.59049674646943, 26.3054288536413, 14.8653143877288, 19.395420972071, 7.31153398117904, 11.0560134668201, 15.2801605638025, 13.3054294533742, 3.4241843328975, 9.42778160650215, 12.634031116373, 5.90554665457665, 13.7375931363223, 1.40480726203896, 12.249863856985, 19.9499514944647, 21.040212257846, -2.02128065794526, 13.5050566256409, 12.4570281955692, 20.280210729993, -3.56734756307764, 19.9669420388534, 11.6077382728375, 16.5203322435901, 18.4810447674934, 1.49557479227326] workbook = openpyxl.load_workbook('BDZ3.xlsx') sheet = workbook['12'] var1 = [] for row in range(2, 52): cell_value = sheet['B' + str(row)].value var1.append(cell_value) #выборка selection = var1 size_selection = len(selection) print(f'Выборка:\n{selection}\n') #вариационный ряд variation_series = sorted(selection) print(f'Вариационный ряд:\n{variation_series}\n') #размах выборки max_selection = max(selection) min_selection = min(selection) scope = max_selection - min_selection print(f'Размах выборки:\n{scope}\n') #статистический ряд n = 7 interval_len = scope / n #print(interval_len) interval1 = [min_selection, min_selection + interval_len] interval2 = [interval1[1], interval1[1]] intervals = np.zeros((n, 2)) start = min_selection for i in range(n): end = start + interval_len intervals[i][0] = start intervals[i][1] = end start = end #intervals[6][1] = max_selection statistical_series = [] for i in range(n): statistical_series.append([]) for element in variation_series: for i in range(n): if intervals[i][0] <= element < intervals[i][1]: statistical_series[i].append(element) #break print(f'Статистический ряд:\n{statistical_series}\n') #частоты print(f'Разряды:\n{intervals}\n') middle_intervals = [] for i in range(n): middle_intervals.append((intervals[i][0] + intervals[i][1])/2) print(f'Середины разрядов:\n{middle_intervals}\n') frequency = [] for i in range(n): frequency.append(len(statistical_series[i])) print(f'Частота:\n{frequency}\n') relative_frequency = [] for i in range(n): relative_frequency.append(frequency[i]/size_selection) print(f'Относительная частота:\n{relative_frequency}\n') height_histogram = [] for i in range(n): height_histogram.append(relative_frequency[i]/interval_len) print(f'Высота гистограммы:\n{height_histogram}\n') accumulated_frequency = [] count = 0 for i in range(n): count += frequency[i] accumulated_frequency.append(count) count = 0 print(f'Накопленная частота:\n{accumulated_frequency}\n') relative_accumulated_frequency = [] for i in range(n): count += frequency[i] relative_accumulated_frequency.append(count/size_selection) count = 0 print(f'Относительная накопленная частота:\n{relative_accumulated_frequency}\n') frequency_interval_len = frequency.copy() for i in range(n): frequency_interval_len[i] = frequency_interval_len[i]/interval_len plt.subplot(1,2,1) plt.bar(middle_intervals, frequency_interval_len, interval_len, color='green', edgecolor='black', linewidth=1.5) plt.plot(middle_intervals, frequency_interval_len, color='black') plt.xticks(middle_intervals, [f"{x:.2f}" for x in middle_intervals]) plt.yticks(np.arange(0, max(frequency_interval_len) + 0.2, 0.2)) plt.xlabel('x') plt.ylabel('ni/d') plt.title('Гистограмма и полигон частот') plt.grid() #b = np.linspace(middle_intervals[0], middle_intervals[-1], num=len(middle_intervals)) #print(b) #plt.xticks(b + interval_len/2, str(middle_intervals)) #plt.subplot(1,2,2) #plt.bar(middle_intervals, height_histogram, interval_len, color='green', # edgecolor='black', linewidth=1.5) #plt.xticks(middle_intervals, [f"{x:.2f}" for x in middle_intervals]) #plt.xlabel('x') #plt.ylabel('ni/nd') #plt.title('Гистограмма относительных частот с наложением графика теоретической функции плотности вероятности') #plt.grid() plt.subplot(1,2,2) for i in range(n): plt.plot([intervals[i][0], intervals[i][1]], [relative_accumulated_frequency[i], relative_accumulated_frequency[i]], color='black') for i in range(n-1): plt.plot([intervals[i][1], intervals[i][1]], [relative_accumulated_frequency[i], relative_accumulated_frequency[i+1]], color='black') # plt.plot([intervals[0][0], intervals[0][0]], # [0, relative_accumulated_frequency[0]], color='black') # plt.plot([intervals[0][0] - 3, intervals[0][0]], # [0, 0], color='black') plt.xticks(np.arange(-8, 28, 2)) plt.yticks(np.arange(0, 1 + 0.1, 0.1)) #plt.step(intervals, relative_accumulated_frequency) #plt.step(selection, relative_accumulated_frequency) plt.xlabel('x') plt.ylabel('Fx') plt.title('Эмпирическая функция распределения') plt.grid() # mode_selection = stat.mode(selection) # mode_variation_series = stat.mode(variation_series) # print(f'Мода исходной выборки:\n{mode_selection}') # print(f'Мода интервально группированной выборки:\n{mode_variation_series}\n') # # median_selection = stat.median(selection) # median_variation_series = stat.median(variation_series) # print(f'Медиана исходной выборки:\n{median_selection}') # print(f'Медиана интервально группированной выборки:\n{median_variation_series}\n') # # mean_selection = stat.mean(selection) # mean_variation_series = stat.mean(variation_series) # print(f'Выборочное среднее исходной выборки:\n{mean_selection}') # print(f'Выборочное среднее интервально группированной выборки:\n{mean_variation_series}\n') # # variance_selection = stat.variance(selection) # variance_variation_series = stat.variance(variation_series) # print(f'Дисперсия исходной выборки:\n{variance_selection}') # print(f'Дисперсия интервально группированной выборки:\n{variance_variation_series}\n') # # pvariance_selection = stat.pvariance(selection) # pvariance_variation_series = stat.pvariance(variation_series) # print(f'Смещённая дисперсия исходной выборки:\n{pvariance_selection}') # print(f'Смещённая дисперсия интервально группированной выборки:\n{pvariance_variation_series}\n') mx1 = sum(selection)/50 mx2 = 0 for i in range(7): mx2 += middle_intervals[i]*len(statistical_series[i]) mx2 = mx2/50 print(f'Выборочное среднее исходной выборки:\n{mx1}') print(f'Выборочное среднее интервально группированной выборки:\n{mx2}\n') dx11 = 0 for i in range(50): dx11 += (selection[i] - mx1)**2 d1 = dx11 dx11 = d1/50 dx21 = 0 for i in range(7): dx21 += (len(statistical_series[i])*middle_intervals[i]**2) d2 = dx21 dx21 = (d2 - 50*mx2**2)/50 print(f'Смещённая дисперсия исходной выборки:\n{dx11}') print(f'Смещённая дисперсия интервально группированной выборки:\n{dx21}\n') dx12 = d1/49 dx22 = (d2 - 50*mx2**2)/49 print(f'Дисперсия исходной выборки:\n{dx12}') print(f'Дисперсия интервально группированной выборки:\n{dx22}\n') h1 = (variation_series[24] + variation_series[25])/2 h2 = intervals[int(7/2)][0] + interval_len*((size_selection/2 - sum(frequency[0:int(7/2)]))/frequency[int(7/2)]) print(f'Медиана исходной выборки:\n{h1}') print(f'Медиана интервально группированной выборки:\n{h2}\n') d1 = stat.mode(selection) i_ = 0 for i in range(len(frequency) - 1): if frequency[i] < frequency[i+1]: i_ = i+1 ad = intervals[i_][0] d2 = ad + interval_len*((frequency[i_] - frequency[i_-1])/(2*frequency[i_] - frequency[i_-1] - frequency[i_+1])) print(f'Мода исходной выборки:\n{d1}') print(f'Мода интервально группированной выборки:\n{d2}') plt.show()
Выборка:
[11.357929227788, 12.1746725856113, 10.3670717973447, 15.8810330222863, 12.9618201236958, 21.4552413749681, 12.6322871172341, 15.1583685700916, 2.94858525983582, 22.0973333177357, 10.8618056657188, -2.40546231151357, 9.71801037049916, 9.7560512808964, 16.6337057935906, 6.69669015874598, -7.47734417688979, 19.0397802384291, 17.8849511912566, 21.3168909405277, 12.905196795262, 23.6772261942236, 20.5301197796223, 2.59049674646943, 26.3054288536413, 14.8653143877288, 19.395420972071, 7.31153398117904, 11.0560134668201, 15.2801605638025, 13.3054294533742, 3.4241843328975, 9.42778160650215, 12.634031116373, 5.90554665457665, 13.7375931363223, 1.40480726203896, 12.249863856985, 19.9499514944647, 21.040212257846, -2.02128065794526, 13.5050566256409, 12.4570281955692, 20.280210729993, -3.56734756307764, 19.9669420388534, 11.6077382728375, 16.5203322435901, 18.4810447674934, 1.49557479227326]
Вариационный ряд:
[-7.47734417688979, -3.56734756307764, -2.40546231151357, -2.02128065794526, 1.40480726203896, 1.49557479227326, 2.59049674646943, 2.94858525983582, 3.4241843328975, 5.90554665457665, 6.69669015874598, 7.31153398117904, 9.42778160650215, 9.71801037049916, 9.7560512808964, 10.3670717973447, 10.8618056657188, 11.0560134668201, 11.357929227788, 11.6077382728375, 12.1746725856113, 12.249863856985, 12.4570281955692, 12.6322871172341, 12.634031116373, 12.905196795262, 12.9618201236958, 13.3054294533742, 13.5050566256409, 13.7375931363223, 14.8653143877288, 15.1583685700916, 15.2801605638025, 15.8810330222863, 16.5203322435901, 16.6337057935906, 17.8849511912566, 18.4810447674934, 19.0397802384291, 19.395420972071, 19.9499514944647, 19.9669420388534, 20.280210729993, 20.5301197796223, 21.040212257846, 21.3168909405277, 21.4552413749681, 22.0973333177357, 23.6772261942236, 26.3054288536413]
Размах выборки:
33.78277303053109
Статистический ряд:
[[-7.47734417688979, -3.56734756307764], [-2.40546231151357, -2.02128065794526, 1.40480726203896, 1.49557479227326], [2.59049674646943, 2.94858525983582, 3.4241843328975, 5.90554665457665, 6.69669015874598], [7.31153398117904, 9.42778160650215, 9.71801037049916, 9.7560512808964, 10.3670717973447, 10.8618056657188, 11.0560134668201, 11.357929227788, 11.6077382728375], [12.1746725856113, 12.249863856985, 12.4570281955692, 12.6322871172341, 12.634031116373, 12.905196795262, 12.9618201236958, 13.3054294533742, 13.5050566256409, 13.7375931363223, 14.8653143877288, 15.1583685700916, 15.2801605638025, 15.8810330222863, 16.5203322435901, 16.6337057935906], [17.8849511912566, 18.4810447674934, 19.0397802384291, 19.395420972071, 19.9499514944647, 19.9669420388534, 20.280210729993, 20.5301197796223, 21.040212257846, 21.3168909405277, 21.4552413749681], [22.0973333177357, 23.6772261942236, 26.3054288536413]]
Разряды:
[[-7.47734418 -2.65123374]
[-2.65123374 2.17487669]
[ 2.17487669 7.00098712]
[ 7.00098712 11.82709755]
[11.82709755 16.65320799]
[16.65320799 21.47931842]
[21.47931842 26.30542885]]
Середины разрядов:
[-5.0642889604232835, -0.23817852749027102, 4.587931905442742, 9.414042338375754, 14.240152771308768, 19.066263204241782, 23.892373637174796]
Частота:
[2, 4, 5, 9, 16, 11, 3]
Относительная частота:
[0.04, 0.08, 0.1, 0.18, 0.32, 0.22, 0.06]
Высота гистограммы:
[0.008288247970258414, 0.016576495940516828, 0.020720619925646035, 0.03729711586616286, 0.06630598376206731, 0.045585363836421276, 0.01243237195538762]
Накопленная частота:
[2, 6, 11, 20, 36, 47, 50]
Относительная накопленная частота:
[0.04, 0.12, 0.22, 0.4, 0.72, 0.94, 1.0]
Выборочное среднее исходной выборки:
12.295620678105616
Выборочное среднее интервально группированной выборки:
12.116664180818242
Смещённая дисперсия исходной выборки:
56.862367413634665
Смещённая дисперсия интервально группированной выборки:
51.390016792132265
Дисперсия исходной выборки:
58.02282389146394
Дисперсия интервально группированной выборки:
52.438792645032926
Медиана исходной выборки:
12.769613955817501
Медиана интервально группированной выборки:
14.508270017582824
Мода исходной выборки:
11.357929227788
Мода интервально группированной выборки:
14.642328640719853
Контрольные вопросы
Вариационный ряд - выборка объёма n из генеральной совокупности X, упорядоченная по неубыванию своих элементов.
Статистический ряд - таблица, которая в
первой строке содержит значения выборки, во второй
строке – частоты, а в третьей строке – относительные частоты этих значений.
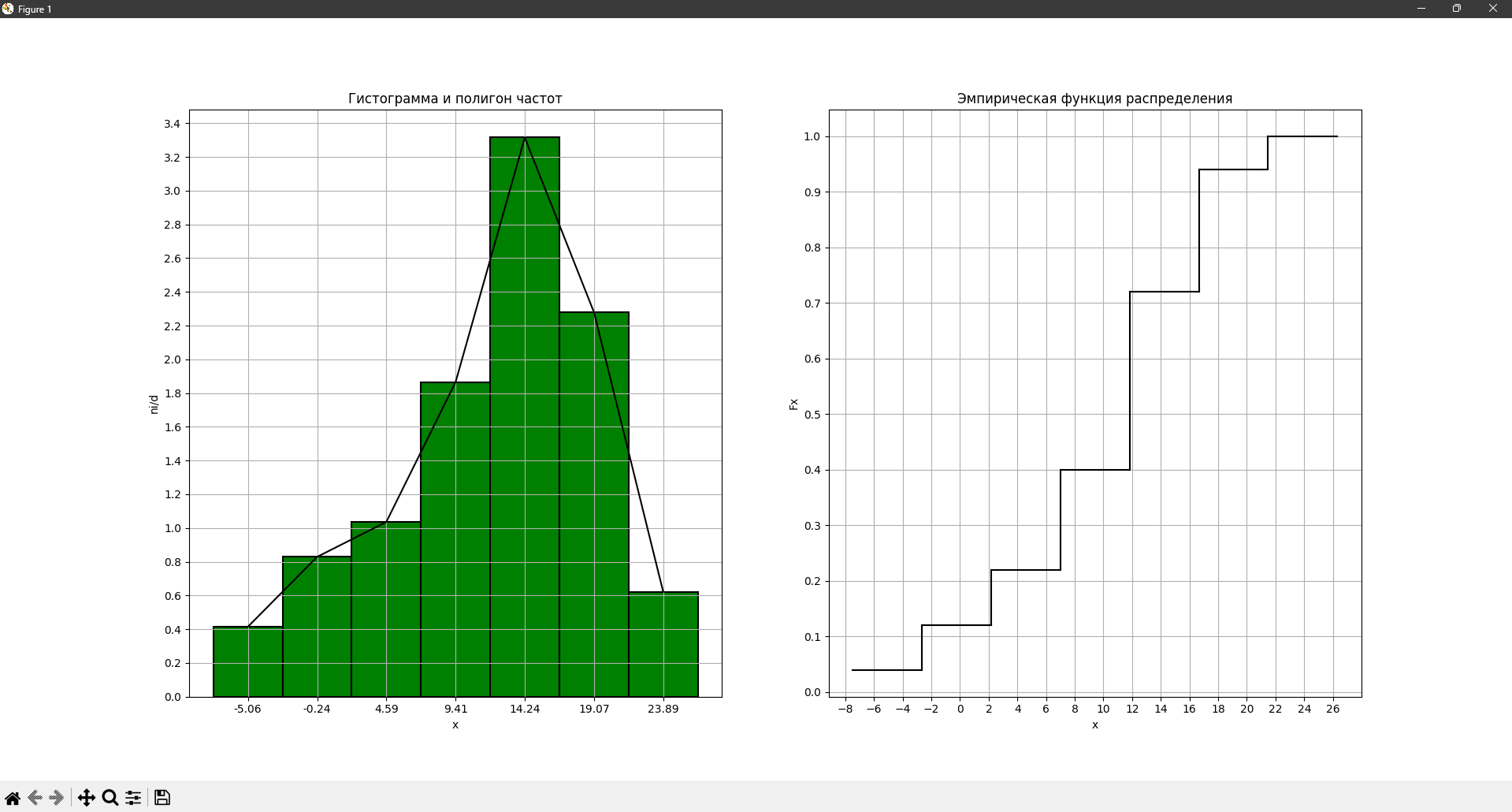
Гистограмма частот:

Полигон частот - ломаная, звенья которой соединяют середины горизонтальных отрезков, ограничивающих гистограмму частот сверху.
Эмпирическая функция распределения:

Выборочные числовые характеристики негруппированной выборки:
Математическое ожидание (среднее):

Дисперсия:

Мода - элемент выборки, встречающийся с наибольшей частотой.
Медиана - называется число, которое делит вариационный ряд на две части, содержащие равное число элементов.
Выборочные числовые характеристики группированной выборки
Математическое ожидание (среднее):
![]()
Дисперсия:

Мода:

Медиана:

