
Лабы (Смирнова) / Лабораторная ТВИМС №2 (Вариант 28)
.docxМИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ
Ордена Трудового Красного Знамени
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский технический университет связи и информатики»
Кафедра «Теория вероятности и прикладная математика»
Лабораторная работа №2
по дисциплине Теория вероятностей и математическая статистика
на тему
«Проверка статистических гипотез и теория оценивания»
Вариант 28
Выполнил: студент гр. БББ0000 Фамилия И.О.
Проверила: доцент кафедры «Теория вероятности и прикладная математика»
Смирнова Н.И.
Москва 2023г.
1. Задание
Задание 1
С помощью критериев согласия Пирсона и Колмогорова проверить гипотезу о том, что выборка из задания 2 лабораторной работы 1 имеет нормальное распределение.
Задание 2
Для выборки из задания 2 лабораторной работы 1 найти интервальные оценки параметров нормального распределения.
Дан коэффициент сменности оборудования 30-ти предприятий:
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
1,25 |
1,13 |
1,10 |
1,15 |
1,23 |
1,39 |
1,38 |
1,35 |
1,42 |
1,37 |
1,41 |
1,35 |
1,48 |
1,24 |
1,40 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
1,45 |
1,40 |
1,28 |
1,33 |
1,22 |
1,28 |
1,47 |
1,27 |
1,51 |
1,46 |
1,27 |
1,43 |
1,50 |
1,35 |
1,41 |
2. Результаты вычислений
Задание 1. Решение.
Дан коэффициент сменности оборудования 30-ти предприятий.
Проверим гипотезу при уровне значимости α = 0,01.
Вариационный ряд (n = 30):
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
1,1 |
1,13 |
1,15 |
1,22 |
1,23 |
1,24 |
1,25 |
1,27 |
1,27 |
1,28 |
1,28 |
1,33 |
1,35 |
1,35 |
1,35 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
1,37 |
1,38 |
1,39 |
1,4 |
1,4 |
1,41 |
1,41 |
1,42 |
1,43 |
1,45 |
1,46 |
1,47 |
1,48 |
1,5 |
1,51 |
|
[1,07;1,14) |
[1,14;1,21) |
[1,21;1,28) |
[1,28;1,35) |
[1,35;1,42) |
[1,42;1,51) |
|
2 |
1 |
6 |
3 |
10 |
8 |
|
0,07 |
0,03 |
0,2 |
0,1 |
0,33 |
0,27 |
|
1 |
0,43 |
2,86 |
1,43 |
4,71 |
3,86 |
|
1,11 |
1,18 |
1,25 |
1,32 |
1,39 |
1,47 |
Заметим, что число наблюдений в 1-ом, 2-ом и 4-ом интервалах меньше 5, поэтому объединим их с соседними.
Получим следующий статистический ряд:
|
[1,07; 1,35) |
[1,35;1,42) |
[1,42;1,51) |
|
12 |
10 |
8 |
|
0,4 |
0,33 |
0,27 |
|
1,21 |
1,39 |
1,47 |
С.в. – отклонение – обозначим
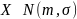
Для подсчета статистики критерия
 найдем теоретические
найдем теоретические
частоты:






p1 = P(-

 p2
= P(
p2
= P(

p3 = P(1,42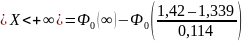
 ;
;
|
[- |
[1,35;1,42) |
[1,42; + ) |
|
12 |
10 |
8 |
|
16,194 |
7,713 |
7,167 |

Находим число степеней свободы. Параметра 2, значит r = 2. Количество интервалов – 3, значит m = 3. Следовательно, k = 3 - 2 – 1 = 0;
|
[1,07;1,25) |
[1,25;1,35) |
[1,35;1,42) |
[1,42;1,51) |
|
6 |
6 |
10 |
8 |
|
|
|
0,33 |
0,27 |
|
|
|
1,39 |
1,47 |
Задание 2. Решение.
Выборка непрерывной генеральной совокупности, содержащая показатели работы предприятий:
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
1,25 |
1,13 |
1,10 |
1,15 |
1,23 |
1,39 |
1,38 |
1,35 |
1,42 |
1,37 |
1,41 |
1,35 |
1,48 |
1,24 |
1,40 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
1,45 |
1,40 |
1,28 |
1,33 |
1,22 |
1,28 |
1,47 |
1,27 |
1,51 |
1,46 |
1,27 |
1,43 |
1,50 |
1,35 |
1,41 |
Объём выборки n = 30.
 1,1;
1,1;
 ,
следовательно, интервал варьирования
[
,
следовательно, интервал варьирования
[ ]:
]:
[1,1; 1,51], размах выборки R
= ( )
= 1,51 - 1,1= 0,41.
)
= 1,51 - 1,1= 0,41.
Проранжируем данные, построим вариационный ряд:
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
1,1 |
1,13 |
1,15 |
1,22 |
1,23 |
1,24 |
1,25 |
1,27 |
1,27 |
1,28 |
1,28 |
1,33 |
1,35 |
1,35 |
1,35 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
1,37 |
1,38 |
1,39 |
1,4 |
1,4 |
1,41 |
1,41 |
1,42 |
1,43 |
1,45 |
1,46 |
1,47 |
1,48 |
1,5 |
1,51 |
Выполним группировку данных:
Число интервалов m =

Величина
интервала разбиения: h =
 0,07
0,07
Начало
первого интервала:
 1,07
1,07
– центр i-го интервала.
|
[1,07;1,14) |
[1,14;1,21) |
[1,21;1,28) |
[1,28;1,35) |
[1,35;1,42) |
[1,42;1,51) |
|
2 |
1 |
6 |
3 |
10 |
8 |
|
0,07 |
0,03 |
0,2 |
0,1 |
0,33 |
0,27 |
|
1 |
0,43 |
2,86 |
1,43 |
4,71 |
3,86 |
|
1,11 |
1,18 |
1,25 |
1,32 |
1,39 |
1,47 |
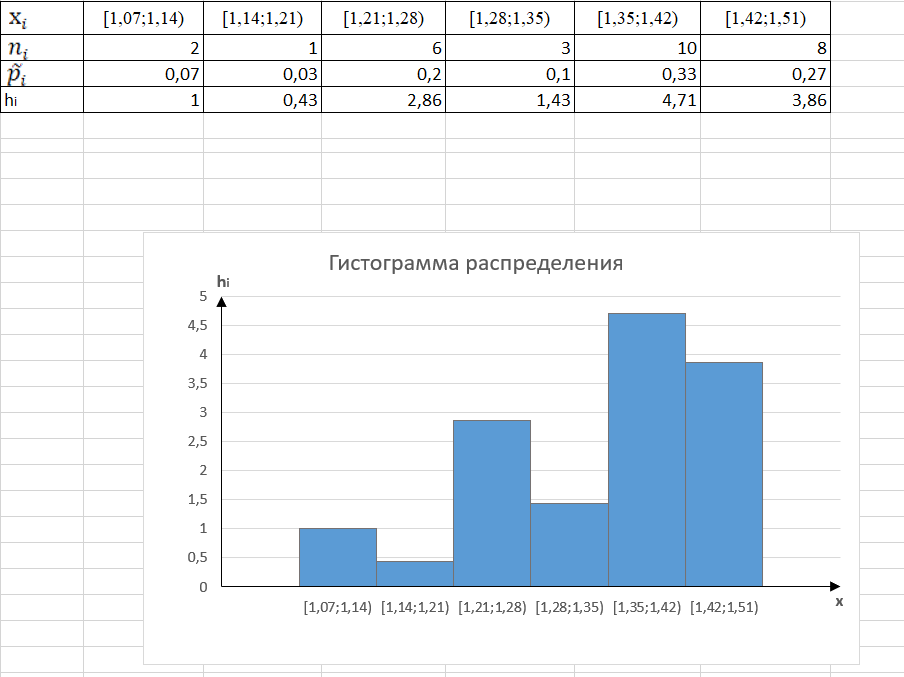
Построим гистограмму распределения:

Эмпирическая функция распределения:
 (x)
=
(x)
=

Построим график эмпирической функции распределения:
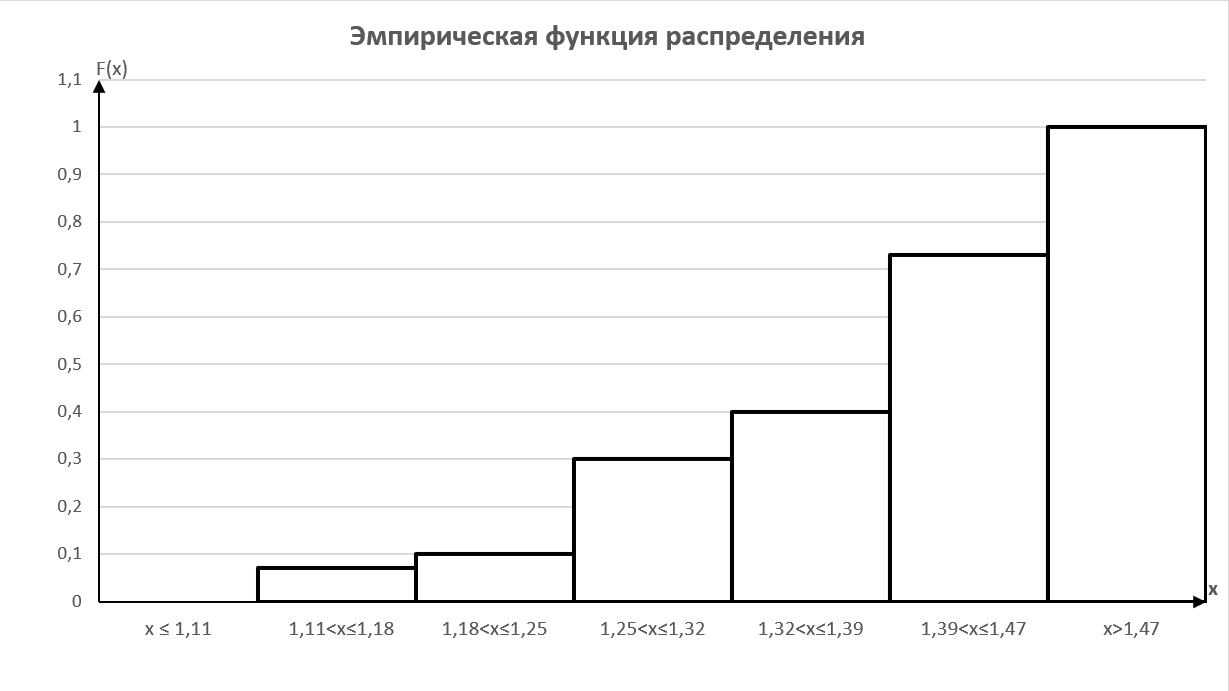
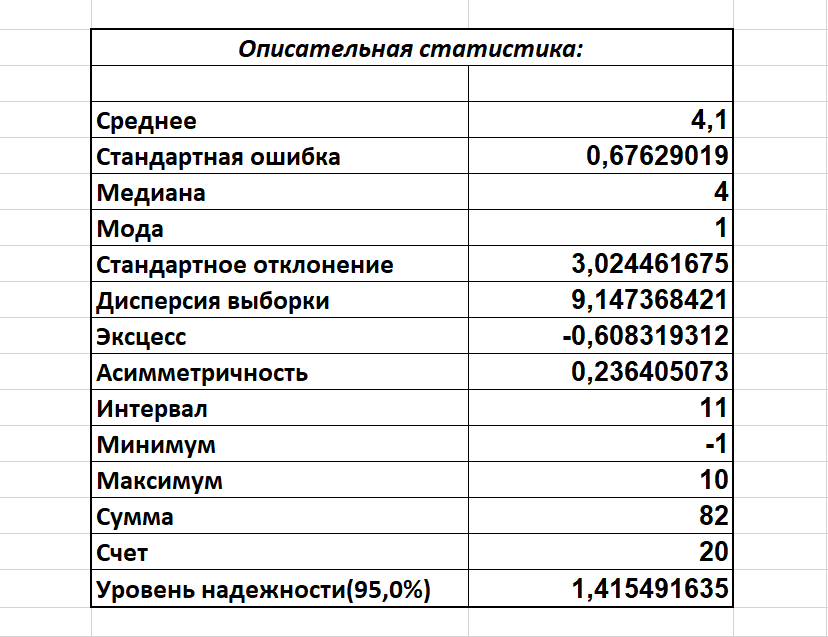
Вычислим основные описательные статистики.
Выборочное среднее:
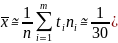
 1,35
Выборочная
смещенная дисперсия:
1,35
Выборочная
смещенная дисперсия:


Выборочная несмещенная (исправленная) дисперсия:
 0,0134
0,0134
Среднеквадратическое отклонение:
 0,114
0,114
 0,116
0,116
Выборочная мода:
 [1,35;1,42)
[1,35;1,42)
Выборочная медиана:

Нижняя квартиль:
 1,27
1,27
Верхняя квартиль:
 1,42
1,42
Интерквартильный размах:
Iqr
=

«Усы» для «ящика с усами»:


Построим
«ящик с усами» (т.к. выбросов нет – строим
по
 и
и
 ):
):

3. Результаты выполнения вычислений в Excel

Задание 1.



Задание 2.



4. Выводы
В данной работе я научился по представленным выборкам дискретной и непрерывной генеральных совокупностей строить вариационный ряд, находить интервал варьирования и размах, выполнять группировку данных, находить выборочное среднее, смещенную и несмещенную дисперсию, среднеквадратическое отклонение, моду, выборочную медиану, нижнюю и верхнюю квартиль. Строить полигон частот, гистограмму распределения, график эмпирической функции распределения и «ящик с усами».





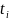
 ;
1,35)
;
1,35)