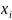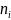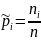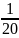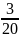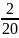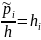МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ

Ордена Трудового Красного Знамени

Федеральное государственное бюджетное образовательное учреждение высшего образования

«Московский технический университет связи и информатики»

Кафедра «Теория вероятности и прикладная математика»

Лабораторная работа №1

по дисциплине Теория вероятностей и математическая статистика

на тему

«Описательная статистика»

Вариант 28

Выполнил: студент гр. БББ0000 Фамилия И.О.

Проверила: доцент кафедры «Теория вероятности и прикладная математика»

Смирнова Н.И.

Москва 2023г.

1. Задание

Задание 1

По предложенной выборке дискретной генеральной совокупности, содержащей рейтинг группы студентов, построить вариационный ряд, найти объем выборки, интервал варьирования, размах выборки, построить статистический ряд распределения, эмпирическую функцию распределений, вычислить основные описательные статистики: выборочное среднее, выборочные смещенную и несмещенную дисперсию и среднеквадратическое отклонение, выборочную моду, выборочную медиану, нижнюю и верхнюю квартиль. Построить полигон частот, график эмпирической функции распределения и «ящик с усами».

Задание 1. Дана выборка 1 4 5 -1 2 4 0 6 8 10 5 7 5 1 9 1 2 6 4 3

Задание 2

По предложенной выборке непрерывной генеральной совокупности, содержащей показатели работы предприятий, построить вариационный ряд, найти объем выборки, интервал варьирования, размах выборки, выполнить группировку данных, построить гистограмму распределения, эмпирическую функцию распределения, вычислить основные описательные статистики: выборочное среднее, выборочные смещенную и несмещенную дисперсию и среднеквадратическое отклонение, выборочную моду, по не группированным данным найти выборочную медиану, нижнюю и верхнюю квартиль. Построить гистограмму, график эмпирической функции распределения и «ящик с усами».

Задание 2. Дан коэффициент сменности оборудования 30-ти предприятий:

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1,25	1,13	1,10	1,15	1,23	1,39	1,38	1,35	1,42	1,37	1,41	1,35	1,48	1,24	1,40
16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
1,45	1,40	1,28	1,33	1,22	1,28	1,47	1,27	1,51	1,46	1,27	1,43	1,50	1,35	1,41

2. Результаты вычислений

Задание 1. Решение.

Рейтинг группы студентов - выборка дискретной генеральной совокупности:

1 4 5 -1 2 4 0 6 8 10 5 7 5 1 9 1 2 6 4 3.

Здесь каждое 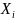– рейтинг студента группы, i = 1, 2, …, n.

Объём выборки n = 20.

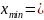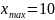-1, , следовательно, интервал варьирования [ ]:

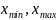[-1, 10], размах выборки R = (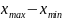 ) = 10 - (-1) = 11.

Ранжируем выборку и построим вариационный ряд ( ):

(-1, 0, 1, 1, 1, 2, 2, 3, 4, 4, 4, 5, 5, 5, 6, 6, 7, 8, 9, 10).

Число наблюдаемых явлений (элементов выборки) невелико и с.в. является дискретной – значит, группировка данных не требуется.

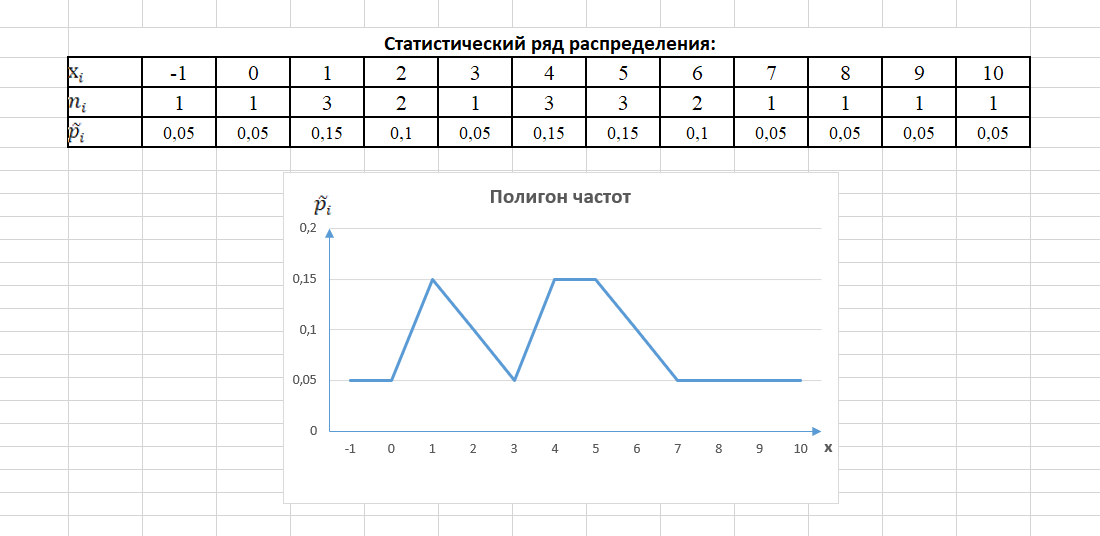
Составим статистический ряд распределения:

	-1	0	1	2	3	4	5	6	7	8	9	10
	1	1	3	2	1	3	3	2	1	1	1	1
	0,05	0,05	0,15	0,1	0,05	0,15	0,15	0,1	0,05	0,05	0,05	0,05

– частоты значений , – относительные частоты- статистические вероятности.

Построим графическое изображение статистического ряда – полигон частот:

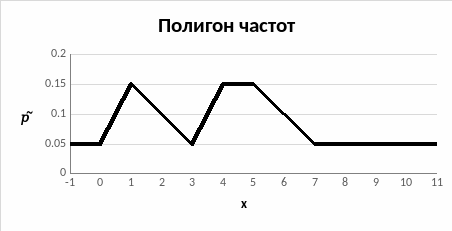
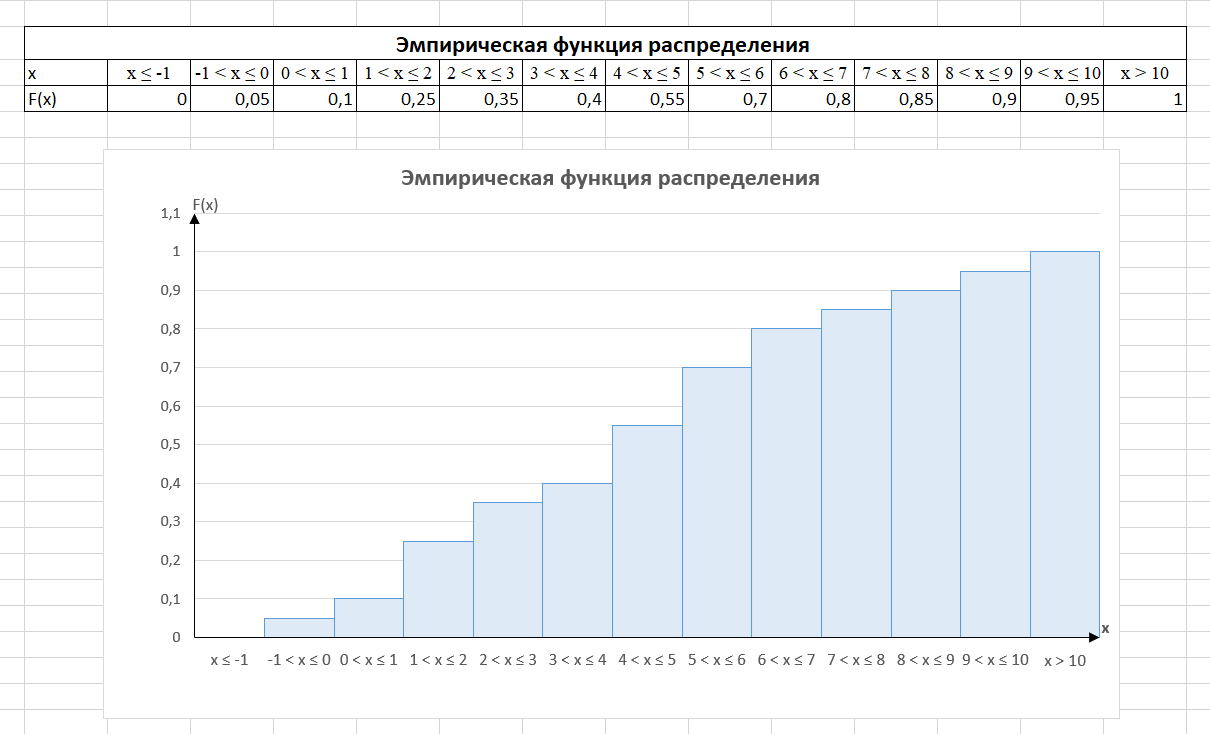
Эмпирическая функция распределения 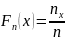(где 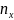– число элементов < x):

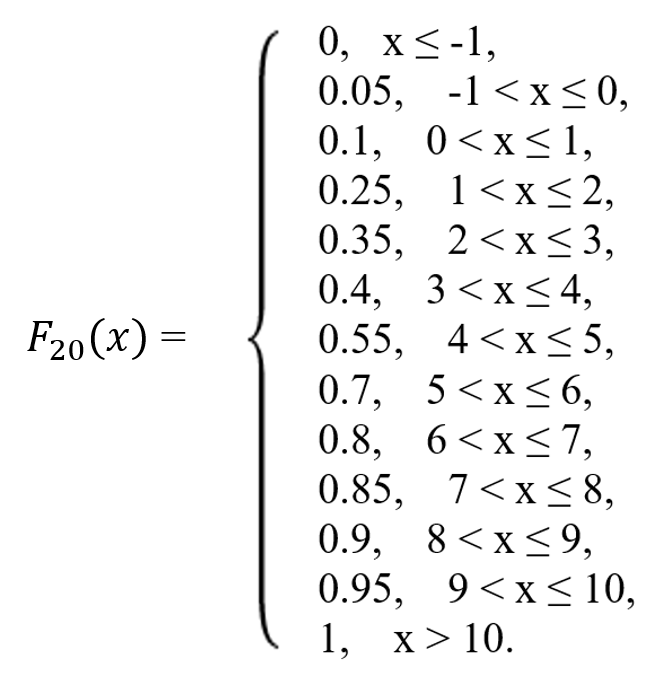
Построим график эмпирической функции распределения:

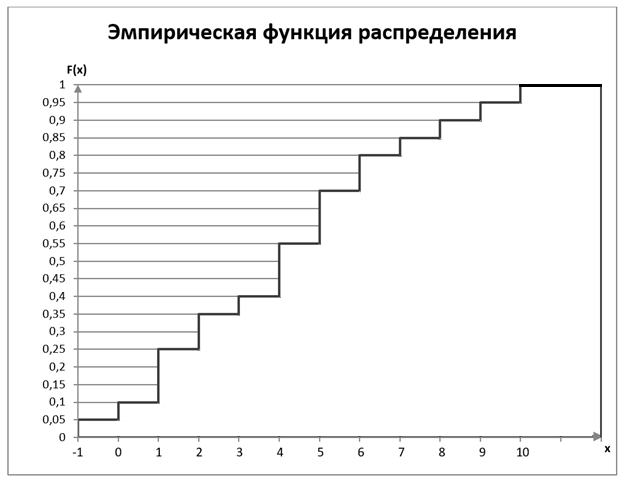
Вычислим основные описательные статистики.

Выборочное среднее:

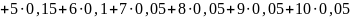= 4,1 Выборочная смещенная дисперсия:

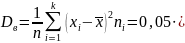
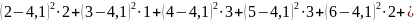
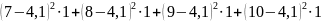= 8,69

Выборочная несмещенная (исправленная) дисперсия:

9,1474

Среднеквадратическое отклонение:

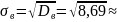2,9479

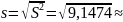3,0245

Выборочная мода, так как наиболее встречающихся значений в выборке несколько, равна первому из них:

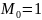
Выборочная медиана:

Нижняя квартиль:

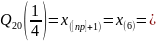2

Верхняя квартиль:

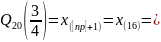6

Интерквартильный размах:

Iqr =

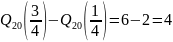
«Усы» для «ящика с усами»:

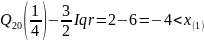
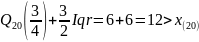
Построим «ящик с усами» (т.к. выбросов нет – строим по 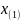и ):

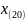Задание 2. Решение.

Выборка непрерывной генеральной совокупности, содержащая показатели работы предприятий:

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1,25	1,13	1,10	1,15	1,23	1,39	1,38	1,35	1,42	1,37	1,41	1,35	1,48	1,24	1,40
16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
1,45	1,40	1,28	1,33	1,22	1,28	1,47	1,27	1,51	1,46	1,27	1,43	1,50	1,35	1,41

Объём выборки n = 30.

1,1; 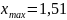, следовательно, интервал варьирования [ ]:

[1,1; 1,51], размах выборки R = ( ) = 1,51 - 1,1= 0,41.

Проранжируем данные, построим вариационный ряд:

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1,1	1,13	1,15	1,22	1,23	1,24	1,25	1,27	1,27	1,28	1,28	1,33	1,35	1,35	1,35
16	17	18	19	20	21	22	23	24	25	26	27	28	29	30
1,37	1,38	1,39	1,4	1,4	1,41	1,41	1,42	1,43	1,45	1,46	1,47	1,48	1,5	1,51

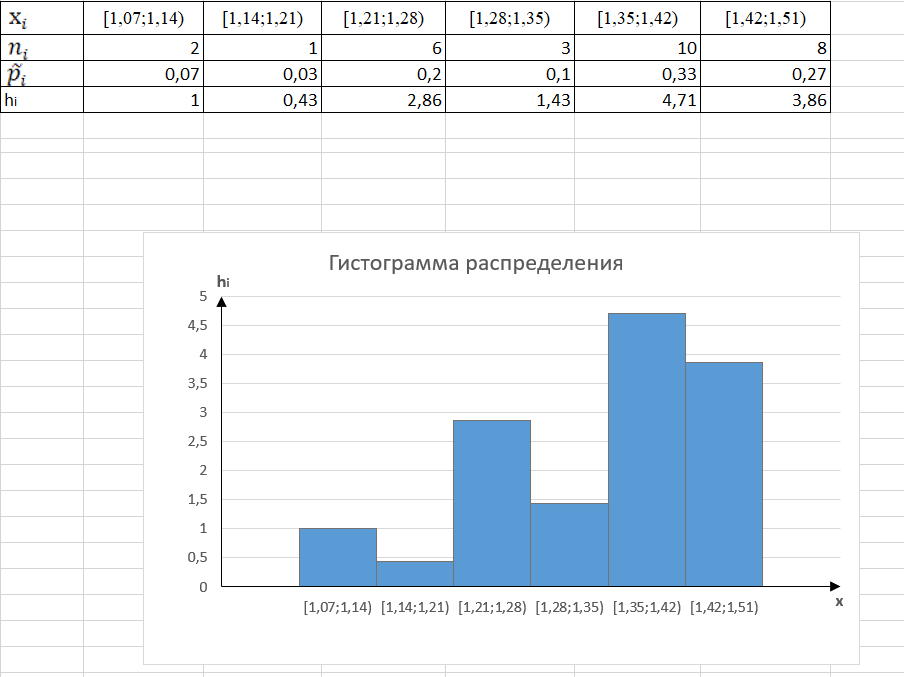
Выполним группировку данных:

Число интервалов m =

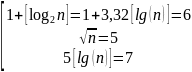
Величина интервала разбиения: h = 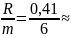0,07

Начало первого интервала: 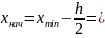1,07

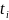– центр i-го интервала.

	[1,07;1,14)	[1,14;1,21)	[1,21;1,28)	[1,28;1,35)	[1,35;1,42)	[1,42;1,51)
	2	1	6	3	10	8
	0,07	0,03	0,2	0,1	0,33	0,27
	1	0,43	2,86	1,43	4,71	3,86
	1,11	1,18	1,25	1,32	1,39	1,47

Построим гистограмму распределения:

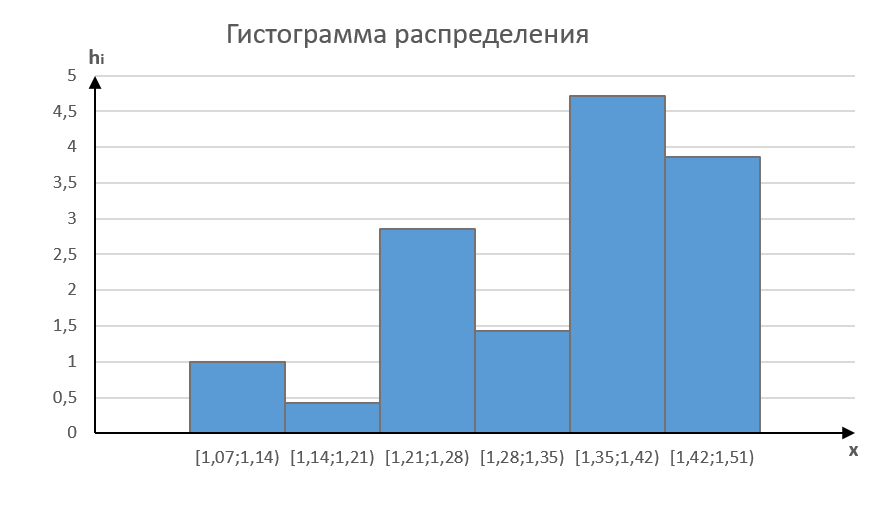
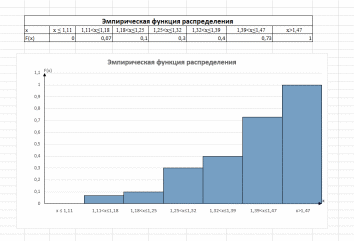
Эмпирическая функция распределения:

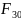(x) =

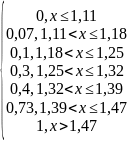
Построим график эмпирической функции распределения:

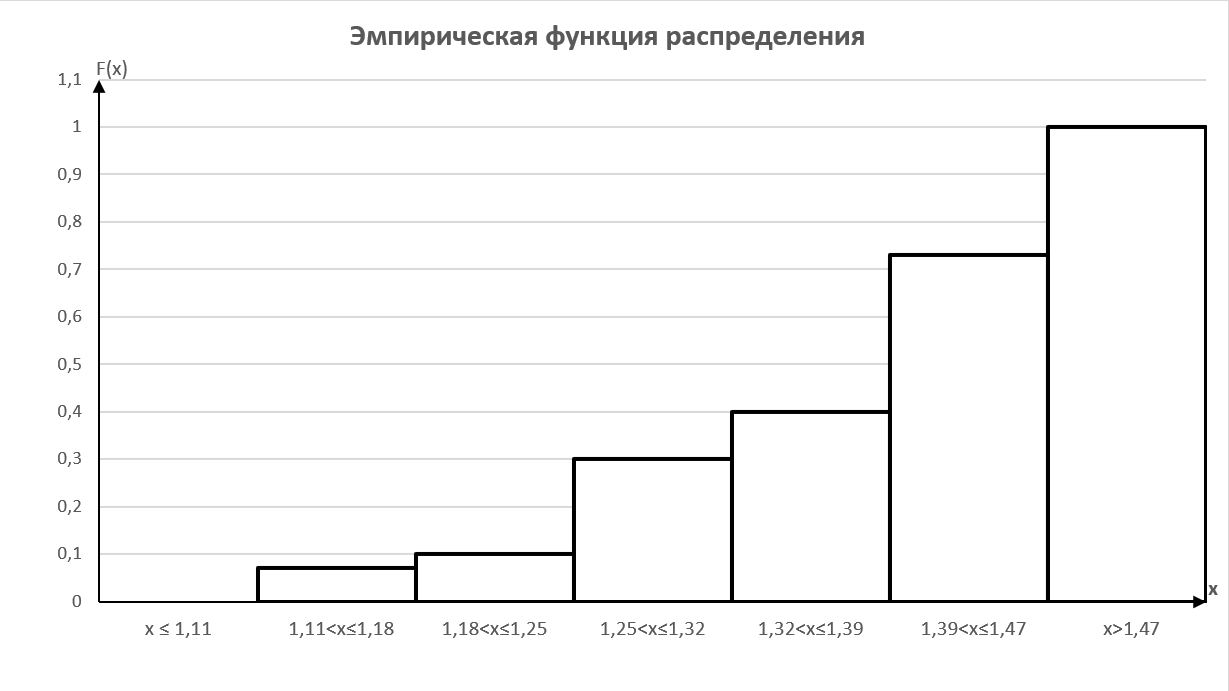
Вычислим основные описательные статистики.

Выборочное среднее:

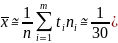
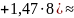1,35 Выборочная смещенная дисперсия:

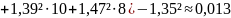
Выборочная несмещенная (исправленная) дисперсия:

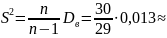0,0134

Среднеквадратическое отклонение:

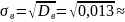0,114

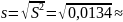0,116

Выборочная мода:

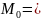[1,35;1,42)

Выборочная медиана:

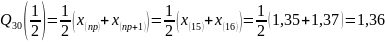
Нижняя квартиль:

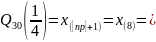1,27

Верхняя квартиль:

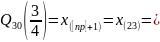1,42

Интерквартильный размах:

Iqr =

«Усы» для «ящика с усами»:

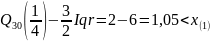
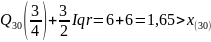
Построим «ящик с усами» (т.к. выбросов нет – строим по и ):

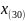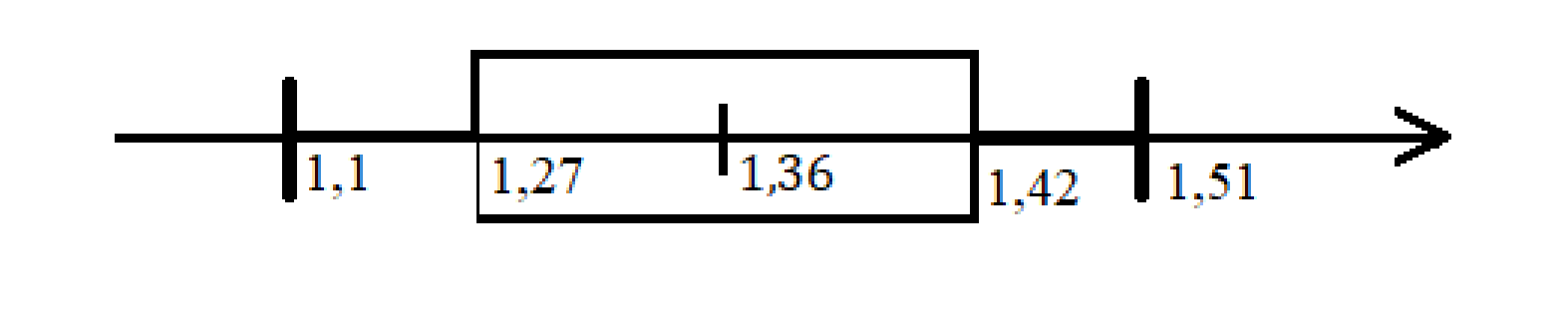
3. Результаты выполнения вычислений в Excel

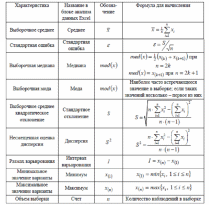
Задание 1.

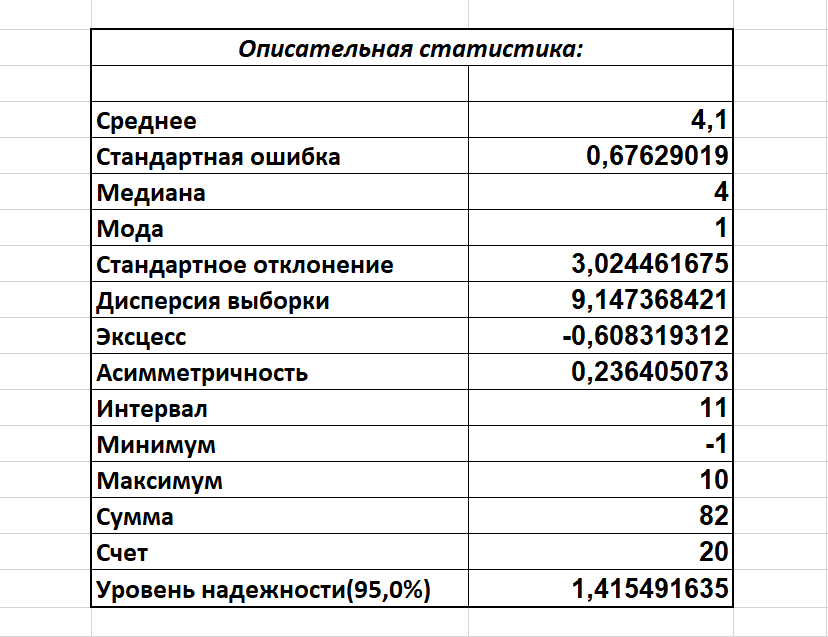
Задание 2.

4. Выводы

В данной работе я научился по представленным выборкам дискретной и непрерывной генеральных совокупностей строить вариационный ряд, находить интервал варьирования и размах, выполнять группировку данных, находить выборочное среднее, смещенную и несмещенную дисперсию, среднеквадратическое отклонение, моду, выборочную медиану, нижнюю и верхнюю квартиль. Строить полигон частот, гистограмму распределения, график эмпирической функции распределения и «ящик с усами».