
ВНИЗУ КОД НА C++
Лабораторная работа 4 (Вариант 15)
Метод ветвей и границ для решения задачи
Коммивояжера
Лаб. Раб. №2, Часть 2, задание 1, 3, 4
![]()
![]()
import heapq
import sys
N = 5 #количество узлов графа
INF = sys.maxsize #значение вместо бесконечности
#узлы
class Node:
def __init__(self, parentMatrix, path, level, i, j):
self.path = path.copy()
#пропуск корневого узла
if level != 0:
self.path.append((i, j)) #добавление к пути текущего ребра
#print(f"PATH: {self.path}")
#копирование данных из родительского узла в текущий узел
self.reducedMatrix = [row[:] for row in parentMatrix]
#print(f"selfMATRIX: {self.reducedMatrix}")
#print("\n")
#изменение значений на i-ой строке и j-ом столбце на бесконечность
for k in range(N):
if level != 0:
self.reducedMatrix[i][k] = INF
self.reducedMatrix[k][j] = INF
self.reducedMatrix[j][0] = INF
#self.cost = 0 #нижняя граница
self.vertex = j #номер текущего города
self.level = level #количество посещённых городов на данный момент
def __lt__(self, other):
return self.cost < other.cost
#приведение матрицы по строкам
def rowReduction(reducedMatrix, row):
for i in range(N):
row[i] = min(reducedMatrix[i])
for i in range(N):
for j in range(N):
if reducedMatrix[i][j] != INF and row[i] != INF:
reducedMatrix[i][j] -= row[i]
#приведение матрицы по столбцам
def columnReduction(reducedMatrix, col):
for i in range(N):
col[i] = min(reducedMatrix[j][i] for j in range(N))
for i in range(N):
for j in range(N):
if reducedMatrix[i][j] != INF and col[j] != INF:
reducedMatrix[i][j] -= col[j]
#получение нижней границы пути, начинающегося с ткущего минимального элемента
def calculateCost(reducedMatrix):
cost = 0
row = [0] * N #значение каждой строки, на которое она уменишилась
col = [0] * N #значение каждого столбца, на которое он уменишился
rowReduction(reducedMatrix, row)
columnReduction(reducedMatrix, col)
#print(f"redMATR: {reducedMatrix}")
for i in range(N):
cost += row[i] if row[i] != INF else 0
cost += col[i] if col[i] != INF else 0
#print(f"cost: {cost}")
return cost
#вывод пар вершин по которым проходит путь
def printPath(list_):
for i in range(len(list_)):
print(f"{list_[i][0] + 1} -> {list_[i][1] + 1}")
def solve(costMatrix):
priority_queue = [] #приоритетная очередь для хранения активных узлов дерева поиска
root = Node(costMatrix, [], 0, -1, 0) #создание корневого узла
root.cost = calculateCost(root.reducedMatrix) #получение нижней границы пути, начинающегося в узле 0
#print(f"ROOT.COST: {root.cost}\n")
heapq.heappush(priority_queue, root) #добавление корневого узла в список активных узлов
#print(f"PQ: {priority_queue[0].reducedMatrix}\n")
#нахождение активных узлов с наименьшей стоимостью, добавление потомков в список активыных узлов
while priority_queue:
#нахождение активного узла с наименьшей стоимостью и удаление его из списка активных узлов
min_ = heapq.heappop(priority_queue) #объект класса Node
#print(f"MR: {min_.reducedMatrix}\n")
i = min_.vertex #текущий номер города
#если все города посещены
if min_.level == N - 1:
min_.path.append((i, 0)) #возвращение в начальный город
printPath(min_.path) #вывод списка посещённых городов
return min_.cost #возврат минимальной стоимости пути
#определение гранчного значения для каждого потомка
for j in range(N):
if min_.reducedMatrix[i][j] != INF :
#создание потомка и вычисление его стоимости
#print(f"j: {i}, {j}")
#print(f"minMATRIX: {min_.reducedMatrix}")
#print(f"minPATH: {min_.path}")
#print(f"minLEVEL: {min_.level + 1}\n")
child = Node(min_.reducedMatrix, min_.path, min_.level + 1, i, j)
child.cost = min_.cost + min_.reducedMatrix[i][j] + calculateCost(child.reducedMatrix)
#print(f"minCOST: {min_.cost}")
#print(f"minIJ {min_.reducedMatrix[i][j]}")
#print(f"childCOST: {child.cost}\n")
heapq.heappush(priority_queue, child) #добавление потомка к активным узлам
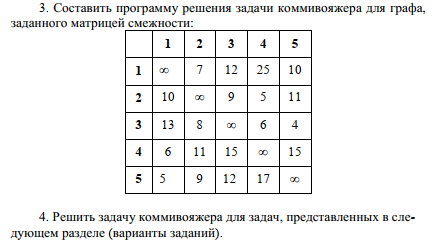
costMatrix1 = [
[INF, 7, 12, 25, 10],
[10, INF, 9, 5, 11],
[13, 8, INF, 6, 4],
[6, 11, 15, INF, 15],
[5, 9, 12, 17, INF]
]
costMatrix2 = [
[INF, 7, 12, 25, 10],
[10, INF, 9, INF, 11],
[13, 8, INF, 6, 4],
[6, 11, 15, INF, 15],
[5, 9, 12, 17, INF]
]
print(f"Стоимость пути: {solve(costMatrix1)}")
Машина Тьюринга Лаб. Раб. №5, Часть 2, задание 1
![]()
![]()
def convert(unary_input):
result = 0
if unary_input == "":
unary_input = "0"
else:
for i in range(len(unary_input)):
if unary_input[i] != '|':
raise ValueError("Введена не унарная запись")
result += 1
if result > 9:
#raise ValueError("Количесвто символов больше 9")
return unary_input[result - 2]
unary_input = unary_input[:i] + str(result) + unary_input[i+1:]
#print(unary_input)
return unary_input[result - 1]
unary_input = "||||"
result = convert(unary_input)
print(f"{unary_input}: {result}")
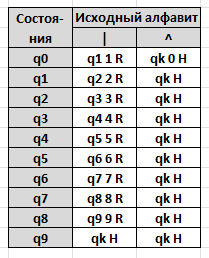
Функциональная таблица
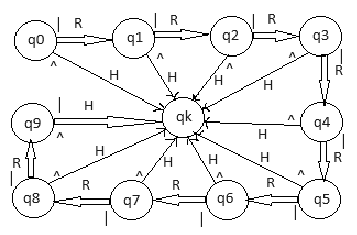
Функциональная диаграмма
Ответы на вопросы:
Лаб. Раб. №2:
Каковы основные принципы метода ветвей и границ?
1. Разбиение задачи на подзадачи: исходная задача разбивается на более мелкие подзадачи, которые могут быть решены отдельно.
2. Построение дерева поиска: создается дерево решений, в котором каждая ветвь представляет потенциальное решение, а каждый узел представляет частичное решение.
3. Оценка верхних и нижних границ: для каждого частичного решения вычисляются верхняя и нижняя границы, которые используются для определения того, стоит ли продолжать поиск в данной ветви.
4. Обрезание ветвей: если верхняя граница ветви ниже, чем текущее лучшее решение, ветвь обрезается, и поиск продолжается в других ветвях.
5. Поиск оптимального решения: Процесс разветвления и обрезания продолжается до тех пор, пока не будет найдено оптимальное решение или пока не будут исследованы все ветви.
Какое множество называется рекордом?
В математике множество называется рекордом, если оно содержит наибольший или наименьший элемент среди всех множеств, удовлетворяющих определенным условиям.
Как сформулировать условие задачи коммивояжера?
Дано множество из N городов, и для каждой пары городов известно расстояние между ними. Задача коммивояжера заключается в том, чтобы найти самый короткий путь, проходящий через каждый город ровно один раз и возвращающийся в исходный город.
Что означает привести матрицу по строкам?
Пусть имеется некоторая числовая матрица. Привести строку этой матрицы означает выделить в строке минимальный элемент (его называют константой приведения) и вычесть его из всех элементов этой строки.
Как строится дерево перебора для расшифровки криптограмм?
Для расшифровки криптограмм с помощью метода перебора строится дерево перебора, которое представляет собой дерево всех возможных комбинаций символов и их сочетаний, которые могут быть использованы для расшифровки криптограммы.
Процесс построения дерева перебора для расшифровки криптограмм обычно выглядит следующим образом:
1. Выбор алфавита: определение возможных символов, которые могут встречаться в расшифрованном тексте, например, буквы алфавита, цифры, знаки препинания и т. д.
2. Построение дерева: для каждой позиции в криптограмме создается уровень дерева, где каждая ветвь представляет возможные расшифровки для данной позиции. Например, если на первой позиции в криптограмме может стоять буква "A", "B" или "C", то на первом уровне дерева будет три ветви, соответствующие этим вариантам.
3. Расшифровка: далее происходит рекурсивный процесс, где для каждой ветви на текущем уровне дерева рассматриваются возможные варианты для следующей позиции, и так далее, пока не будет достигнут конец криптограммы или найдено правильное расшифрованное сообщение.
4. Оценка результатов: каждый найденный вариант расшифровки оценивается с помощью методов частотного анализа, статистики биграмм и триграмм, а также контекстуального анализа, чтобы определить, насколько вероятно, что данный вариант является правильным.
Что такое функция штрафа?
Функция штрафа – это множество чисел, вычисленных для каждого нуля приведенной матрицы посредством суммирования двух минимальных чисел, из той строки и того столбца, в которых расположен нулевой элемент.
Как исключается досрочное завершение тура?
Если скорректированная матрица имеет размер 2 × 2, и если узел дерева, которому соответствует эта матрица, имеет минимальную граничную оценку, то решение задачи заканчивается: два оставшихся нуля этой матрицы соответствуют двум последним ребрам, которые включаются в тур непосредственно, при этом, очевидно, стоимость тура не изменяется.
Что такое нижняя граничная оценка?
Минимальное значение, которое может принимать решение оптимизационной задачи при заданных условиях.
