ВНИЗУ КОД НА C++
Лабораторная работа 3 (Вариант 15) Алгоритмы нахождения кратчайших путей на графах Лаб. Раб. №5, Часть 1, задание 1
import sys
import time
class Edge:
def __init__(self, target, weight):
self.target = target
self.weight = weight
def findShortestPath(graph, start, end):
n = len(graph)
dist = [sys.maxsize] * n #создание массива для хранения длин путей
dist[start] = 0 #начальная вершина имеет расстояние 0
pred = [-1] * n #массив для хранения предшественников вершин в кратчайшем пути
for i in range(2):
#print(f"\n{i}:")
for u in range(n):
#print(f"{u}:")
for e in graph[u]:
v, weight = e.target, e.weight
#print(f"{v}: {weight}")
if dist[u] != sys.maxsize and dist[u] + weight < dist[v]:
dist[v] = dist[u] + weight
pred[v] = u
#print(f"YES: {dist[v]}")
for i in range(n):
print(f"f{i + 1}: {dist[i]}")
print("Путь:", end=" ")
path = []
current = end
while current != -1:
path.append(current)
current = pred[current]
print(" -> ".join(str(i + 1) for i in reversed(path)))
return dist[end] #возврат длины кратчайшего пути до конечной вершины
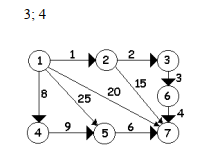
graph1 = [
[Edge(1, 1), Edge(6, 20), Edge(4, 25), Edge(3, 8)],
[Edge(2, 2), Edge(6, 15)],
[Edge(5, 3)],
[Edge(4, 9)],
[Edge(6, 6)],
[Edge(6, 4)],
[]
]
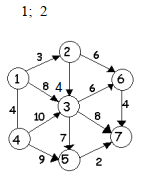
graph2 = [
[Edge(1, 3), Edge(2, 8), Edge(3, 4)],
[Edge(5, 6), Edge(2, 4)],
[Edge(5, 6), Edge(6, 8), Edge(4, 7)],
[Edge(2, 10), Edge(4, 9)],
[Edge(6, 2)],
[Edge(6, 4)],
[]
]
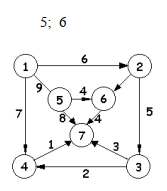
graph3 = [
[Edge(1, 6), Edge(4, 9), Edge(3, 7)],
[Edge(5, 2), Edge(2, 5)],
[Edge(3, 2), Edge(6, 3)],
[Edge(6, 1)],
[Edge(5, 4), Edge(6, 8)],
[Edge(6, 4)],
[]
]
start, end = 1, 7
start -= 1
end -= 1
start_time = time.time()
shortest_path = findShortestPath(graph1, start, end)
end_time = time.time()
if shortest_path == sys.maxsize:
print("Пути между вершинами не существует")
else:
print(f"Кратчайший путь от вершины {start + 1} до вершины {end + 1} равен {shortest_path}")
print(f"Время решения задачи: {end_time - start_time} секунд")
Ответы на вопросы:
Лаб. Раб. №5:
Какова теоретическая сложность алгоритмов, рассмотренных в настоящей лабораторной работе?
1. В общем случае, временная сложность метода динамического программирования может быть выражена как O(n*m), где n - размерность задачи, а m - размерность подзадачи.
2. Метод Дейкстры: Временная сложность алгоритма Дейкстры для нахождения кратчайшего пути в графе с неотрицательными весами ребер составляет O((V + E) * log V), где V - количество вершин, а E - количество ребер в графе.
3. Алгоритм Флойда: Временная сложность алгоритма Флойда для нахождения всех кратчайших путей взвешенного ориентированного графа составляет O(V^3), где V - количество вершин в графе.
4. Алгоритм Йена: Временная сложность алгоритма Йена для нахождения K кратчайших путей в графе зависит от реализации, но обычно она составляет O(K * (V^2 + E * log V)), где V - количество вершин, E - количество ребер, а K - количество кратчайших путей.
5. Алгоритм Беллмана-Форда: Временная сложность алгоритма Беллмана-Форда для нахождения кратчайших путей в графе с отрицательными весами ребер составляет O(V * E), где V - количество вершин, а E - количество ребер в графе.