Лабораторная работа 2 (Вариант 15) Итеративные и рекурсивные алгоритмы, Алгоритмы построения остовного (покрывающего) дерева сети Лаб. Раб. №3, Часть 1, задание 3
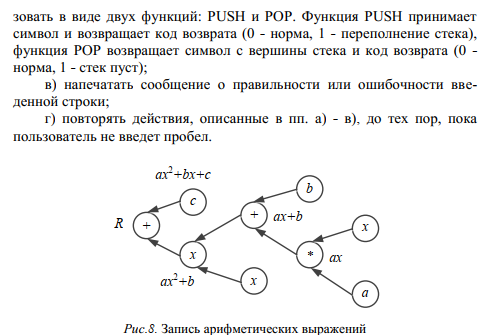
#include <iostream>
#include <stack>
#include <string>
using namespace std;
const int MAX_STACK_SIZE = 1000;
// if (bracketsStack.size() >= bracketsStack.max_size())
// Функция для добавления элемента в стек (PUSH)
int push(stack<char>& bracketsStack, char bracket) {
if (bracketsStack.size() >= MAX_STACK_SIZE) {
return 1; // Переполнение стека
}
bracketsStack.push(bracket);
return 0; // Норма
}
// Функция для извлечения элемента из стека (POP)
pair<char, int> pop(stack<char>& bracketsStack) {
if (bracketsStack.empty()) {
return make_pair('\0', 1); // Стек пуст
}
char bracket = bracketsStack.top();
bracketsStack.pop();
return make_pair(bracket, 0); // Норма
}
// Функция для проверки правильности расстановки скобок
bool checkBrackets(const string& expression) {
stack<char> bracketsStack;
for (char bracket : expression) {
if (bracket == '(') {
push(bracketsStack, bracket);
} else if(bracket == ')') {
auto result = pop(bracketsStack);
if (result.second == 1) {
return false; // Стек пуст
}
}
}
return bracketsStack.empty();
}
int main() {
string input;
do {
cout << "Введите арифметическое выражение: ";
getline(cin, input);
if (input.find('(') == string::npos && input.find(')') == string::npos) {
cout << "Введенное выражение не содержит скобок." << endl;
} else {
if (checkBrackets(input)) {
cout << "Скобки расставлены верно." << endl;
} else {
cout << "Ошибка в расстановке скобок." << endl;
}
}
} while (input != " ");
return 0;
}
Лаб. Раб. №3, Часть 1, задание 4
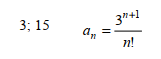
#include <iostream>
#include <stack>
using namespace std;
double calculateExpression(int n, stack<double>& stack) {
if (n == 0) {
stack.push(3.0);
return 3.0; // Базовый случай: a_0 = 3^1 / 0! = 3
}
double result = 3 * calculateExpression(n - 1, stack) / n;
stack.push(result);
return result;
}
int main() {
int n;
do {
cout << "Введите значение n для вычисления a_n (неотрицательное): ";
cin >> n;
} while (n < 0);
stack<double> stack;
double result = calculateExpression(n, stack);
cout << "a_" << n << " = " << result << endl;
while (!stack.empty()) {
cout << "Шаг " << n << ": " << stack.top() << endl;
stack.pop();
n--;
}
return 0;
}
Лаб. Раб. №4, Часть 1, задание 5
Метод Крускала:
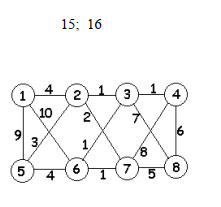
Метод Прима:
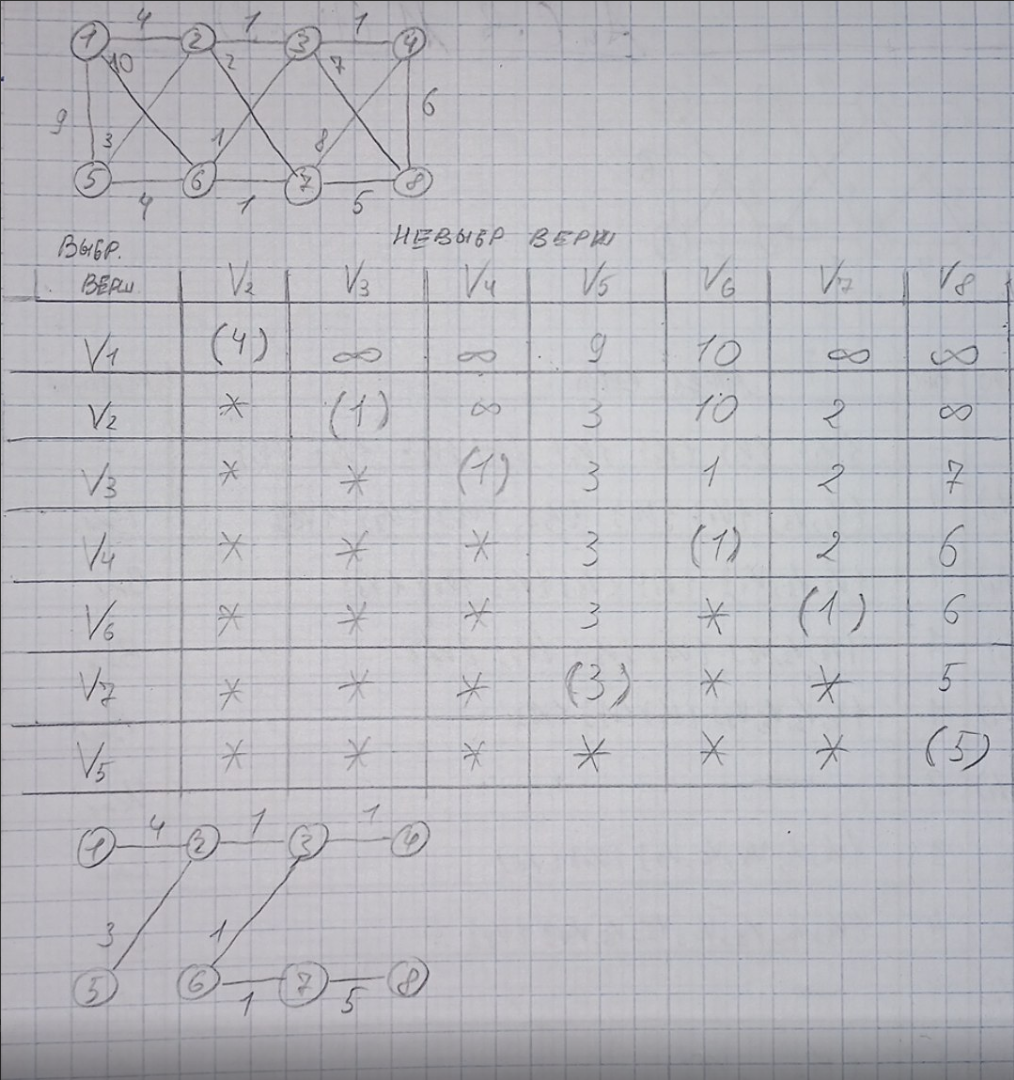
Лаб. Раб. №4, Часть 1, задание 6
Метод Крускала:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
// Структура для представления ребра графа
struct Edge {
int src, dest, weight;
};
// Структура для представления набора подмножеств для алгоритма Крускала
struct Subset {
int parent, rank;
};
// Функция для поиска корня подмножества
int find(std::vector<Subset>& subsets, int i) {
cout << "Пришло: " << i << endl;
if (subsets[i].parent != i) {
subsets[i].parent = find(subsets, subsets[i].parent);
}
cout << "Вышло: " << subsets[i].parent << endl;
return subsets[i].parent;
}
// Функция для объединения двух подмножеств в одно
void Union(std::vector<Subset>& subsets, int x, int y) {
int xroot = find(subsets, x);
cout << "xroot: " << x << endl;
int yroot = find(subsets, y);
cout << "yroot: " << y << endl;
if (subsets[xroot].rank < subsets[yroot].rank) {
subsets[xroot].parent = yroot;
} else if (subsets[xroot].rank > subsets[yroot].rank) {
subsets[yroot].parent = xroot;
} else {
subsets[yroot].parent = xroot;
subsets[xroot].rank++;
}
}
// Функция для построения остовного дерева методом Крускала
void KruskalMST(std::vector<Edge>& edges, int V) {
std::vector<Edge> result; // Результат - остовное дерево
std::sort(edges.begin(), edges.end(), [](const Edge& a, const Edge& b) {
return a.weight < b.weight;
}); // Сортировка по возрастанию весов рёбер
std::vector<Subset> subsets(V);
for (int i = 0; i < V; i++) {
subsets[i] = {i, 0};
}
cout << endl << "S: " << endl;
for (int i = 0; i < V; i++) {
cout << "p:" << subsets[i].parent << " r: " << subsets[i].rank << endl;
}
int e = 0; // Индекс результата
int i = 0; // Индекс ребер
while (e < V - 1 && i < edges.size()) {
Edge next_edge = edges[i++];
cout << endl << "i: " << i << endl;
int x = find(subsets, next_edge.src);
cout << "x: " << x << endl;
int y = find(subsets, next_edge.dest);
cout << "y: " << y << endl;
if (x != y) {
result.push_back(next_edge);
Union(subsets, x, y);
cout << endl << "S: " << endl;
for (int i = 0; i < V; i++) {
cout << "p:" << subsets[i].parent << " r: " << subsets[i].rank << endl;
}
e++;
}
}
// Вывод остовного дерева
std::cout << "Остовное дерево по методу Крускала:" << std::endl;
for (const Edge& edge : result) {
std::cout << edge.src << " - " << edge.dest << " : " << edge.weight << std::endl;
}
}
int main() {
// Количество вершин
int V = 8;
std::vector<Edge> edges = {{1, 2, 4}, {1, 5, 9}, {1, 6, 10}, {2, 5, 3},
{2, 3, 1}, {2, 7, 2}, {3, 6, 1}, {3, 4, 1},
{3, 8, 7}, {4, 7, 8}, {4, 8, 6}, {5, 6, 4},
{6, 7, 1}, {7, 8, 5}};
KruskalMST(edges, V);
return 0;
}