Фибоначчиев поиск

В этом поиске анализируются элементы, находящиеся в позициях,

равных числам Фибоначчи. Числа Фибоначчи получаются по следующему правилу: каждое последующее число равно сумме двух предыдущих чисел.

Интерполяционный поиск

Исходное множество должно быть упорядоченно по возрастанию

весов. Первоначальное сравнение осуществляется на расстоянии шага

d, который определяется по формуле:

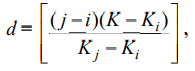
где j - номер последнего рассматриваемого элемента; i - номер первого

рассматриваемого элемента; K - отыскиваемый ключ;

Ki, K j – значения ключей в i-й и j-й позициях; [ ] - целая часть числа.

Идея метода заключается в следующем: шаг d меняется после каждого этапа по формуле, приведенной выше. Алгоритм заканчивает работу при d = 0. В этом случае осуществляется анализ соседних элементов,

после чего делается окончательный вывод о результатах поиска (рис.2).

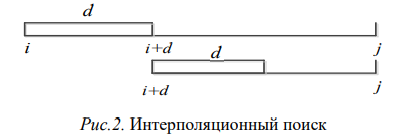
Этот метод прекрасно работает, если исходное множество представляет собой арифметическую прогрессию или множество, приближенное к ней.

Поиск по бинарному дереву

Использование структуры бинарного дерева позволяет быстро

вставлять и удалять записи и проводить эффективный поиск по таблице.

Такая гибкость достигается добавлением в каждую запись двух полей

для хранения ссылок.

Методы поиска, основанные на числовых свойствах ключей Поиск по бору

Особую группу методов поиска образует представление ключей в

виде последовательности цифр и букв. Рассмотрим, например, имеющиеся во многих словарях буквенные высечки (гнезда). Тогда по первой

букве данного слова можно отыскать страницы, содержащие все слова,

начинающиеся с этой буквы. Развивая идею побуквенных высечек, получим схему поиска, основанную на индексации в структуре бора (термин использует часть слова «выборка»).

Бор имеет вид m-арного дерева. Каждый узел уровня h представляет множество всех ключей, начинающихся с определенной последовательности из h литер. Узел определяет m-путевое разветвление в зависимости от (h + 1)-й литеры.

Поиск хешированием

В основе поиска лежит переход от исходного множества к множеству хеш-функций h(k). Хеш-функция, основанная на делении, имеет

следующий вид:

h(k) = k mod (m), где k - ключ; mod - целочисленный остаток от деления; m - целое число.

Алгоритмы поиска словесной информации

В настоящее время наличие сверхпроизводительных микропроцессоров и дешевизна электронных компонентов позволяют делать значительные успехи в алгоритмическом моделировании. Рассмотрим

несколько алгоритмов обработки слов.

Алгоритм Кнута - Морриса - Пратта (кмп)

Данный алгоритм получает на вход слово

X = x[1]x[2]... x[n]

и просматривает его слева направо буква за буквой, заполняя при этом

массив натуральных чисел l[1]... l[n], где l[i] - длина слова l(x[1]... х[i]).

Таким образом, l[i] есть длина наибольшего начала слова x[1]... x[i],

одновременно являющегося его концом.

Алгоритм Бойера - Мура (БМ)

Этот алгоритм читает лишь небольшую часть всех букв слова, в

котором ищется заданный образец.

Пусть, например, отыскивается образец abcd. Посмотрим на четвертую букву слова: если это буква e, то нет необходимости читать первые три буквы. (В самом деле, в образце буквы e нет, поэтому он может

начаться не раньше пятой буквы.)

Рассмотрим простой вариант этого алгоритма, который не гарантирует быстрой работы во всех случаях. Пусть x[1]... х[n] - образец, который надо отыскать. Для каждого символа s найдем самое правое его

вхождение в слово X, т.е. наибольшее k, при котором х[k] = s. Эти сведения будем хранить в массиве pos[s]; если символ s вовсе не встречается, то можно предположить, что pos[s] = 0.