Лабораторная работа 1 (Вариант 15) Методы сортировки, Методы поиска
Лаб. Раб. №1, Часть 1, задание 3, задание 8 + Лаб. Раб. №2, Часть 1, задание 6
#include <iostream>
#include <ctime>
using namespace std;
void SimpleInsertion(int arr[], int n) {
for (int i = 1; i < n; i++) {
int key = arr[i];
int j = i - 1;
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key;
}
}
void HoareSorting(int arr[], int low, int high) {
if (low < high) {
int pivot = arr[low];
int i = low;
int j = high;
while (i <= j) {
while (arr[i] < pivot) i++;
while (arr[j] > pivot) j--;
if (i <= j) {
swap(arr[i], arr[j]);
i++;
j--;
}
}
HoareSorting(arr, low, j);
HoareSorting(arr, i, high);
}
}
int interpolationSearch(int arr[], int size, int x) {
int low = 0;
int high = size - 1;
while (low <= high && x >= arr[low] && x <= arr[high]) {
int pos = low + ((high - low) * (x - arr[low])/ (arr[high] - arr[low]));
if (arr[pos] == x) {
return pos + 1;
}
if (arr[pos] < x) {
low = pos + 1;
} else {
high = pos - 1;
}
}
return -1;
}
int main() {
const int size = 1000;
int arr[size];
srand(time(0));
for (int i = 0; i < size; i++) {
arr[i] = rand() % size; // случайные числа от 0 до 999
}
cout << "Массив до сортировки:" << endl;
for (int i = 0; i < size; i++) {
cout << arr[i] << " ";
}
cout << endl << endl;
clock_t start = clock();
// SimpleInsertion(arr, size);
HoareSorting(arr, 0, size - 1);
clock_t end = clock();
cout << "Массив после сортировки:" << endl;
for (int i = 0; i < size; i++) {
cout << arr[i] << " ";
}
cout << endl;
double timeSort = double(end - start) / CLOCKS_PER_SEC;
cout << "Время сортировки: " << timeSort << " секунд" << endl << endl;
int elementToFind = rand() % size;
clock_t startSearch = clock();
int pos = interpolationSearch(arr, size, elementToFind);
clock_t endSearch = clock();
if (pos != -1) {
cout << "Элемент " << elementToFind << " найден на позиции " << pos << endl;
} else {
cout << "Элемент " << elementToFind << " не найден" << endl;
}
double timeSearch = double(endSearch - startSearch) / CLOCKS_PER_SEC;
cout << "Время, затраченное на поиск: " << timeSearch << " секунд" << endl;
return 0;
}
Конспект:
Лабораторная работа № 1
Методы сортировки
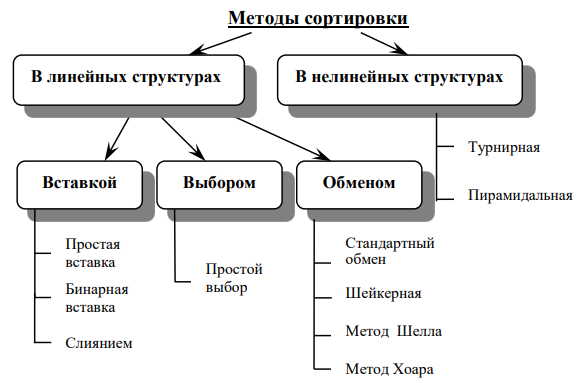
Сортировка в линейных структурах
Сортировка выбором
Сортировка выбором состоит в том, что сначала в неупорядоченном списке выбирается и отделяется от остальных наименьший элемент.
После этого исходный список оказывается измененным. Измененный
список принимается за исходный и процесс продолжается до тех пор,
пока все элементы не будут выбраны. Очевидно, что выбранные
элементы образуют упорядоченный список.
Сортировка вставкой
Метод сортировки вставкой предусматривает поочередный выбор
из неупорядоченной последовательности элементов каждого элемента,
сравнение его с предыдущим, уже упорядоченным, и перемещение на
соответствующее место.
Сортировка бинарной вставкой
При использовании метода сортировки вставками ключ i-го
элемента сравнивается приблизительно с i/2 ключами уже отсортированных элементов. Для того чтобы ускорить этот процесс, Джон Мочлив предложил использовать метод бинарных вставок, т.е. сравнивать
ключ i-го элемента (Ki) с ключом середины уже отсортированной последовательности (Ki/2). Затем в зависимости от того, ключ Ki меньше
или больше Ki/2, будем рассматривать следующие элементы:
[K1; Ki/2–1] или [Ki/2 + 1; Ki].
Для решения проблемы нечетного числа элементов множества номер центрального элемента вычисляется по формуле:
mid: = (low + high) div 2.
Поскольку процесс сравнения занимает относительно малый промежуток времени, а перемещать придется для i-го элемента в среднем
i/2 элементов, время, необходимое на реализацию алгоритма, все равно
пропорционально 1/4·n^2. Сложность метода сортировки бинарной
вставкой такая же, как и у метода простой вставки.
Сортировка обменом
В сортировке обменом элементы списка последовательно сравниваются между собой и меняются местами в том случае, если предшествующий элемент больше последующего. Требуется, например, провести сортировку списка методом стандартного обмена, или методом
«пузырька».