ЛР10

import numpy as np import sympy as sp from numpy import * from sympy import * import matplotlib.pyplot as plt

Пример 1

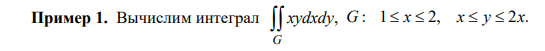
import sympy as sp from sympy.abc import x, y f = x * y c, d = (x, 2*x) a, b = (1, 2) Iy = sp.integrate(f, (y, c, d)) Ix = sp.integrate(Iy, (x, a, b)) print(f'I = {Ix}')

I = 45/8

Упражнение 1

def field(f, g, a, b, n, x1, x2, y1, y2): dx=(b-a)/n fy=[0]*(n+1) gy=[0]*(n+1) k=0 rx=[0]*(n+1) for i in arange(a, b+dx, dx): fy[k]=f.subs(x,i) gy[k]=g.subs(x,i) rx[k]=i k+=1 for i in range(1,n+1): plt.plot([rx[i-1],rx[i]],[fy[i-1],fy[i]],'-',color='indigo') plt.plot([rx[i-1],rx[i]],[gy[i-1],gy[i]],'-',color='teal') k=0 for i in arange(a, b+dx, dx): plt.plot([i,i],[fy[k],gy[k]],'-',color='coral') k+=1 plt.xlim([x1,x2]) plt.ylim([y1,y2]) plt.grid() plt.show() x=Symbol('x') f=2*x g=x**2 a=0 b=2 n=50 x1=-2 x2=4 y1=-2 y2=6 field(f, g, a, b, n, x1, x2, y1, y2)

from sympy.abc import x, y f = x+y**2 c, d = (x**2, 2*x) a, b = (0, 2) Iy = sp.integrate(f, (y, c, d)) Ix = sp.integrate(Iy, (x, a, b)) print(f'I = {Ix}')

I = 124/21

from sympy.abc import x, y f = x+y**2 c, d = (y/2, sqrt(y)) a, b = (0, 4) Iy = sp.integrate(f, (x, c, d)) Ix = sp.integrate(Iy, (y, a, b)) print(f'I = {Ix}')

I = 124/21

Упражнение 2

import matplotlib.pyplot as plt import numpy as np from matplotlib import cm fig = plt.figure() ax = fig.add_subplot(projection = '3d') xs = np.linspace(0, 1, 50) ys = np.linspace(0, 1, 50) X, Y = np.meshgrid(xs, ys) Z = 1-X-Y ax.plot_surface(X, Y, Z, cmap=cm.cool, linewidth=0) xs = np.linspace(0, 1, 50) ys = np.linspace(0, 1, 50) X, Y = np.meshgrid(xs, ys) Z=X-X+Y-Y ax.plot_wireframe(X, Y, Z, rstride = 2, cstride = 2) xs = np.linspace(0, 1, 50) zs = np.linspace(0, 1, 50) X, Z = np.meshgrid(xs, zs) Y=X-X+Z-Z ax.plot_wireframe(X, Y, Z, rstride = 2, cstride = 2) ys = np.linspace(0, 1, 50) zs = np.linspace(0, 1, 50) Y, Z = np.meshgrid(ys, zs) X=Y-Y+Z-Z ax.plot_wireframe(X, Y, Z, rstride = 2, cstride = 2)

<mpl_toolkits.mplot3d.art3d.Line3DCollection at 0x6b82c38>

from sympy.abc import x, y, z ff = z e, f = (0, 1-x-y) c, d = (0, 1-x) a, b = (0, 1) Iz = sp.integrate(ff, (z, e, f)) Iy = sp.integrate(Iz, (y, c, d)) Ix = sp.integrate(Iy, (x, a, b)) print(f'I = {Ix}')

I = 1/24

Упражнение 3

x=Symbol('x') f=x-x g=sin(x) a=0 b=pi/2 n=50 x1=-1 x2=2 y1=-1 y2=2 field(f, g, a, b, n, x1, x2, y1, y2)

from sympy.abc import x, y f = cos(x)*sqrt(2-2*y) c, d = (0, sin(x)) a, b = (0, pi/2) Iy = sp.integrate(f, (y, c, d)) Ix = sp.integrate(Iy, (x, a, b)) print(f'I = {Ix}')

from sympy.abc import x, y f = cos(x)*sqrt(2-2*y) c, d = (asin(y), pi/2) a, b = (0, 1) Iy = sp.integrate(f, (x, c, d)) Ix = sp.integrate(Iy, (y, a, b)) print(f'I = {Ix}')

I = 2*sqrt(2)/5

Упражнение с1

x=Symbol('x') f=-x g=1-2*x**2 a=-0.5 b=1 n=50 x1=-1 x2=2 y1=-2 y2=2 field(f, g, a, b, n, x1, x2, y1, y2)

from sympy.abc import x, y f = sp.sin(x*y) c, d = (-x, 1-2*x**2) a, b = (-0.5, 1) Iy = sp.integrate(f, (y, c, d)) Ix = sp.integrate(Iy, (x, a, b)) print(f'I = {Ix}')

I = Integral(-cos(x**2)/x, (x, -0.5)) - Integral(-cos(x**2)/x, (x, 1)) + Integral(cos(2*x**3 - x)/x, (x, -0.5)) - Integral(cos(2*x**3 - x)/x, (x, 1))

from sympy.abc import x, y ff = sin(x*y) g, h = (-sqrt(0.5-0.5*y), sqrt(0.5-0.5*y)) e, f = (0.5, 1) c, d = (-y, sqrt(0.5-0.5*y)) a, b = (-1, 0.5) Iy = sp.integrate(ff, (x, c, d)) Ix = sp.integrate(Iy, (y, a, b)) Iy1 = sp.integrate(ff, (x, g, h)) Ix1 = sp.integrate(Iy1, (y, e, f)) II=Ix+Ix1 print(f'I = {II}')

I = Integral(-cos(y**2)/y, (y, -1)) - Integral(-cos(y**2)/y, (y, 0.5)) + Integral(cos(0.707106781186548*y*sqrt(1 - y))/y, (y, -1)) - Integral(cos(0.707106781186548*y*sqrt(1 - y))/y, (y, 0.5))