ЛР9

import numpy as np import sympy as sp from numpy import * from sympy import * import matplotlib.pyplot as plt

Упражнение 1

import matplotlib.pyplot as plt import numpy as np fig = plt.figure() xs = np.linspace(-4, 4, 50) ys = np.linspace(-4, 4, 50) X, Y = np.meshgrid(xs, ys) Z = X**3/3+Y**3/3 sx = np.linspace(-4, 5, 50) sz = np.linspace(-65, 85, 50) XX, ZZ = np.meshgrid(sx, sz) YY = (1-XX)/4 import matplotlib.pyplot as plt from matplotlib import cm import numpy as np fig, ax = plt.subplots(subplot_kw={"projection": "3d"}) # построение поверхности surf = ax.plot_surface(X, Y, Z, cmap=cm.cool, linewidth=0) surf1 = ax.plot_surface(XX, YY, ZZ, cmap=cm.winter, linewidth=0) # цветовой индикатор fig.colorbar(surf, shrink=0.5, aspect=5) fig.colorbar(surf1, shrink=0.5, aspect=5) plt.show()

<Figure size 640x480 with 0 Axes>

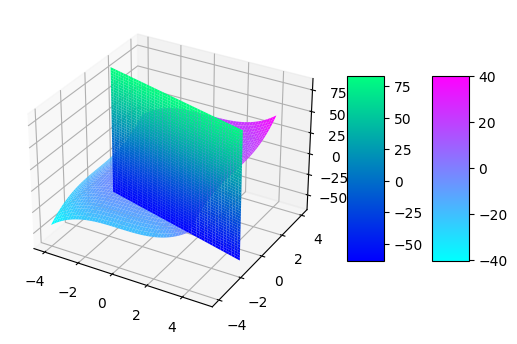
import matplotlib.pyplot as plt import numpy as np fig = plt.figure() xs = np.linspace(-4, 4, 50) ys = np.linspace(-4, 4, 50) X, Y = np.meshgrid(xs, ys) Z = (X+1)**2+Y**2 sx = np.linspace(0, 5, 50) sz = np.linspace(-5, 25, 50) XX, ZZ = np.meshgrid(sx, sz) YY = XX**(3/2) #ZZ = (XX+1)**2+YY**2 import matplotlib.pyplot as plt from matplotlib import cm import numpy as np fig, ax = plt.subplots(subplot_kw={"projection": "3d"}) # построение поверхности surf = ax.plot_surface(X, Y, Z, cmap=cm.cool, linewidth=0) surf1 = ax.plot_surface(XX, YY, ZZ, cmap=cm.winter, linewidth=0) surf2 = ax.plot_surface(XX, -YY, ZZ, cmap=cm.winter, linewidth=0) # цветовой индикатор fig.colorbar(surf, shrink=0.5, aspect=5) fig.colorbar(surf1, shrink=0.5, aspect=5) plt.show()

<Figure size 640x480 with 0 Axes>

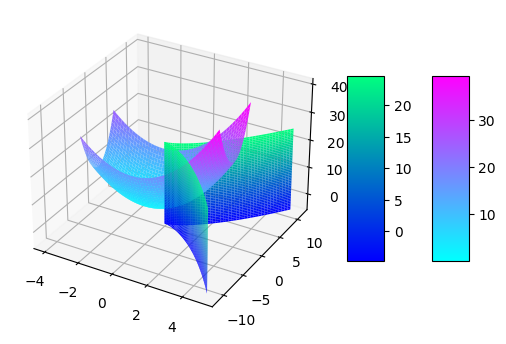
Упражнение 2

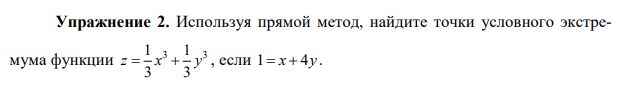
x, y = symbols('x y') z=x**3/3+y**3/3 xx=1-4*y zz=z.subs(x, xx) dz=diff(zz,y) yy=solve(dz) x_x=[0]*size(yy) z_z=[0]*size(yy) x_x[0]=xx.subs(y,yy[0]) x_x[1]=xx.subs(y,yy[1]) z_z[0]=zz.subs(y,yy[0]) z_z[1]=zz.subs(y,yy[1]) e1=[x_x[0], yy[0], z_z[0]] e2=[x_x[1], yy[1], z_z[1]] print(e1) print(e2)

[1/9, 2/9, 1/243] [-1/7, 2/7, 1/147]

Упражнение 3

Упражнение 4

def lagrang(z, xx): x, y, l = symbols('x y l') L=z+l*xx dx=diff(L,x) dy=diff(L,y) dl=diff(L,l) s=solve([dx,dy,dl]) print(s) ss=size(s) for i in range(0,ss): fdx=diff(xx,x) fdx=fdx.subs(x,s[i][x]) fdx=fdx.subs(y,s[i][y]) fdy=diff(xx,y) fdy=fdy.subs(x,s[i][x]) fdy=fdy.subs(y,s[i][y]) dx2=diff(dx,x) dx2=dx2.subs(x,s[i][x]) dx2=dx2.subs(y,s[i][y]) dx2=dx2.subs(l,s[i][l]) dy2=diff(dy,y) dy2=dy2.subs(x,s[i][x]) dy2=dy2.subs(y,s[i][y]) dy2=dy2.subs(l,s[i][l]) dxy=diff(dx,y) dxy=dxy.subs(x,s[i][x]) dxy=dxy.subs(y,s[i][y]) dxy=dxy.subs(l,s[i][l]) d=Matrix([[0,fdx,fdy],[fdx,dx2,dxy],[fdy,dxy,dy2]]) od=-det(d) if (od>0): print(i+1,': Условный минимум') if (od<0): print(i+1,': Условный максимум') if (od==0): print(i+1,': -?-') x, y = symbols('x y') z=z=x**3/3+y**3/3 xx=x+4*y-1 lagrang(z,xx)

[{l: -1/49, x: -1/7, y: 2/7}, {l: -1/81, x: 1/9, y: 2/9}] 1 : Условный максимум 2 : Условный минимум

x, y = symbols('x y') z=(x+1)**2+y**2 xx=y**2-x**3 lagrang(z,xx)

[{l: -1, x: -1/3 - sqrt(5)*I/3, y: -2**(3/4)*3**(1/4)*cos(atan(sqrt(5)/7)/2)/3 - 2**(3/4)*3**(1/4)*I*sin(atan(sqrt(5)/7)/2)/3}, {l: -1, x: -1/3 - sqrt(5)*I/3, y: 2**(3/4)*3**(1/4)*cos(atan(sqrt(5)/7)/2)/3 + 2**(3/4)*3**(1/4)*I*sin(atan(sqrt(5)/7)/2)/3}, {l: -1, x: -1/3 + sqrt(5)*I/3, y: -2**(3/4)*3**(1/4)*cos(atan(sqrt(5)/7)/2)/3 + 2**(3/4)*3**(1/4)*I*sin(atan(sqrt(5)/7)/2)/3}, {l: -1, x: -1/3 + sqrt(5)*I/3, y: 2**(3/4)*3**(1/4)*cos(atan(sqrt(5)/7)/2)/3 - 2**(3/4)*3**(1/4)*I*sin(atan(sqrt(5)/7)/2)/3}]

--------------------------------------------------------------------------- TypeError Traceback (most recent call last) Cell In[27], line 4 2 z=(x+1)**2+y**2 3 xx=y**2-x**3 ----> 4 lagrang(z,xx) Cell In[26], line 36, in lagrang(z, xx) 34 d=Matrix([[0,fdx,fdy],[fdx,dx2,dxy],[fdy,dxy,dy2]]) 35 od=-det(d) ---> 36 if (od>0): 37 print(i+1,': Условный минимум') 38 if (od<0): File /lib/python3.11/site-packages/sympy/core/relational.py:511, in Relational.__bool__(self) 510 def __bool__(self): --> 511 raise TypeError("cannot determine truth value of Relational") TypeError: cannot determine truth value of Relational

Упражнение 5

import matplotlib.pyplot as plt import numpy as np fig = plt.figure() xs = np.linspace(-4, 4, 50) ys = np.linspace(-4, 4, 50) X, Y = np.meshgrid(xs, ys) Z = X**2-2*X*Y-4*Y**2 sx = np.linspace(-5, 5, 100) sz = np.linspace(-65, 25, 100) XX, ZZ = np.meshgrid(sx, sz) YY = ((-25+2*XX**2)/4)**(1/2) #ZZ = (XX+1)**2+YY**2 import matplotlib.pyplot as plt from matplotlib import cm import numpy as np fig, ax = plt.subplots(subplot_kw={"projection": "3d"}) # построение поверхности surf = ax.plot_surface(X, Y, Z, cmap=cm.cool, linewidth=0) surf1 = ax.plot_surface(XX, YY, ZZ, cmap=cm.winter, linewidth=0) surf2 = ax.plot_surface(XX, -YY, ZZ, cmap=cm.winter, linewidth=0) # цветовой индикатор fig.colorbar(surf, shrink=0.5, aspect=5) fig.colorbar(surf1, shrink=0.5, aspect=5) plt.show()

<Figure size 640x480 with 0 Axes>

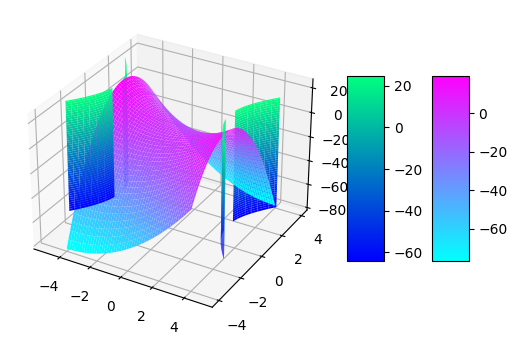
x, y = symbols('x y') z=x**2-2*x*y-4*y**2 xx=2*x**2-4*y**2-25 lagrang(z,xx)

[{l: -3/4 - I/4, x: 5*2**(1/4)*(-sqrt(2)*sqrt(2 - sqrt(2)) - sqrt(2 - sqrt(2)) - sqrt(2)*sqrt(-2 - sqrt(2)) + sqrt(-2 - sqrt(2)))/4, y: 5*2**(3/4)*sqrt(1/2 - sqrt(2)/4)/4 + 5*2**(3/4)*I*sqrt(sqrt(2)/4 + 1/2)/4}, {l: -3/4 - I/4, x: 5*2**(1/4)*(sqrt(2 - sqrt(2)) + sqrt(2)*sqrt(2 - sqrt(2)) - sqrt(-2 - sqrt(2)) + sqrt(2)*sqrt(-2 - sqrt(2)))/4, y: -5*2**(3/4)*sqrt(1/2 - sqrt(2)/4)/4 - 5*2**(3/4)*I*sqrt(sqrt(2)/4 + 1/2)/4}, {l: -3/4 + I/4, x: 5*2**(1/4)*(-sqrt(2)*sqrt(2 - sqrt(2)) - sqrt(2 - sqrt(2)) - sqrt(-2 - sqrt(2)) + sqrt(2)*sqrt(-2 - sqrt(2)))/4, y: 5*2**(3/4)*sqrt(1/2 - sqrt(2)/4)/4 - 5*2**(3/4)*I*sqrt(sqrt(2)/4 + 1/2)/4}, {l: -3/4 + I/4, x: 5*2**(1/4)*(sqrt(2 - sqrt(2)) + sqrt(2)*sqrt(2 - sqrt(2)) - sqrt(2)*sqrt(-2 - sqrt(2)) + sqrt(-2 - sqrt(2)))/4, y: -5*2**(3/4)*sqrt(1/2 - sqrt(2)/4)/4 + 5*2**(3/4)*I*sqrt(sqrt(2)/4 + 1/2)/4}]

--------------------------------------------------------------------------- TypeError Traceback (most recent call last) Cell In[33], line 4 2 z=x**2-2*x*y-4*y**2 3 xx=2*x**2-4*y**2-25 ----> 4 lagrang(z,xx) Cell In[26], line 36, in lagrang(z, xx) 34 d=Matrix([[0,fdx,fdy],[fdx,dx2,dxy],[fdy,dxy,dy2]]) 35 od=-det(d) ---> 36 if (od>0): 37 print(i+1,': Условный минимум') 38 if (od<0): File /lib/python3.11/site-packages/sympy/core/decorators.py:236, in _SympifyWrapper.make_wrapped.<locals>._func(self, other) 234 if not isinstance(other, expectedcls): 235 return retval --> 236 return func(self, other) File /lib/python3.11/site-packages/sympy/core/expr.py:371, in Expr.__gt__(self, other) 368 @sympify_return([('other', 'Expr')], NotImplemented) 369 def __gt__(self, other): 370 from .relational import StrictGreaterThan --> 371 return StrictGreaterThan(self, other) File /lib/python3.11/site-packages/sympy/core/relational.py:834, in _Inequality.__new__(cls, lhs, rhs, **options) 832 for me in (lhs, rhs): 833 if me.is_extended_real is False: --> 834 raise TypeError("Invalid comparison of non-real %s" % me) 835 if me is S.NaN: 836 raise TypeError("Invalid NaN comparison") TypeError: Invalid comparison of non-real 400*sqrt(2)*I*sqrt(-2 - sqrt(2))*sqrt(sqrt(2)/4 + 1/2) + 100*sqrt(2)*I*sqrt(-2 - sqrt(2))*sqrt(2 - sqrt(2)) + 400*sqrt(1/2 - sqrt(2)/4)*sqrt(2 - sqrt(2)) + 400*sqrt(2)*sqrt(1/2 - sqrt(2)/4)*sqrt(2 - sqrt(2)) + 400*sqrt(2)*sqrt(1/2 - sqrt(2)/4)*sqrt(sqrt(2)/4 + 1/2) - 400*I*sqrt(-2 - sqrt(2))*sqrt(sqrt(2)/4 + 1/2) - 400*sqrt(-2 - sqrt(2))*sqrt(1/2 - sqrt(2)/4) - 100*sqrt(2)*sqrt(-2 - sqrt(2))*sqrt(2 - sqrt(2)) - 400*sqrt(2)*I*sqrt(1/2 - sqrt(2)/4)*sqrt(sqrt(2)/4 + 1/2) + 400*I*sqrt(2 - sqrt(2))*sqrt(sqrt(2)/4 + 1/2) + 400*I + 400*sqrt(2)*sqrt(-2 - sqrt(2))*sqrt(1/2 - sqrt(2)/4) + 400*sqrt(2)*I*sqrt(2 - sqrt(2))*sqrt(sqrt(2)/4 + 1/2)

Упражнение С1

import matplotlib.pyplot as plt import numpy as np fig = plt.figure() xs = np.linspace(-4, 4, 50) ys = np.linspace(-4, 4, 50) X, Y = np.meshgrid(xs, ys) Z = X**2+12*X*Y+2*Y**2 sx = np.linspace(-5, 5, 100) sz = np.linspace(-100, 200, 100) XX, ZZ = np.meshgrid(sx, sz) YY = (25-4*XX**2)**(1/2) #ZZ = (XX+1)**2+YY**2 import matplotlib.pyplot as plt from matplotlib import cm import numpy as np fig, ax = plt.subplots(subplot_kw={"projection": "3d"}) # построение поверхности surf = ax.plot_surface(X, Y, Z, cmap=cm.cool, linewidth=0) surf1 = ax.plot_surface(XX, YY, ZZ, cmap=cm.winter, linewidth=0) surf2 = ax.plot_surface(XX, -YY, ZZ, cmap=cm.winter, linewidth=0) # цветовой индикатор fig.colorbar(surf, shrink=0.5, aspect=5) fig.colorbar(surf1, shrink=0.5, aspect=5) plt.show()

<Figure size 640x480 with 0 Axes>

Упражнение С2

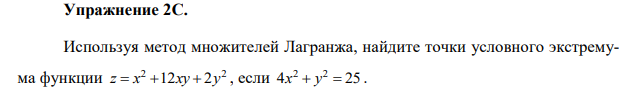
x, y = symbols('x y') z=x**2+12*x*y+2*y**2 xx=4*x**2+y**2-25 lagrang(z,xx)

[{l: -17/4, x: -3/2, y: -4}, {l: -17/4, x: 3/2, y: 4}, {l: 2, x: -2, y: 3}, {l: 2, x: 2, y: -3}] 1 : Условный максимум 2 : Условный максимум 3 : Условный минимум 4 : Условный минимум