ЛР8

import numpy as np import sympy as sp from numpy import * from sympy import * import matplotlib.pyplot as plt

Пример 1

import sympy as sp import matplotlib.pyplot as plt x = np.linspace(0, 2, 201) y = np.linspace(0, 2, 201) X, Y = np.meshgrid(x, y) Z = np.sin(np.pi * X) * np.sin(np.pi * Y) fig, ax = plt.subplots() cs = ax.contour(X, Y, Z, levels=np.linspace(-0.8, 0.8, 9)) ax.clabel(cs, cs.levels, inline=True, fontsize=10) plt.xlabel('x'); plt.ylabel('y') plt.show()

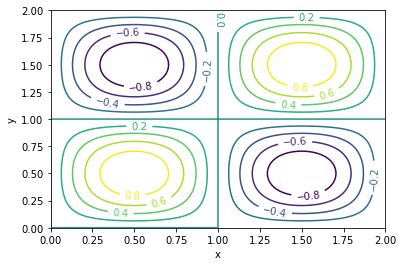
def f(t): x, y = t return np.sin(np.pi * x) * np.sin(np.pi * y)

from scipy.optimize import fmin minimum = fmin(f, np.array([1, 1]), xtol=1e-9, disp=False) print('Min:', minimum)

Min: [1.5 0.5]

minimum, f_min, _, _, _ = fmin(f, np.array([1, 1]), xtol=1e-9, disp=False, full_output=True) print('Min:', minimum) print('f:', f_min)

Min: [1.5 0.5] f: -1.0

Упражнение 1

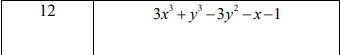
import sympy as sp import matplotlib.pyplot as plt x = np.linspace(-2, 2, 1000) y = np.linspace(-2, 3, 1000) X, Y = np.meshgrid(x, y) Z = 3*X**3+Y**3-3*Y**2-X-1 #Z = 2*X**3+X*Y**2+5*X**2+Y**2 fig, ax = plt.subplots() cs = ax.contour(X, Y, Z, levels=np.linspace(-6, 4, 15)) #ax.clabel(cs, cs.levels, inline=True) plt.xlabel('x'); plt.ylabel('y') plt.grid() plt.show()

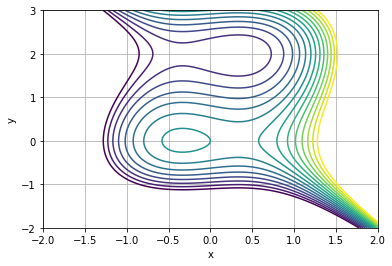
def fone(t): x, y = t return 3*x**3+y**3-3*y**2-x-1

minimum, f_min, _, _, _ = fmin(fone, np.array([1, 1]), xtol=1e-9, disp=False, full_output=True) print('Min:', minimum) print('f:', f_min)

Min: [0.33333333 2. ] f: -5.222222222222223

minimum, f_min, _, _, _ = fmin(fone, np.array([-0.5, 0]), xtol=1e-9, disp=False, full_output=True) print('Min:', minimum) print('f:', f_min)

Min: [-5.11627645e+43 9.52347084e+40] f: -4.017753263775611e+131

Упражнение 2

def proizminor(f, x0, y0): x, y = sp.symbols('x y') dx=sp.diff(f, x) dy=sp.diff(f, y) dx2=sp.diff(f, x, 2) dy2=sp.diff(f, y, 2) dxdy=sp.diff(sp.diff(f, x), y) dx=dx.subs(x, x0) dx=dx.subs(y, y0) dy=dy.subs(x, x0) dy=dy.subs(y, y0) dx2=dx2.subs(x, x0) dx2=dx2.subs(y, y0) dy2=dy2.subs(x, x0) dy2=dy2.subs(y, y0) dxdy=dxdy.subs(x, x0) dxdy=dxdy.subs(y, y0) M=Matrix([[dx2,dxdy],[dxdy,dy2]]) m=dx2 dM=det(M) print('dfdx: ', dx) print('dfdy: ', dy) print('d2fdx2: ', dx2) print('d2fdy2: ', dy2) print('dfdxdy: ', dxdy) print('минор 1: ', m) print('минор 2: ', dM)

Упражнение 3

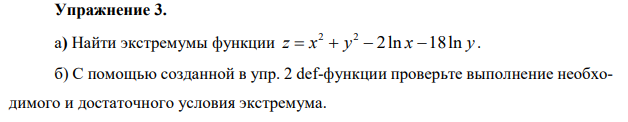
import sympy as sp import matplotlib.pyplot as plt x = np.linspace(-1, 6, 1000) y = np.linspace(-1, 6, 1000) X, Y = np.meshgrid(x, y) Z = X**2+Y**2-2*np.log(X)-18*np.log(Y) fig, ax = plt.subplots() cs = ax.contour(X, Y, Z, levels=np.linspace(-10, 6, 200)) #ax.clabel(cs, cs.levels, inline=True, fontsize=10) plt.xlabel('x'); plt.ylabel('y') plt.grid() plt.show()

C:\Users\\AppData\Local\Temp\ipykernel_10080\1906896897.py:6: RuntimeWarning: invalid value encountered in log Z = X**2+Y**2-2*np.log(X)-18*np.log(Y)

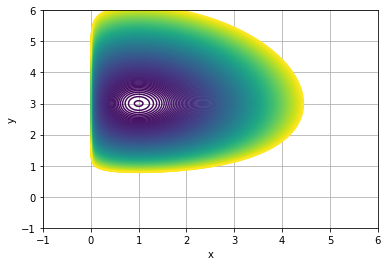
from scipy.optimize import fmin def fone(t): x, y = t return x**2+y**2-2*log(x)-18*log(y) minimum, f_min, _, _, _ = fmin(fone, np.array([1, 1]), xtol=1e-9, disp=False, full_output=True) print(minimum) print('f:', f_min)

[1. 3.00000002] f: -9.775021196025975

x, y = sp.symbols('x y') f=x**2+y**2-2*log(x)-18*log(y) x0=1 y0=3 proizminor(f, x0, y0)

dfdx: 0 dfdy: 0 d2fdx2: 4 d2fdy2: 4 dfdxdy: 0 минор 1: 4 минор 2: 16

Пример 2

import sympy as sp from sympy.abc import x, y, z df1 = x - z df2 = x - y df3 = x + z s = sp.solve([df1, df2, df3]) print(s) print(s[x])

{x: 0, y: 0, z: 0} 0

s=sp.solve([x**2+y**2-1, x-y, z-y]) print(s[0]) print(s[1]) print('x:', [sp.N(s[0][x]), sp.N(s[1][x])])

{x: -sqrt(2)/2, y: -sqrt(2)/2, z: -sqrt(2)/2} {x: sqrt(2)/2, y: sqrt(2)/2, z: sqrt(2)/2} x: [-0.707106781186548, 0.707106781186548]

Упражнение 4

def stazt(f): x, y, z = sp.symbols('x y z') dx=diff(f, x) dy=diff(f,y) dz=diff(f,z) s=solve([dx, dy, dz]) print(s) ss=size(s) dx2=diff(f,x,2) dy2=diff(f,y,2) dz2=diff(f,z,2) dxdy=sp.diff(sp.diff(f, x), y) dxdz=sp.diff(sp.diff(f, x), z) dydz=sp.diff(sp.diff(f, y), z) dx2m=ss*[0] dy2m=ss*[0] dz2m=ss*[0] dxym=ss*[0] dxzm=ss*[0] dyzm=ss*[0] for i in range(0,ss): dx2=dx2.subs(x,s[i][x]) dx2=dx2.subs(y,s[i][y]) dx2=dx2.subs(z,s[i][z]) dx2m[i]=dx2 dy2=dy2.subs(x,s[i][x]) dy2=dy2.subs(y,s[i][y]) dy2=dy2.subs(z,s[i][z]) dy2m[i]=dy2 dz2=dz2.subs(x,s[i][x]) dz2=dz2.subs(y,s[i][y]) dz2=dz2.subs(z,s[i][z]) dz2m[i]=dz2 dxdy=dxdy.subs(x,s[i][x]) dxdy=dxdy.subs(y,s[i][y]) dxdy=dxdy.subs(z,s[i][z]) dxym[i]=dxdy dxdz=dxdz.subs(x,s[i][x]) dxdz=dxdz.subs(y,s[i][y]) dxdz=dxdz.subs(z,s[i][z]) dxzm[i]=dxdz dydz=dydz.subs(x,s[i][x]) dydz=dydz.subs(y,s[i][y]) dydz=dydz.subs(z,s[i][z]) dyzm[i]=dydz m1=dx2m[i] m2=Matrix([[dx2m[i],dxym[i]],[dxym[i],dy2m[i]]]) m3=Matrix([[dx2m[i],dxym[i],dxzm[i]],[dxym[i],dy2m[i],dyzm[i]],[dxzm[i],dyzm[i],dz2m[i]]]) dm2=det(m2) dm3=det(m3) if (m1 >0 and dm2 >0 and dm3>0): print(i+1,': точка минимума') if (m1 <0 and dm2 >0 and dm3<0): print(i+1,': точка максимума') else: print(i+1,': не экстремум')

Упражнение 5

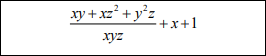
x, y, z = sp.symbols('x y z') f=(x*y+x*z**2+z*y**2)/(x*y*z)+x+1 stazt(f)

[{x: -1, y: 1, z: -1}, {x: 1, y: 1, z: 1}, {x: -I, y: -1, z: I}, {x: I, y: -1, z: -I}] 1 : точка максимума 2 : точка максимума 3 : точка максимума 4 : точка максимума

from scipy import optimize def f(x): return 256/x[0]+x[0]**2/x[1]+x[1]**2/x[2]+x[2]**2 result=optimize.brute(f,((-5,5),(-5,5),(-5,5))) print(result)

[-1.38769249e-30 -7.68818092e+00 -3.17636675e-01]

from scipy import optimize def f(x): return 256/x[0]+x[0]**2/x[1]+x[1]**2/x[2]+x[2]**2 print(optimize.differential_evolution(f,((-5,5),(-5,5),(-5,5))))

fun: -4.611686018427416e+17 message: 'Optimization terminated successfully.' nfev: 4314 nit: 93 success: True x: array([-5.55111512e-16, -4.07047969e+00, -5.89964276e-03])

from scipy import optimize def f(x): return 256/x[0]+x[0]**2/x[1]+x[1]**2/x[2]+x[2]**2 print(optimize.minimize(f,[2,2,2]))

fun: 10.349081510629931 hess_inv: array([[ 0.3842481 , 0.93769366, 0.05319554], [ 0.93769366, 3.06614485, -0.05541021], [ 0.05319554, -0.05541021, 0.14762528]]) jac: array([ -6.68950558, -9.71597195, -25.59375298]) message: 'Desired error not necessarily achieved due to precision loss.' nfev: 284 nit: 3 njev: 70 status: 2 success: False x: array([ 5.67575521, 9.02847475, -1.93728074])

x, y, z = sp.symbols('x y z') f=x+y/x+z/y+2/z stazt(f)

x, y, z = sp.symbols('x y z') f=256/x+x**2/y+y**2/z+z**2 stazt(f)