
Индивидуальное задание
![]()
x, y, dx, dy = sp.symbols('x y dx dy') f = x**3+y**3-15*x*y delx=0.1 dely=-0.2 x0=1.4 y0=1.4 teilorfirst(f, x, y, dx, dy, x0, y0, delx, dely)
dx*(3*x**2 - 15*y) + dy*(-15*x + 3*y**2) + x**3 - 15*x*y + y**3 -22.4000000000000
dx*(3*x**2 - 15*y) + dy*(-15*x + 3*y**2) + x**3 - 15*x*y + y**3
import matplotlib.pyplot as plt import numpy as np fig = plt.figure() xs = np.linspace(-6 ,6, 50) ys = np.linspace(-6, 6, 50) X, Y = np.meshgrid(xs, ys) Z = X**3+Y**3-15*X*Y ZZ = (X-1.4)*(3*x0**2 - 15*y0) + (Y-1.4)*(-15*x0 + 3*y0**2) + x0**3 - 15*x0*y0 + y0**3 import matplotlib.pyplot as plt from matplotlib import cm import numpy as np fig, ax = plt.subplots(subplot_kw={"projection": "3d"}) # построение поверхности surf = ax.plot_surface(X, Y, Z, cmap=cm.cool, linewidth=0) surf1 = ax.plot_surface(X, Y, ZZ, cmap=cm.winter, linewidth=0) # цветовой индикатор fig.colorbar(surf, shrink=0.5, aspect=5) fig.colorbar(surf1, shrink=0.5, aspect=5) plt.show()
<Figure size 640x480 with 0 Axes>
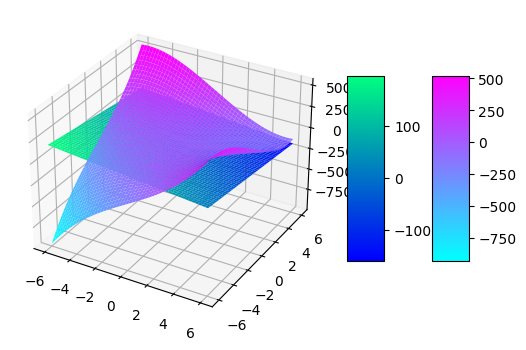
x, y, dx, dy = sp.symbols('x y dx dy') f = x**3+y**3-15*x*y delx=0.1 dely=-0.2 x0=1.4 y0=1.4 teilorsecond(f, x, y, dx, dy, x0, y0, delx, dely)
-15*dx*dy + dx*(3*x**2 - 15*y) + dy*(-15*x + 3*y**2) + x**3 - 15*x*y + y**3 -22.1000000000000
-15*dx*dy + dx*(3*x**2 - 15*y) + dy*(-15*x + 3*y**2) + x**3 - 15*x*y + y**3
import matplotlib.pyplot as plt import numpy as np fig = plt.figure() xs = np.linspace(-6, 6, 50) ys = np.linspace(-6, 6, 50) X, Y = np.meshgrid(xs, ys) Z = X**3+Y**3-15*X*Y ZZ = (X-1.4)*(3*x0**2 - 15*y0) + (Y-1.4)*(-15*x0 + 3*y0**2) + x0**3 - 15*x0*y0 + y0**3 ZZZ = -15*(X-1.4)*(Y-1.4) + (X-1.4)*(3*x0**2 - 15*y0) + (Y-1.4)*(-15*x0 + 3*y0**2) + x0**3 - 15*x0*y0 + y0**3 import matplotlib.pyplot as plt from matplotlib import cm import numpy as np fig, ax = plt.subplots(subplot_kw={"projection": "3d"}) # построение поверхности surf = ax.plot_surface(X, Y, Z, cmap=cm.cool, linewidth=0) surf1 = ax.plot_surface(X, Y, ZZ, cmap=cm.winter, linewidth=0) surf2 = ax.plot_surface(X, Y, ZZ, cmap=cm.spring, linewidth=0) # цветовой индикатор fig.colorbar(surf, shrink=0.5, aspect=5) fig.colorbar(surf1, shrink=0.5, aspect=5) fig.colorbar(surf2, shrink=0.5, aspect=5) plt.show()
<Figure size 640x480 with 0 Axes>
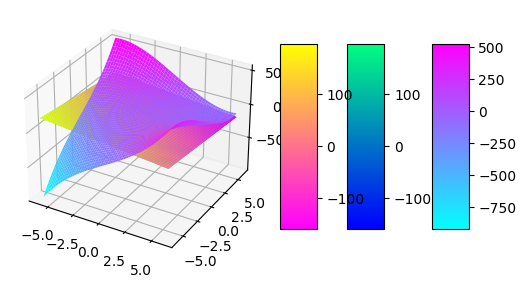
Упражнение с1

r, t, p = sp.symbols('r t p') # формулы перехода от декартовой системы координат к полярной x = r * sp.cos(t) * sp.cos(p) y = r * sp.sin(t) * sp.cos(p) zz= r * sp.sin(p) # вектор функций перехода для составления матрицы A = sp.Matrix([[x, y, zz]]) sp.pprint(A)
[r⋅cos(p)⋅cos(t) r⋅sin(t)⋅cos(p) r⋅sin(p)]
B = sp.Matrix([[sp.diff(A,r)], [sp.diff(A,t)] , [sp.diff(A,p)]]) sp.pprint(B.T)
⎡cos(p)⋅cos(t) -r⋅sin(t)⋅cos(p) -r⋅sin(p)⋅cos(t)⎤ ⎢ ⎥ ⎢sin(t)⋅cos(p) r⋅cos(p)⋅cos(t) -r⋅sin(p)⋅sin(t)⎥ ⎢ ⎥ ⎣ sin(p) 0 r⋅cos(p) ⎦
# вычисление якобиана sp.pprint(B.det()) sp.pprint(sp.simplify(B.det())) # упрощение выражения с помощью simplify
2 2 2 2 2 2 2 2 3 r ⋅sin (p)⋅sin (t)⋅cos(p) + r ⋅sin (p)⋅cos(p)⋅cos (t) + r ⋅sin (t)⋅cos (p) + r 2 3 2 ⋅cos (p)⋅cos (t) 2 r ⋅cos(p)
