Лаб. 5 КП МатАн

ЛР5

import numpy as np import sympy as sp from numpy import * from sympy import * import matplotlib.pyplot as plt

Упражнение 1

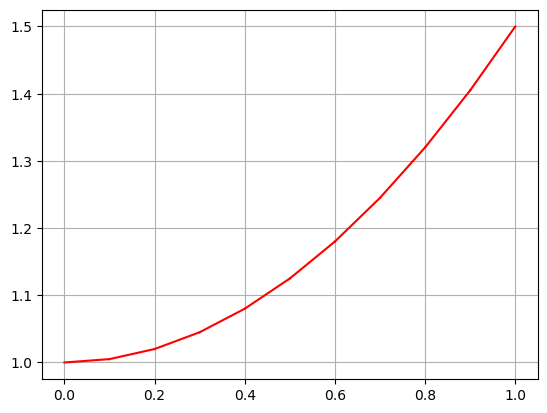
def eiler (f, x0, y0, a, b, n0, eps): x=Symbol('x') y=Symbol('y') col=['indigo','pink','cyan','orange','olive','red','yellow','black','brown','teal'] dx=(b-a)/n0 xn=zeros(n0) yn=zeros(n0) xn[0]=x0 yn[0]=y0 print('n =', n0) for i in range (1,n0+2): xn[i]=xn[i-1]+dx fsubsx=f.subs(x,xn[i-1]) ff=fsubsx.subs(y,yn[i-1]) yn[i]=yn[i-1]+ff*dx print('x =',xn[i-1],'y =',yn[i-1]) #plt.plot([xn[i-1],xn[i]],[yn[i-1],yn[i]],'-r') #plt.grid() #plt.show() print(' ') n02=2*n0 dx2=(b-a)/n02 xn2=zeros(n02) yn2=zeros(n02) xn2[0]=x0 yn2[0]=y0 z=zeros(n0) print('n =', n02) for i in range (1,n02+2): xn2[i]=xn2[i-1]+dx2 fsubsx2=f.subs(x,xn2[i-1]) ff2=fsubsx2.subs(y,yn2[i-1]) yn2[i]=yn2[i-1]+ff2*dx2 print('x=',xn2[i-1],'y=',yn2[i-1]) #plt.plot([xn2[i-1],xn2[i]],[yn2[i-1],yn2[i]],'-b') print(' ') for i in range(0,n0): for j in range (0,n02): if (xn[i]==xn2[j]): z[i]=abs(yn[i]-yn2[j]) zmax=max(z) print('max = ',zmax) print(' ') for i in range(1,n0+1): for j in range(1, n02+1): plt.plot([xn[i-1],xn[i]],[yn[i-1],yn[i]],'-m') plt.plot([xn2[j-1],xn2[j]],[yn2[j-1],yn2[j]],'-g') #plt.grid() #plt.show() n=2 w=0 while (zmax>eps): n01=n02 n02=(2+n)*n0 dx=(b-a)/n01 xn=zeros(n01) yn=zeros(n01) xn[0]=x0 yn[0]=y0 #print('n =', n01) for i in range (1,n01+2): xn[i]=xn[i-1]+dx fsubsx=f.subs(x,xn[i-1]) ff=fsubsx.subs(y,yn[i-1]) yn[i]=yn[i-1]+ff*dx #print('x=',xn[i-1],'y=',yn[i-1]) #plt.plot([xn[i-1],xn[i]],[yn[i-1],yn[i]],'-r') dx2=(b-a)/n02 #plt.grid() #plt.show() xn2=zeros(n02) yn2=zeros(n02) xn2[0]=x0 yn2[0]=y0 z=zeros(n0) print('n =', n02) for i in range (1,n02+2): xn2[i]=xn2[i-1]+dx2 fsubsx2=f.subs(x,xn2[i-1]) ff2=fsubsx2.subs(y,yn2[i-1]) yn2[i]=yn2[i-1]+ff2*dx2 print('x=',xn2[i-1],'y=',yn2[i-1]) #plt.plot([xn2[i-1],xn2[i]],[yn2[i-1],yn2[i]],'-b') print(' ') for i in range(0,n0): for j in range (0,n02): if (xn[i]==xn2[j]): z[i]=abs(yn[i]-yn2[j]) zmax=max(z) print('max = ',zmax) print(' ') for i in range(1,n0+1): for j in range(1, n02+1): #plt.plot([xn[i-1],xn[i]],[yn[i-1],yn[i]],'-r') plt.plot([xn2[j-1],xn2[j]],[yn2[j-1],yn2[j]],color=col[w]) #plt.grid() #plt.show() n+=2 w+=1 print('n = ',n*n0) plt.grid() plt.show() #subsy=f.subs(y,y0) #dd=integrate(subsy,x) #print(dd) x=linspace(0,1,1000) plt.plot(x,np.e**(x**2/2),'-r') for j in range(1, n02+1): plt.plot([xn2[j-1],xn2[j]],[yn2[j-1],yn2[j]],'-g') plt.grid() plt.show() x=Symbol('x') y=Symbol('y') f=x*y x0=0 y0=1 a=0 b=1 n0=4 eps=0.001 eiler(f,x0,y0,a,b,n0,eps)

n = 4 x = 0 y = 1 x = 0.250000000000000 y = 1 x = 0.500000000000000 y = 1.06250000000000 x = 0.750000000000000 y = 1.19531250000000 x = 1.00000000000000 y = 1.41943359375000 n = 8 x= 0 y= 1 x= 0.125000000000000 y= 1 x= 0.250000000000000 y= 1.01562500000000 x= 0.375000000000000 y= 1.04736328125000 x= 0.500000000000000 y= 1.09645843505859 x= 0.625000000000000 y= 1.16498708724976 x= 0.750000000000000 y= 1.25600170344114 x= 0.875000000000000 y= 1.37375186313875 x= 1.00000000000000 y= 1.52400597316955 max = 0.0606892034411430 n = 16 x= 0 y= 1 x= 0.0625000000000000 y= 1 x= 0.125000000000000 y= 1.00390625000000 x= 0.187500000000000 y= 1.01174926757813 x= 0.250000000000000 y= 1.02360570430756 x= 0.312500000000000 y= 1.03959954343736 x= 0.375000000000000 y= 1.05990422202012 x= 0.437500000000000 y= 1.08474572722372 x= 0.500000000000000 y= 1.11440674320249 x= 0.562500000000000 y= 1.14923195392757 x= 0.625000000000000 y= 1.18963463980784 x= 0.687500000000000 y= 1.23610474292533 x= 0.750000000000000 y= 1.28921861859790 x= 0.812500000000000 y= 1.34965074134468 x= 0.875000000000000 y= 1.41818769305359 x= 0.937500000000000 y= 1.49574483251746 x= 1.00000000000000 y= 1.58338613129778 max = 0.0125409407701227 n = 24 x= 0 y= 1 x= 0.0416666666666667 y= 1 x= 0.0833333333333333 y= 1.00173611111111 x= 0.125000000000000 y= 1.00521436149691 x= 0.166666666666667 y= 1.01044985296304 x= 0.208333333333333 y= 1.01746686583084 x= 0.250000000000000 y= 1.02629904348562 x= 0.291666666666667 y= 1.03698965852193 x= 0.333333333333333 y= 1.04959196339980 x= 0.375000000000000 y= 1.06416962955813 x= 0.416666666666667 y= 1.08079728001998 x= 0.458333333333333 y= 1.09956112168699 x= 0.500000000000000 y= 1.12055968477477 x= 0.541666666666667 y= 1.14390467820757 x= 0.583333333333333 y= 1.16972197129212 x= 0.625000000000000 y= 1.19815271364991 x= 0.666666666666667 y= 1.22935460723455 x= 0.708333333333333 y= 1.26350334632440 x= 0.750000000000000 y= 1.30079424369855 x= 0.791666666666666 y= 1.34144406381413 x= 0.833333333333333 y= 1.38569308675245 x= 0.875000000000000 y= 1.43380743004246 x= 0.916666666666666 y= 1.48608165926276 x= 0.958333333333333 y= 1.54284172263738 x= 1.00000000000000 y= 1.60444824975658 max = 0.00130811149691357 n = 32 x= 0 y= 1 x= 0.0312500000000000 y= 1 x= 0.0625000000000000 y= 1.00097656250000 x= 0.0937500000000000 y= 1.00293159484863 x= 0.125000000000000 y= 1.00586987100542 x= 0.156250000000000 y= 1.00979905018903 x= 0.187500000000000 y= 1.01472970961378 x= 0.218750000000000 y= 1.02067539150605 x= 0.250000000000000 y= 1.02765266469017 x= 0.281250000000000 y= 1.03568120113307 x= 0.312500000000000 y= 1.04478386793990 x= 0.343750000000000 y= 1.05498683540025 x= 0.375000000000000 y= 1.06631970179615 x= 0.406250000000000 y= 1.07881563580157 x= 0.437500000000000 y= 1.09251153742796 x= 0.468750000000000 y= 1.10744821860373 x= 0.500000000000000 y= 1.12367060461844 x= 0.531250000000000 y= 1.14122795781560 x= 0.562500000000000 y= 1.16017412508402 x= 0.593750000000000 y= 1.18056781087652 x= 0.625000000000000 y= 1.20247287767989 x= 0.656250000000000 y= 1.22595867607207 x= 0.687500000000000 y= 1.25110040673371 x= 0.718750000000000 y= 1.27797951703463 x= 0.750000000000000 y= 1.30668413509302 x= 0.781250000000000 y= 1.33730954450927 x= 0.812500000000000 y= 1.36995870331076 x= 0.843750000000000 y= 1.40474281101201 x= 0.875000000000000 y= 1.44178192809924 x= 0.906250000000000 y= 1.48120565269571 x= 0.937500000000000 y= 1.52315385965682 x= 0.968750000000000 y= 1.56777750788895 x= 1.00000000000000 y= 1.61523952228793 max = 0.000655509508502350 n = 32

Упражнение 2

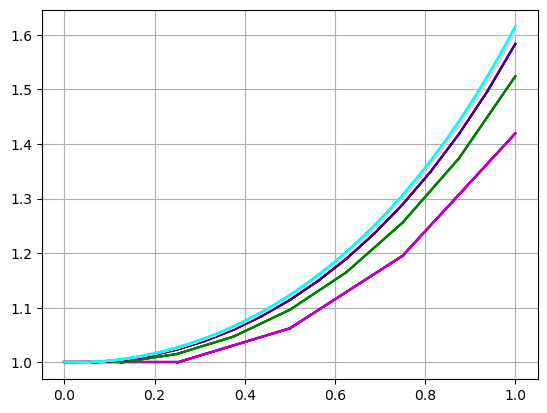
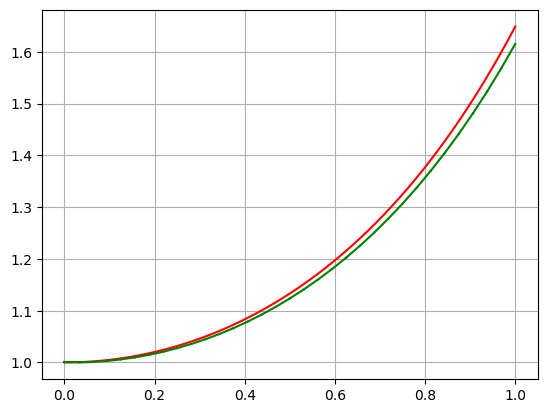
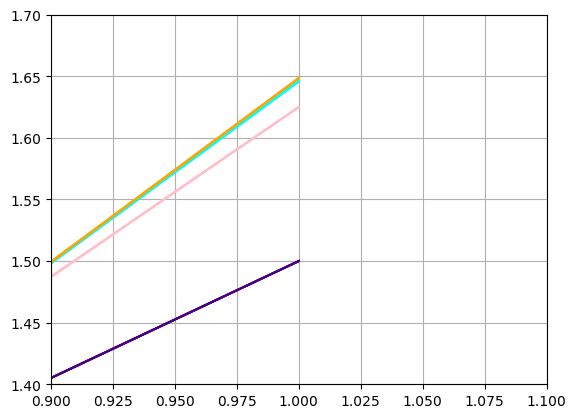
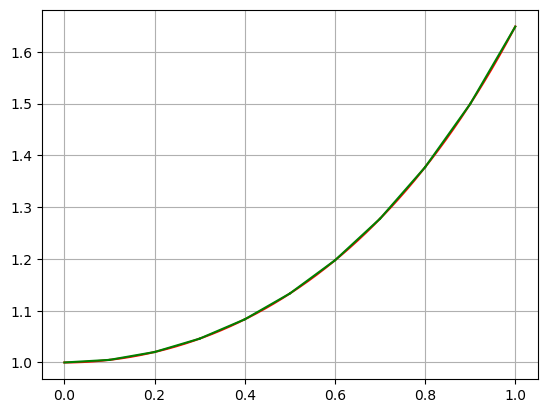
def pikara(f, x0, y0, n0): x=Symbol('x') y=Symbol('y') #t=Symbol('t') col=['indigo','pink','cyan','orange','olive','red','yellow','black','brown','teal'] phi=[0]*n0 xx=[0]*n0 phi[0]=y0 c=11 #tt=(n0-1)*zeros((c),(c)) #ty=empty((n0-1,c,c)) ty=np.zeros(((n0-1,n0-1,c))) #print(ty) #print(tt) dx=[0]*(c) print(dx) #ty=[dx]*(c) #tyy=zeros(c) #ty=[tyy]*(n0-1) #print(ty) for i in range(0,c): dx[i]=i/(c-1) print(dx) for i in range(1,n0): x=Symbol('x') fsubsy=f.subs(y,phi[i-1]) #ff2=fsubsx2.subs(y,yn2[i-1]) phi[i]=y0+integrate(fsubsy,(x,x0,x)) print(phi[i]) xx[i]=phi[i].subs(x,1) print(round(xx[i],4)) for j in range(0,n0-1): for k in range(0,c): #plt.plot(phi[i],x[j]) #for j in range(0,n0): ty[i-1,j,k]=phi[i].subs(x,dx[k]) #print(xt[i]) #plt.plot([j,j+1],[xt[i],xt[i+1]]) #print(ty) plt.grid() for k in range(1,n0): for i in range(1,n0): for j in range(1,c): plt.plot([dx[j-1],dx[j]],[ty[k-1,i-1,j-1],ty[k-1,i-1,j]],color=col[k-1]) plt.show() for k in range(1,n0): for i in range(1,n0): for j in range(1,c): plt.plot([dx[j-1],dx[j]],[ty[k-1,i-1,j-1],ty[k-1,i-1,j]],color=col[k-1]) plt.xlim([0.9,1.1]) plt.ylim([1.4,1.7]) plt.grid() plt.show() x=linspace(0,1,1000) plt.plot(x,np.e**(x**2/2),'-r') for i in range(1,c): plt.plot([dx[i-1],dx[i]],[ty[n0-2,n0-2,i-1],ty[n0-2,n0-2,i]],'-g') plt.grid() plt.show() x=Symbol('x') y=Symbol('y') f=y*x x0=0 y0=1 n0=5 pikara(f,x0,y0,n0)

[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0] [0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0] x**2/2 + 1 1.5000 x**4/8 + x**2/2 + 1 1.6250 x**6/48 + x**4/8 + x**2/2 + 1 1.6458 x**8/384 + x**6/48 + x**4/8 + x**2/2 + 1 1.6484

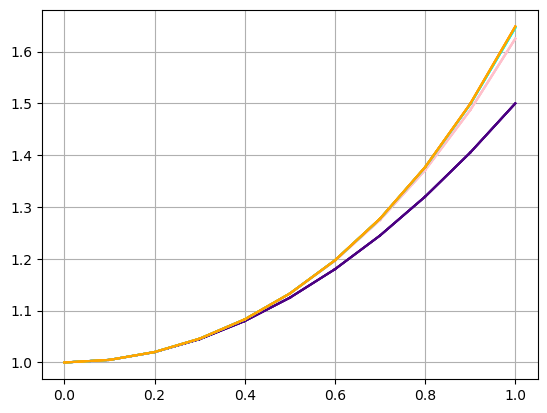
def pikara(f, x0, y0, n0): x=Symbol('x') y=Symbol('y') #t=Symbol('t') phi=[0]*n0 xx=[0]*n0 phi[0]=y0 c=11 #tt=(n0-1)*zeros((c),(c)) #ty=empty((n0-1,c,c)) #ty=np.zeros(((n0-1,c,c))) #print(ty) #print(tt) dx=[0]*(c) #ty=[dx]*(c) #tyy=zeros(c) ty=np.zeros((n0-1,c)) #print(ty) for i in range(0,c): dx[i]=i/(c-1) print(dx) for i in range(1,n0): x=Symbol('x') fsubsy=f.subs(y,phi[i-1]) #ff2=fsubsx2.subs(y,yn2[i-1]) phi[i]=phi[i-1]+integrate(fsubsy,(x,x0,x)) print(phi[i]) xx[i]=phi[i].subs(x,1) print(round(xx[i],4)) for j in range(0,n0-1): for k in range(0,c): #plt.plot(phi[i],x[j]) #for j in range(0,n0): ty[j,k]=phi[i].subs(x,dx[k]) #print(xt[i]) #plt.plot([j,j+1],[xt[i],xt[i+1]]) print(ty) for i in range(1,n0): for j in range(1,c): plt.plot([dx[j-1],dx[j]],[ty[i-1,j-1],ty[i-1,j]],'-r') plt.grid() plt.show() x=Symbol('x') y=Symbol('y') f=y*x x0=0 y0=1 n0=2 pikara(f,x0,y0,n0)

[0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0] x**2/2 + 1 1.5000 [[1. 1.005 1.02 1.045 1.08 1.125 1.18 1.245 1.32 1.405 1.5 ]]