ЛР3

import numpy as np import sympy as sp from numpy import * from sympy import * import matplotlib.pyplot as plt

Упражнение 1

def chsum (a, n): s=0 for i in range (1,n+1,1): s=s+a.subs(x,i) plt.plot(i,s,'*') plt.grid() plt.show() x=Symbol('x') a0=1/x n0=200 chsum(a0, n0)

Упражнение 2

def ssum (a, n, nn): e=0.001 s=0 ss=0 for i in range (1,n+1,1): s+=a.subs(x,i) for j in range (1,nn+1,1): ss+=a.subs(x,j) print(round(ss,5)) print(" ") print(round(s,5)) print(" ") S=np.abs(ss-s) print(round(S,5)) if S<=e: print("Ряд сходится") else: print("Ряд расходится") x=Symbol('x') n0=200 n1=100 ssum(0.5**x, n0, n1)

1.00000000000000 1.00000000000000 0 Ряд сходится

chsum(0.5**x, n0)

ssum(1**x, n0, n1)

100 200 100 Ряд расходится

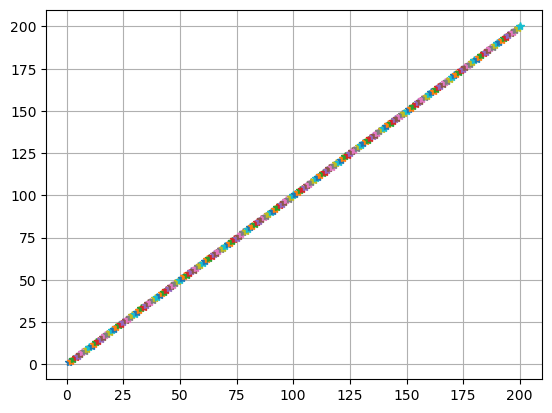
chsum(1**x, n0)

ssum(5**x, 8, 5)

3905 488280 484375 Ряд расходится

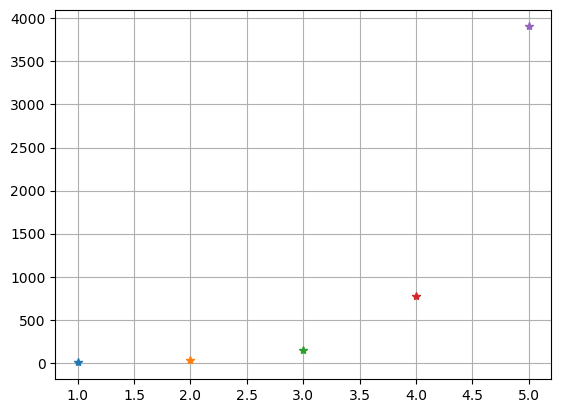
chsum(5**x, 5)

Упражнение 3

ssum(x**(-0.5), n0, n1)

18.58960 26.85926 8.26965 Ряд расходится

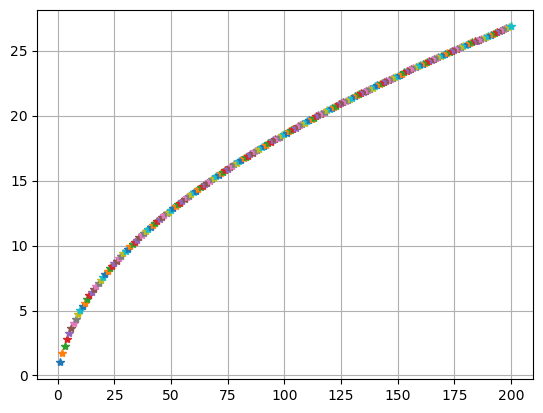
chsum(x**(-0.5), n0)

ssum(x**(-1), n0, n1)

5.18738 5.87803 0.69065 Ряд расходится

chsum(x**(-1), n0)

ssum(x**(-2), n0+50, n0)

1.63995 1.64094 0.0010 Ряд сходится

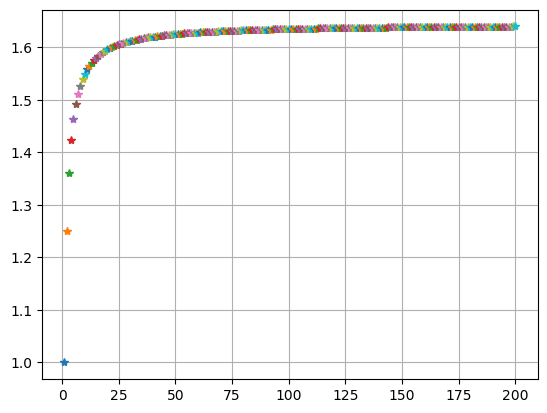
chsum(x**(-2), n0)

Упражнение 4

n=Symbol('n') lim1=sp.limit(1/n,n,sp.oo) #lim2=sp.limit(5**n,n,sp.oo) lim3=sp.limit(sqrt(n**3)/(n**2+n+12),n,sp.oo) lim4=sp.limit((sqrt(n)+n)/(n**2),n,sp.oo) print(lim1) #print(lim2) print(lim3) print(lim4)

0 0 0

def asum (a, n): s=0 b=0 for i in range (1,n+1,1): s=s+a.subs(x,i) b=a.subs(x,i) plt.plot(i,s,'*b') plt.plot(i,b,'*r') plt.grid() plt.show() x=Symbol('x') a0=1/x n0=200 asum(a0, n0)

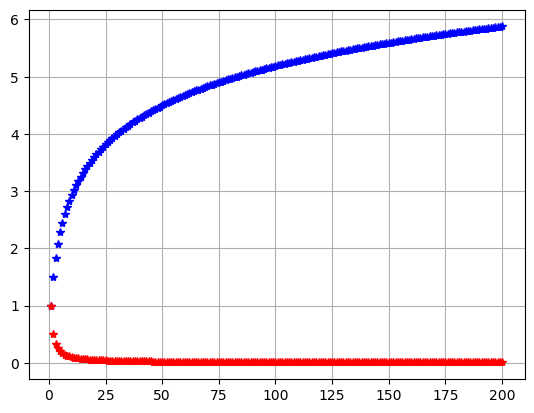
a0=sqrt(x**3)/(x**2+x+12) asum(a0, n0)

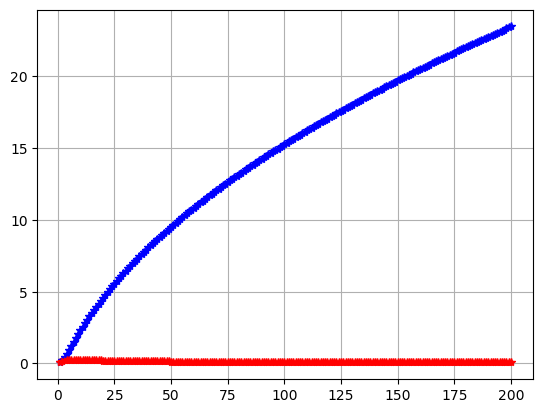
a0=(sqrt(x)+x)/(x**2) asum(a0, n0)

Упражнение 5

a0=(sqrt(x)+x)/(x**2)+1/x chsum(a0,n0)

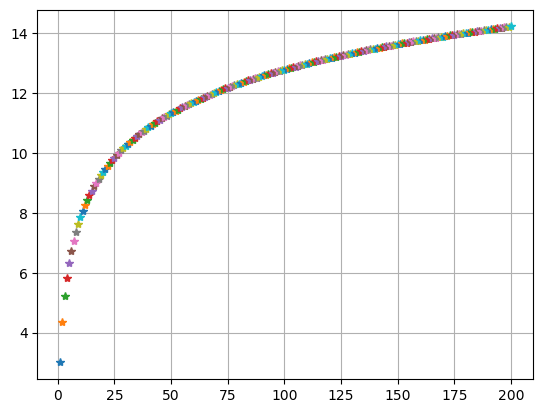
a0=x/factorial(x)+0.5**x chsum(a0,n0)

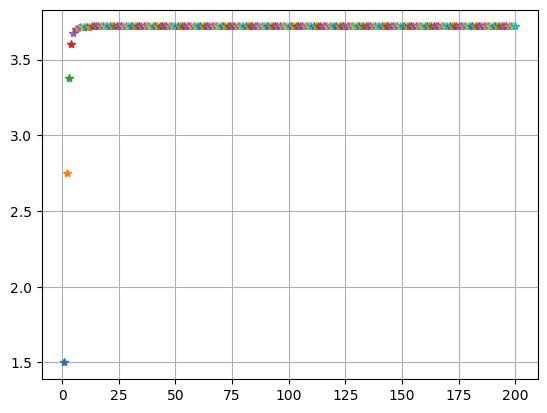
Упражнение 6

def chssum (a, b, n): s=0 z=0 for i in range (1,n+1,1): s=s+a.subs(x,i) z=z+b.subs(x,i) plt.plot(i,s,'*r') plt.plot(i,z,'*b') plt.grid() plt.show() x=Symbol('x') a0=1/(x*sqrt(x+1)*sqrt(x+2)) b0=5/x**2 n0=200 chssum(a0, b0, n0)

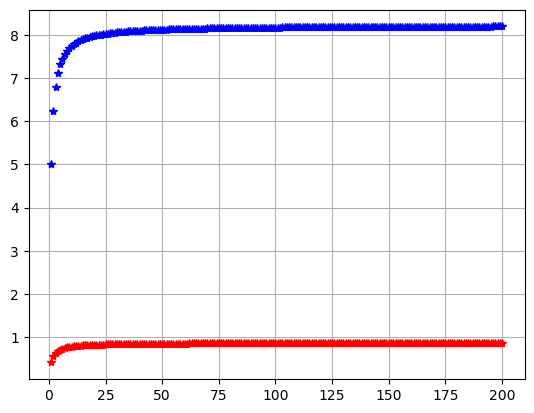
def assum (a, b, n): s=0 z=0 for i in range (1,n+1,1): s=a.subs(x,i) z=b.subs(x,i) plt.plot(i,s,'*r') plt.plot(i,z,'*b') plt.grid() plt.show() x=Symbol('x') a0=1/(x*sqrt(x+1)*sqrt(x+2)) b0=5/x**2 b0 n0=30 assum(a0, b0, n0)

a0=(2+sin(x))/sqrt(x) b0=2/x**1 n0=200 chssum(a0, b0, n0)

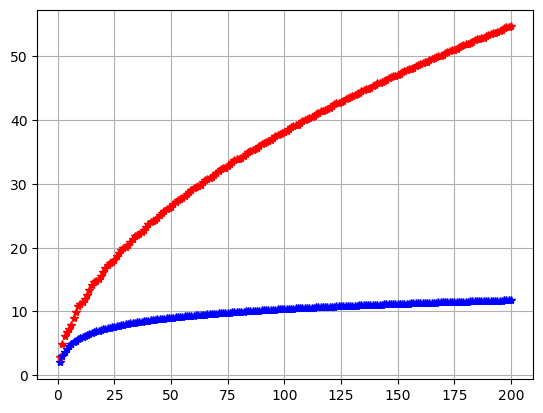
a0=(2+sin(x))/sqrt(x) b0=2/x**1 n0=20 assum(a0, b0, n0)

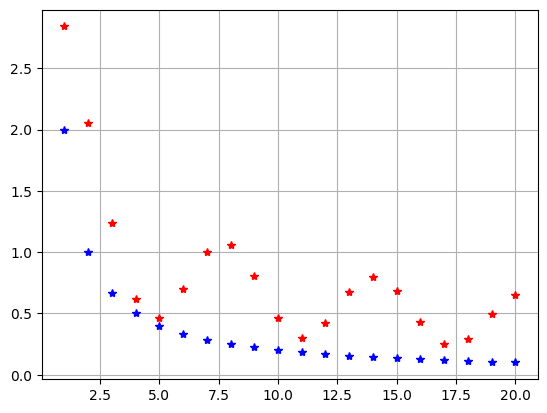
Упражнение 7

#def rsum (a, e): # N=1 # y=a.subs(x,N) # while (y>=e): # s=s+a.subs(x,N) # y=a.subs(x,N) # N+=1 # print(N) # print(round(s,2)) #x=Symbol('x') #a0=(x+5)/3**x #e0=0.005 #rsum(a0, e0)

def orad (a, e): s=0 N=1 y=a.subs(x,N) y1=a.subs(x,N+1) q=y1/y while (q>=1): s=s+a.subs(x,N) y=a.subs(x,N) y1=a.subs(x,N+1) q=y1/y N+=1 r=y1/(1-q) while (r>e): s=s+a.subs(x,N) y=a.subs(x,N) y1=a.subs(x,N+1) q=y1/y r=y1/(1-q) N+=1 print(N) print(round(s,2)) x=Symbol('x') a0=(x+5)/3**x e0=0.005 orad(a0, e0)

8 3.25

Упражнение 8

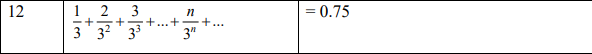
a0=x/3**x e0=0.001 #rsum(a0, e0) orad(a0, e0)

9 0.75

Упражненеи 9

def orada (a, e): s=0 N=1 y=a.subs(x,N) y1=a.subs(x,N+1) q=y1/y while (q>=1): s=s+a.subs(x,N) y=a.subs(x,N) y1=a.subs(x,N+1) q=y1/y N+=1 r=np.abs(y1/(1-q)) while (r>e): s=s+a.subs(x,N) y=a.subs(x,N) y1=a.subs(x,N+1) q=y1/y r=np.abs(y1/(1-q)) N+=1 print(N) print(round(s,2)) x=Symbol('x') a0=(-1)**(x-1)/(3**x-1) e0=0.001 orada(a0, e0)

7 0.40

Упражнение 10

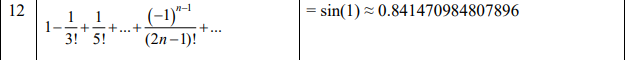
x=Symbol('x') a0=(-1)**(x-1)/factorial(2*x-1) e0=0.001 orada(a0, e0)

4 0.84